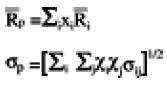
DISCUSIÓN SOBRE LA TEORÍA MODERNA DEL PORTAFOLIO. APLICACIÓN DE LA INTERNACIONALIZACIÓN DEL PORTAFOLIO, INCLUYENDO EL CASO COLOMBIANO
OSCAR DANIEL MEJÍA CARVAJAL
Noveno semestre de Economía y Negocios Internacionales E-mail:oscmejia@hotmail.com
RESUMEN
El análisis se realiza en el marco del modelo desarrollado por Markowitz en 1952, Modern Portfolio Theory (MPT), el cual en esencia muestra la manera de lograr el máximo rendimiento posible de un portafolio, dado un nivel determinado de riesgo, e indica las ventajas de una apropiada diversificación del portafolio.
El período analizado corresponde a la última década del siglo XX, la cual estuvo marcada en Colombia con variaciones importantes en el desempeño económico del país, y al mismo tiempo, con cambios notables en la importancia e institucionalidad del mercado de valores. No obstante lo anterior, el mercado de valores colombiano continúa caracterizándose por su precariedad. En efecto, la capitalización global del mercado representa únicamente el 13% del PIB, muy por debajo del nivel de otros países latinoamericanos.i
Por otro lado, la economía norteamericana mostró ininterrumpidamente en el mismo período un nivel de crecimiento sin precedentes, al mismo tiempo que los desarrollos tecnológicos en las áreas de comunicación y computación permitieron masificar e internacionalizar aún más el mercado de valores.
La aplicación del modelo de Markowitz debe brindar herramientas para el análisis del riesgo y toma de decisiones de inversión condicionada al grado de aversión al riesgo del inversor.
El documento finaliza con una comparación real, partiendo de una inversión supuesta en carteras nacionales e internacionales.
PALABRAS CLAVE
Frontera eficiente, teoría moderna de portafolios, riesgo sistemático.
Clasificación: B
SUMMARY
The analysis is similar in framework to the model developed by Markowitz in 1952, known as Modern Portfolio Theory (MPT). This model basically shows how to extract the maximum possible yield from a portfolio, given a certain level of risk, and also highlights the advantages of a properly diversified portfolio.
The time frame of the analysis corresponds to the final decade of the 20th century, a period that in Colombia was marked by large fluctuations in the country´s economic performance, as well as by important changes in the structure of its stock markets. Despite this restructuring, however, the present state of Colombia´s stock markets continues to be precarious. Their total capitalization barely -13% of the country´s Gross Domestic Product- is far below the level of other countries in Latin America.
The US economy, meanwhile, enjoyed a period of unprecedented growth during the same period, white technological change in the fields of communication and information technology enabled the country´s financial markets to achieve even further growth both at home and abroad.
The application of Markowitz´s model provides handy tools for risk analysis and decision-making in accordance with the individual investor´s risk tolerance.
The article concludes with a performancecomparison of domestic and international portfolios.
KEY WORDS
Efficient frontier, modern portfolio theory, systematic risk
Clasification: B
EL MODELO DE MARKOWITZ
El modelo, plantea la solución para encontrar las proporciones de una inversión que debe usarse para maximizar la rentabilidad a un nivel deseado de riesgo, o el equivalente, minimizar el riesgo a un grado de renta deseado.
El modelo utiliza datos históricos para hacer los cálculos necesarios, lo que abre un interrogante adicional: ¿Cuál debe ser el horizonte temporal apropiado para que los resultados sean los más consistentes posibles? Aunque no está formalizada matemáticamente esta pieza del modelo, lo aconsejable es mirar el largo plazo, donde la tendencia de los mercados puede identificarse, pues no se reflejan tan marcadamente las grandes fluctuaciones que el mercado tiene en el corto plazo, y usar un horizonte temporal acorde con el tiempo destinado para la inversión.
Aunque por lo general las inversiones en papeles no se hacen a muy corto plazo (entre otras razones por los costos de transacción), quien lo hace así tomaría medidas de partida engañosas si mirara un horizonte temporal muy amplio (los datos con los que el modelo trabaja, históricos), pues este inversor necesita usar la tendencia que tengan los mercados en un período menor, el corto plazo, por lo tanto el modelo no es aplicable a ellos.
Este modelo usa el concepto de diversificación en forma implícita, pues en él se pretende encontrar una solución que tenga unos retornos mayores al retorno del activo menos rentable y menor al retorno del activo que tenga un rendimiento mayor, esto si se considera que no existe la posibilidad de que los inversores tomen posiciones cortas, o sea vender activos, porque especulan de forma bajista sobre ellos.
El riesgo sistemático es el mismo riesgo del mercado, este se ve afectado por los acontecimientos macroeconómicos, de orden público, civil y demás, que cambien las percepciones de los consumidores sobre el rumbo de la economía. Los mercados de cada país (o mundiales), no son más que el reflejo de lo que piensan los consumidores (los cuales hacen posible su existencia). Si los consumidores creen que se encuentran en un país solvente y con buenas expectativas de crecimiento, sin costos inflacionarios de consideración, muy seguramente (exceptuando situaciones coyunturales y/o variables adicionales, y/o específicas, que causen el efecto contrario) los mercados tendrán una tendencia positiva. Por lo tanto, entre más diversificado esté un portafolio su riesgo sistemático será menor, y aún más si la diversificación es internacional, siguiendo la idea de que los acontecimientos que influyan en un país del cual la cartera posee papeles, pueden no tener efecto sobre los otros países, o mejor aún, los acontecimientos negativos de un país pueden dar como resultado efectos positivos en otros. El riesgo sistemático nunca podrá desaparecer, pues es el riesgo que tiene la economía, el riesgo de cada papel, es el riesgo que éste tiene más el riesgo sistemático del mercado del país en el que se encuentra, por lo tanto, mientras más activos tenga un portafolio, el riesgo tenderá a parecerse al riesgo sistemático, el cual siempre es menor que el de cualquier portafolio.
Las variables claves del modelo son la rentabilidad de los activos y el riesgo de cada uno de estos. El riesgo son las variaciones que pueden tener los rendimientos de una inversión. Por ejemplo, los bonos del Tesoro que tienen una prima establecida e inamovible la cual es pactada antes de la compra, son activos de los que se tiene certeza de su rentabilidad, o sea, ni variabilidad ni incertidumbre sobre cuál será la cuantía de las pérdidas o ganancias, o en otras palabras, tiene una medida de riesgo igual a cero.
Para medir el riesgo se usa la desviación estándar, la cual nos indica qué tan dispersos están los datos históricos de sus respectivas medidas muestrales; entre más dispersos estén los datos es más posible que el activo fluctúe, ya sea hacia arriba o hacia abajo, lo cual es incertidumbre para el inversor y se traduce en forma de mayor riesgo. Es necesario tener en cuenta que el riesgo guarda una relación directa con la rentabilidad, porque no tendría sentido para ningún inversor racional, comprar un activo con la misma rentabilidad que otro, pero con una mayor medida de riesgo, o viceversa, un activo con el mismo nivel de riesgo que otro, pero con una rentabilidad menor.
Para medir el riesgo de la cartera es necesario añadir otro elemento que estime la relación entre los papeles, la correlación, la cual mide la relación que tienen los cambios de uno de los activos con respecto a otro. Un portafolio ideal, desde el punto de vista de la óptima cobertura, de por ejemplo dos activos, tendría una correlación de -1 (ρ= -1), lo cual haría que los cambios en sentido negativo de uno de los papeles produjera cambios en sentido positivo en el otro, y que al medir el retorno de la cartera fuera positivo, dependiendo de la combinación de cada uno de los activos que se hayan seleccionado.
Este modelo no arroja una única respuesta, dado que existen diferentes tipos de inversores, agresivos, neutrales y adversos, con respecto al riesgo, pero sí encuentra el portafolio con las combinaciones exactas de cada activo que lo conforma que para determinado nivel de rentabilidad esperada determinada minimiza el riesgo. Esto se logra mediante un proceso de optimización de la función objetivo. El conjunto de portafolio que tiene un nivel de rentabilidad cualquiera y mínimo riesgo conforma la frontera eficiente, como ya se mencionó. Ninguna otra combinación por debajo de la frontera es válida para los inversores racionales. Como medida adicional proporcionada por el modelo se encuentra una línea tangente a la frontera eficiente, que parte del eje de los retornos. El punto de la frontera eficiente, que es tangente a esta línea, indica la combinación óptima entre los papeles y un activo sin riesgo como lo son las letras del Tesoro. De ese punto en adelante, y dependiendo del nivel de tolerancia que tenga cada inversor al riesgo, se desplaza sobre la frontera eficiente, ya sea en busca de un nivel de rentabilidad esperado, o hacia un punto de riesgo (desviación estándar) deseado.
Con este modelo, Markowitz demostró que el desempeño de papeles como acciones está afectado por diferentes fuerzas económicas como las tasas de interés, tasas de cambio y otras variables; y que el riesgo del portafolio no depende sólo de las desviaciones estándar de cada uno de los activos, sino también del número de activos que éste contenga, pues como se mencionó, a medida que el número de papeles de un portafolio tiende a ser igual al número de papeles en el mercado, el riesgo del portafolio tenderá a ser igual al riesgo del mercado, o en otras palabras, el riesgo del portafolio tenderá a aproximarse al riesgo sistemático del mercado, lo cual es un punto más de apoyo a la diversificación internacional.
Para resolver el modelo de Markowitz, es necesario maximizar el ratio θ. En términos matemáticos:
Max θ =[Rp - Rf ]/σp
Donde Rp es la tasa esperada de rentabilidad del portafolio, y σp es la desviación estándar de los retornos del portafolio.
La rentabilidad del portafolio y la desviación estándar se calculan de la siguiente manera:
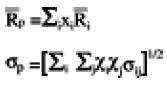
APLICACIONES DEL MODELO
La práctica financiera en general ha encontrado que el modelo de Markowitz es particularmente útil para determinar la composición de un portafolio en términos de las clases generales de activos que el mismo pueda tener, por ejemplo, acciones de un mercado emergente y acciones de un mercado desarrollado, y es mucho menos práctico cuando se trata de balancear un portafolio compuesto de activos de una misma clase. La razón fundamental radica en el esfuerzo computacional y estadístico que implica el análisis de un número grande de activos. La aplicación del modelo a un portafolio de 200 acciones, por ejemplo, significa calcular 200 rentabilidades y 19.900 covarianzas.
En un contexto como el de Colombia, resulta muy interesante ver la influencia de un activo nacional, por la situación coyuntural, sobre un portafolio internacional; en un razonamiento a priori se podría pensar que incluir activos colombianos en un portafolio diversificado internacionalmente lo beneficiaría si la covarianza con otros activos es negativa; esta es una de las razones por la cual la diversificación internacional es un mecanismo para la disminución del riesgo sistemático de cada país.
Una vez desarrollado el modelo será determinado qué tan beneficioso o perjudicial es incluir activos de este país en portafolios con activos pertenecientes a países desarrollados, a mercados con más fluidez y profundidad que las del nuestro. Para tales fines es necesario encontrar la frontera eficiente de los activos, o sea, el conjunto de combinaciones de las proporciones del capital de la inversión en cada uno de los activos y los retornos y nivel de riesgo de cada combinación para la cartera. Su importancia radica en el hecho de que una vez encontrado, podemos decidir con un criterio más estructurado sobre qué cartera es mejor que otra, dada la relación directa entre riesgo y retorno, ya que entre mayor sea el riesgo que corre el capital, mayores retornos exigirá cualquier inversor racional.
DESARROLLO
Los datos estadísticos
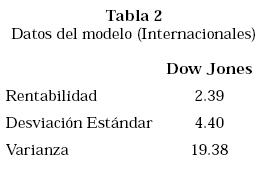
Para la aplicación del modelo al caso colombiano se tomó para el portafolio de instrumentos domésticos -el portafolio nacional- el conjunto de acciones colombianas representadas por el Índice de la Bolsa de Bogotá (IBB), y para el portafolio ampliado -el portafolio internacional- el conjunto de acciones norteamericanas representadas por el Índice Norteamericano Dow Jones.
Los índices no son más que un reflejo de los precios de las acciones tomadas globalmente, y son el mejor indicador de los movimientos de las bolsas. El cálculo se realiza mediante algún procedimiento de ponderación, generalmente tomando la participación ponderada de cada acción en la respectiva bolsa.
La utilización de los índices generales del mercado presenta la ventaja que considera globalmente todas las acciones de la bolsa, en la proporción que aparezcan en el índice, y evita la selección puntual de acciones específicas. Sin embargo, presenta la desventaja que toma en cuenta los dividendos de las acciones, los cuales generalmente son muy pequeños en relación con la rentabilidad que se obtiene por medio de las ganancias de capital.
Los datos estadísticos cubren prácticamente la última década del siglo XX, lo que permite intentar medir la capacidad predicativa del modelo, al comparar los resultados con los primeros años de la siguiente década. El período analizado de casi una década es suficiente para determinar la tendencia del mercado, y servir de base a una decisión de inversión. Es de recordar que los datos históricos no son el mejor estimador del futuro, pero este es uno de los supuestos de los cuales parte el modelo.
EL PORTAFOLIO NACIONAL
El Mercado de Acciones en Colombia
Antecedentes
La inestabilidad de los mercados financieros y la necesidad de manejar profesionalmente los crecientes fondos de inversión, que aumentan a medida que se incrementa el grado de profundización financiera de los países, han implicado últimamente la utilización generalizada de las herramientas modernas de gestión de portafolios, cuyos conceptos básicos fueron establecidos por Harry Markowitz, en su trabajo seminal presentado hace medio siglo. Esa utilización se ha intensificado debido a los adelantos tecnológicos más recientes en materia computacional, al aumento de capacidad de procesamiento de datos a todos los niveles, y a la disponibilidad de información.
La necesidad de manejar los portafolios de inversión, y las demás operaciones financieras de una manera más profesional y moderna es aún más sentida en países en desarrollo como Colombia, donde existe gran inestabilidad de las variables económicas y es relativamente reducida la disponibilidad de datos financieros, tanto micro como macroeconómicamente. Lo anterior hace más compleja la toma de decisiones de inversión; sin embargo no ha estimulado la investigación y la aplicación generalizada de esas herramientas en Colombia, no obstante que el modelo fue formalizado en 1952 por Harry Markowitz, y desde esa fecha se ha refinado considerablemente y ha ampliado sus posibilidades de aplicación.
El mercado de acciones en Colombia continúa siendo bastante precario, no obstante que en los últimos años han existido esfuerzos puntuales encaminados a mejorar su posición relativa dentro de las posibilidades de inversión de los inversionistas, tanto nacionales como extranjeros.
Algunas de las acciones encaminadas hacia ese objetivo son las siguientes:
No obstante que el tamaño del mercado continúa siendo muy pequeño, el interés de los inversionistas por el mercado de acciones aumentó en los noventa, y el mercado mismo presenció un importante crecimiento, al mismo tiempo que los precios obtuvieron un repunte sin precedentes.
Como se puede apreciar en la Gráfica 1, del índice de la bolsa de Bogotá,ii ésta traía un crecimiento sostenido desde principios de la década, con algunas fluctuaciones en sentido negativo, pero la tendencia global era bastante positiva, tanto así que llegó muy cerca de los 1.500 puntos básicos a finales de 1997. Como es conocido, la bolsa refleja muchos de los acontecimientos macroeconómicos de cada país, por lo tanto, es razonable atribuir esta tendencia positiva a fenómenos como la apertura económica, que hicieron que nuestro país comenzara a competir con las empresas de los países desarrollados, y ampliara sus mercados al mundo. Este es un proceso que todavía no ha terminado de ser asimilado completamente por la economía. El crecimiento de la bolsa fue muy vigoroso y con una marcada tendencia hasta octubre de 1997, año que fue muy negativo, pues el ya posesionado presidente de la república Ernesto Samper, y el deterioro de sus relaciones con Estados Unidos frenaron este desarrollo. Fuera de esto, en ese año (2 de julio de 1997) comenzó la crisis asiática, con la vertiginosa devaluación de sus monedas con respecto al dólarii, principalmente causada por tener un sistema financiero doméstico pero con libres flujos de capital y la influencia del sensible mercado cambiario. Lo cual al mercado cambiario colombiano, en el que intervino el Banco de la República subiendo los tipos de interés para defender la banda cambiaria, le ocasionó una disminución de la inversión tanto doméstica como extranjera, que posiblemente llevó al inicio de la recesión del país, el cual se encontraba en un momento de bonanza para las mafias, que ocasionaba grandes inyecciones de dólares al mercado. Por lo tanto, desde octubre de 1997 la tendencia es marcadamente a la baja.
La crisis que se vive desde 1997 ha venido acompañada de desempleo, el cual ha tomado valores muy considerables en el entorno latinoamericano: alrededor del 12% (en promedio). Los valores más altos se encuentran en los períodos más recientes. Uno de los sectores más sólidos de la economía era el de la construcción, el cual en el final de la década no volvió a mostrar desempeño.iii
La situación de orden público del país, por la guerrilla, ha sido un factor decisivo en esta recesión, la zona de distensión crea un ambiente de inseguridad y tensión para las personas, empresas e inversores en general, haciéndolos considerar la viabilidad de invertir capital en Colombia.
Factores como el anterior, entre otros, han ocasionado que los flujos de capitales hacia el exterior lleven a la economía a un grado de liquidez tal, que el aparato financiero colapsará.
El riesgo país, medido por agencias internacionalesiv ha crecido considerablemente para Colombia, dando herramientas concretas a los inversores para rechazar ideas de inversión.
El mercado monetario
Normalmente en economías poco desarrolladas financieramente, el mercado monetario, que corresponde a los instrumentos financieros de menos de un año, tiende a ser el más líquido y el más desarrollado. Colombia no es la excepción. En efecto, el mercado de corto plazo representa una proporción muy alta del mercado financiero, tanto en términos del ahorro financiero, como de los volúmenes transados en las bolsas de valores. Los instrumentos principales de dicho mercado son los títulos del Tesoro, los certificados de depósito a término y los pactos de retroventa y retrocompra, que funcionan principalmente en el ámbito institucional. Por la naturaleza de los instrumentos financieros de este mercado, el mercado monetario tiende a ser bastante estable.
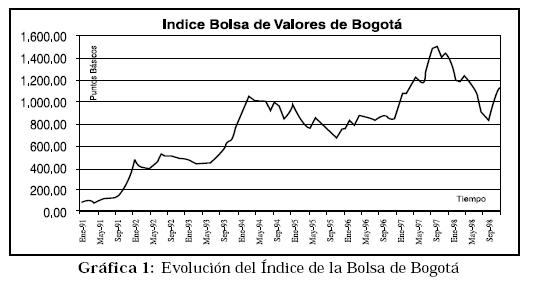
En el período analizado, el rendimiento de los CDT se caracterizó por tasas bastante elevadas, con algunos movimientos significativos en el mediano plazo, pero con mucha gradualidad en los movimientos mismos. El retorno se situó alrededor del 22%, pero con bastante estabilidad, medida en términos de la varianza de los rendimientos (Ver Gráfica 2).
LA FRONTERA EFICIENTE
El portafolio nacional se configura con dos clases de activos, un instrumento del mercado monetario, los CDT, y un instrumento del mercado de capitales, las acciones representadas por el índice de la Bolsa de Valores de Bogotá.
La Tabla 1 ilustra los datos requeridos por el modelo de Markowitz para estimar la frontera eficiente.
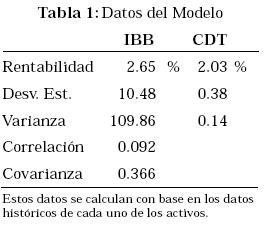
Como se puede apreciar, se mantiene la relación fundamental, y directa, entre la rentabilidad y el riesgo (desviación estándar), el IBB tiene una mayor rentabilidad pero es castigado con un riesgo mucho mayor que el de los CDT (10.48 > 0.38). Es claro que por las pocas fluctuaciones de los CDT en el interés, tiene una desviación casi tan pequeña como los activos sin riesgo.
Comparativamente, el rendimiento de las acciones es ligeramente más alto que el de los CDT. Sin embargo la volatilidad es considerablemente más alta. La correlación entre los dos activos es un poco mayor que cero, lo cual no representa un problema en sí mismo, pero el modelo enseña que hay una mayor efectividad entre mayor (con signo negativo, que tienda a -1) sea la correlación entre los dos activos.
Usando los procedimientos matemáticos del modelo y partiendo de los datos de la Tabla 1 se calculan la rentabilidad y las desviaciones estándares para cada combinación posible de las proporciones de cada uno de los dos activos, acciones y CDT, lo cual al graficarlo en un diagrama de dispersión nos muestra la frontera eficiente, los ejes son la desviación estándar (eje x), y los retornos (eje Y), del portafolio. La frontera eficiente representa el conjunto de carteras, para cada nivel de riesgo que no tiene una combinación mejor. Cualquier cartera por debajo de la frontera eficiente representa una combinación que no es la óptima, desde el punto de vista que no es racional tener una combinación de activos con igual riesgo que otra pero con menos rentabilidad esperada. Si queremos que el modelo no permita posiciones cortas, todos los valores de las proporciones deben ser positivos, los extremos de la gráfica representarán cada uno (sólo en el caso de dos activos), la desviación y la rentabilidad de cada uno de los activos que la conforman (Ver Gráfica 3).
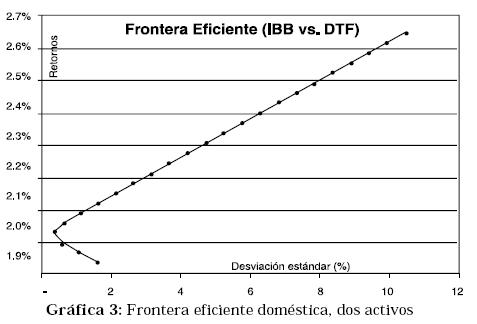
Como se puede apreciar en la gráfica, cada inversor, dependiendo del nivel de riesgo que quiera tener en su cartera, escogerá la combinación de las proporciones de cada uno de los activos que la conforman, la cual se encuentra sobre la frontera eficiente. Lo más importante a considerar es que los inversores sólo se moverán sobre la frontera eficiente, o sea sobre las combinaciones que cada punto significa. Esta decisión dependerá básicamente de cuánto está dispuesto a arriesgar el inversor, o análogamente, de cuánto espera que la cartera le rente.
PORTAFOLIO INTERNACIONAL
El mercado de acciones en Estados Unidos
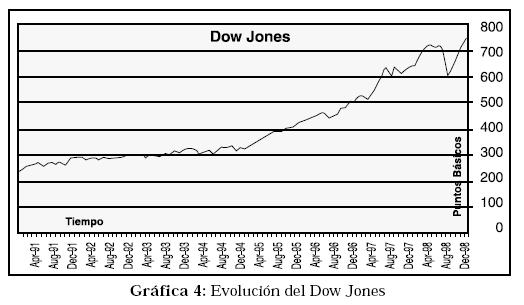
Uno de los índices (posiblemente el más conocido) usados para medir el desempeño de la bolsa de Valores de Nueva York es el Dow Jones; este, al igual que todos los índices de las bolsas dan una idea a los inversores de en qué sentido se mueven los mercados, y qué tan pronunciadas son las fluctuaciones. Como se aprecia en la gráfica de evolución del Dow Jones, para la década en estudio ha estado muy estable, con una tendencia muy positiva, posiblemente inducida por los grandes desarrollos tecnológicos que desde esta década y hasta nuestros días ha liderado Estados Unidos (Ver Gráfica 4).
La frontera eficiente del mercado internacional
La diversificación internacional es la forma más eficiente de obtener portafolios óptimos, debido a la posible poca relación que tienen los acontecimientos de un país sobre otros. Básicamente, la idea es buscar papeles de diferentes mercados que no tengan relación entre sí, lo cual puede proporcionar una cartera cubierta, y no que con cualquier externalidad en uno de los países se vengan abajo todos los activos.
El riesgo sistemático de los mercados internacionales es menor que el riesgo sistemático de los mercados domésticos de cada país, por lo tanto, entre más activos diversificados internacionalmente tenga un portafolio, su riesgo tenderá a ser igual al riesgo sistemático del mercado internacional.
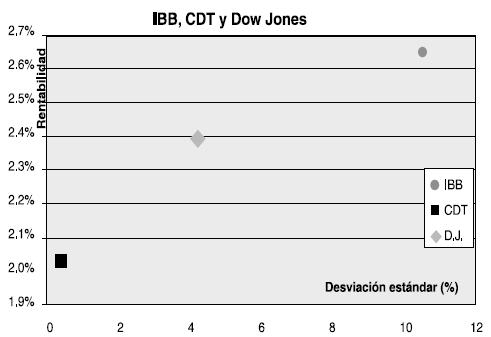
Retomando la cartera compuesta por dos activos, IBB y CDT y buscando ver el efecto de la diversificación internacional para un portafolio doméstico colombiano real, se conforma un nuevo portafolio internacional, compuesto por IBB, CDT colombianos y el Dow Jones. La finalidad es ver el efecto sobre el portafolio inicial al diversificarlo internacionalmente.
El resultado de esta combinación de tres activos diversificados internacionalmente, es la siguiente frontera eficiente de la Gráfica 5.
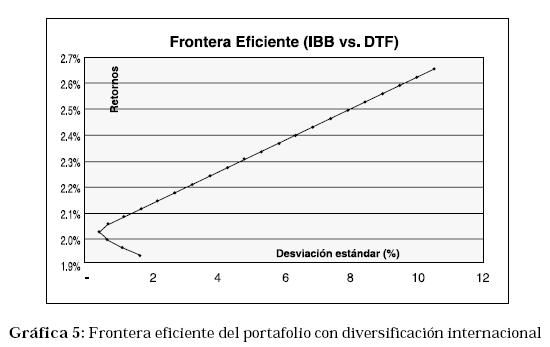
Como ya se ha mencionado, esta gráfica representa al conjunto de rentabilidades y desviaciones estándar óptimas, que tiene cada combinación de los tres activos.
Comparación de las fronteras
A continuación, se presenta una gráfica comparativa entre la frontera eficiente con diversificación doméstica y la frontera eficiente con diversificación internacional (Ver Gráfica 6).
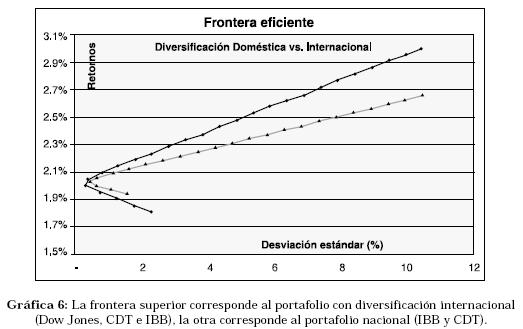
Como se puede apreciar claramente, la diversificación internacional agrega efectos de valiosa importancia a un portafolio. Esto se debe a que el portafolio, al diversificarse internacionalmente, disminuye el riesgo sistemático inherente (el riesgo del país), y asume el riesgo sistemático internacional. Claro está que para que el riesgo del portafolios sea muy cercano al del mercado internacional debe tener un gran número de papeles.
Por ejemplo, si invirtiendo en el portafolio nacional queremos que éste rente 2.5%, el riesgo del portafolio será 7.97% (en la frontera eficiente, línea delgada con triángulos) pero si se invierte en el portafolio internacional en busca de la misma rentabilidad de 2.5% dicho portafolio corresponde a un riesgo de 4.84% (en la frontera eficiente, línea gruesa con puntos), mucho menor que el equivalente al nacional para este mismo nivel de rentabilidad esperada.
Por lo tanto, el hecho de que la frontera eficiente de portafolio diversificado internacionalmente se encuentre por encima de la frontera eficiente con diversificación doméstica, proporciona una gran ventaja a los inversores.
En la gráfica 6 se puede apreciar la relación que existe entre el riesgo y las rentabilidades de cada uno de los tres activos. Como se puede observar, entre más riesgo tiene cada uno de ellos, ofrece un mayor nivel de retornos. Esta relación fundamental es de vital importancia por el hecho de que puede conllevar a la toma de decisiones no óptimas si es omitida su consideración.
Hacer el cálculo de la frontera eficiente para dos activos es relativamente sencillo usando una computadora: hallar los retornos y las desviaciones estándar para las posibles combinaciones de los dos activos; por ejemplo, si se calculan las combinaciones partiendo de invertir 100% en uno de los activos y 0% en el otro, y haciendo cambios de por ejemplo 1% entre ellos hasta invertir 0% en el primero y 100% en el segundo, daría como resultado 100 datos de rentabilidad y 100 datos de desviaciones estándar, los cuales al ser graficados forman la frontera eficiente entre ellos, pero cuando el número de papeles es superior a dos, el número de cálculos aumenta considerablemente; para hacer este cálculo se usó un proceso de optimización de matrices, con el cual se simplifica la tarea.
CAPACIDAD PREDICTIVA DEL MODELO
Ahora, con el fin de mostrar qué tan acertado puede llegar a ser el modelo, se escogerá el portafolio indicado para un determinado inversor, con un nivel de aceptación de riesgo puntual. Después se mirará cómo es el desempeño de ese portafolio con el paso del tiempo, si fuese comprado el 1o. de enero de 2000 y el horizonte de la inversión es un año y medio, hasta junio de 2001.
Determinación del portafolio óptimo
Desde un punto de vista teórico, la determinación del portafolio óptimo implica la maximización de la utilidad esperada del inversionista. Esto requiere conocer los niveles de utilidad de cada una de las relaciones entre riesgo y retorno. Siguiendo el análisis macroeconómico clásico, las curvas de indiferencia son utilizadas para ilustrar la relación anteriormente indicada, y existe un marco matemático que permite obtener el punto óptimo, que no es otro que el punto tangente entre la frontera tangente y la curva de indiferencia en el espacio riesgo - retorno. Sin embargo, aunque el aspecto teórico es bastante claro, y por lo demás elegante, desde el punto de vista práctico su aplicación es extremadamente compleja, por la dificultad que implica la determinación de las curvas de indiferencia del inversionista.
Existen algunas aproximaciones al problema, sin embargo la práctica financiera utiliza un procedimiento más intuitivo, tomando las decisiones de inversión basadas en las probabilidades de pérdida o las probabilidades de fallar en lograr un determinado nivel objetivo de rentabilidad. Si se asume que los retornos son normalmente distribuidos, un supuesto que es fácilmente verificable en la práctica, es simple transformar los parámetros de rentabilidad y riesgo a un marco de probabilidad de pérdida, tal como se ilustra en la Tabla 3.
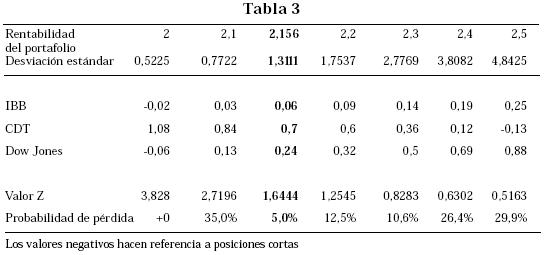
Por ejemplo, un inversionista con expectativas de una rentabilidad mensual de 2.4%, debe aceptar una desviación estándar de 3.8082, lo cual en un escenario de distribución normal implica una probabilidad de pérdida de 26.4%.
Por lo tanto, si se quiere tener un porcentaje de pérdida de 5%, se puede esperar una rentabilidad mensual de 2.156% y una desviación estándar de 1.3111.
Si se supone que el inversor tiene disponibles 100 millones de pesos, usando el modelo, con un nivel de riesgo de pérdida de 5%, invertiría en cada activo las siguientes sumas:
IBB: $ 6.264.390 (6.2%)
CDT: $ 70.144.518 (70.2%)
Dow Jones: $ 23.591.092 (23.6%)
Los datos relacionados con cada activo a la fecha del 1o. de enero de 2000 y su respectiva evolución son los que aparecen en la Tabla 4. Allí se aprecia cómo fue el desarrollo de cada uno de los activos que conforman el portafolio internacional, mes a mes.
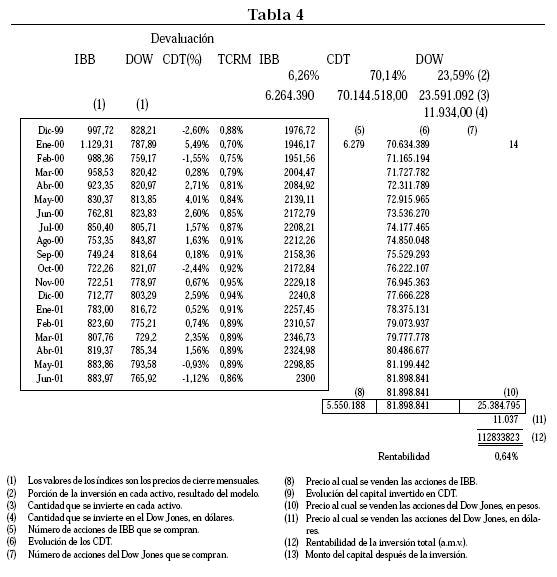
Comparación histórica
La Tabla 4, muestra que tanto el IBB como el Dow Jones cerraron, con respecto a la compra, a un valor menor; estos dos activos conformaban el 88,48%, sin embargo ésta no arrojó pérdidas de capital debido a que casi el 70% del portafolio que estaba invertido por fuera de Colombia (en Estados Unidos) se vio beneficiado por la devaluación del peso frente al dólar, y esto conllevó a que así los puntos básicos del Dow Jones fueran menores, y aunque generara pérdidas se lograra una utilidad por concepto de devaluación, al ser cuantificada en pesos.
La meta era invertir en una cartera que rentara 2.4%, y como aparece en la Tabla 4 se obtuvo un 2,68%. Como los datos que analiza el modelo al inicio, ya consideraban el efecto compuesto de la devaluación sobre los activos extranjeros, se puede decir que el modelo es un buen predictor de carteras.
Es claro que el modelo no da la fórmula para no perder nunca usando la diversificación, pero sí proporciona una herramienta para la toma de decisiones de inversión en carteras, con un proceso estructurado.
CONCLUSIONES
Como el anterior, pueden realizarse muchos portafolios y analizar su evolución con el paso del tiempo, y sería erróneo llegar a la conclusión de que el modelo no funciona si en algunas de las carteras que se conformen no tiene resultados positivos, dado que éstas se verán afectadas por factores económicos de diversas índoles, y que pueden cambiar la percepción de los consumidores sobre su economía y de esta forma afectar los mercados bursátiles y demás activos.
Los datos históricos, que son la base del modelo, no son los mejores predictores del futuro, y debido a esta imperfección los resultados pueden verse afectados por tendencias del pasado que pueden llegar a no tener ninguna relación con el futuro. Por lo tanto, el horizonte temporal que debe ser tenido en cuenta debe ser lo suficientemente amplio para evitar hacer predicciones basadas en una fluctuación de la economía causada por una externalidad.
BIBLIOGRAFÍA
CHEOL S. Eun y BRUCE G. Resnick. International Financial Management. 2da edición. España: McGraw Hill. Capítulo 2, pp. 48-52. 1997.
JAMES L. FARRELL, Jr., Portfolio Management, Segunda edición. USA: McGraw Hill. Capítulo 1-4. 1997
ELTON, E.J. & GRUBER, M.J. Modern Portfolio Theory and lnvestment Analysis. John Wiley & Sons; 6th Edition edition. 11 Sep 2002
LINCON L. Chao. Estadística. Colombia: McGraw Hill, tercera edición. 1993
DOCUMENTOS DE LA WEB (SITIOS DE REFERENCIA EN LAS NOTAS FINALES)
i Banco Mundial, sección de datos estadísticos, mercados mundiales, www.worldbank.org
ii Datos históricos obtenidos de la Superintendencia de Valores de Colombia. Los datos se encuentran en períodos diarios.
iii Publicado por el Departamento de Planeación Nacional, www.dane.gov.co. Standard & Poor.
iv International Financial Management, McGraw Hill, Segunda Edición, Cheol S. Eun y Bruce G. Resnick Capítulo 2, páginas 48-52, 1997