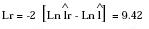CARACTERÍSTICAS
SOCIOECONÓMICAS
Y CONSISTENCIA
EN LA TOMA DE DECISIONES*
JOHN JAMES MORA
Economista, Universidad del Valle, Maestría Universidad Autónoma de Madrid, Jefe del
Departamento de Economía, Universidad Icesi.
email: jjmora@icesi.edu.co
*Este artículo es el resultado de la investigación "La paradoja de ALLAIS en los estudiantes de Economía de
la Universidad Icesi" financiado por la Facultad de Ciencias Administrativas y Económicas de la Icesi, y
contó con la ayuda de la estudiante Sayuri P. Tamura. Agradezco los comentarios de los participantes a las
presentaciones de las investigaciones realizadas en el 2001 en el Departamento de Economía de la Icesi,
así como los comentarios de Harvy Vivas de la Universidad del Valle y de un evaluador anónimo. De igual
forma, se agradecen los comentarios a la versión que circuló en la serie Borradores de Economía y Finanzas
de la Universidad Icesi. Los errores que persisten son de mi absoluta responsabilidad.
RESUMEN
Este ensayo analiza cuál es el efecto
de las características socioeconómicas
sobre la consistencia en las preferencias
cuando los agentes se encuentran
eligiendo entre loterías. El
análisis parte de realizar la prueba
de ALLAIS, sobre la consistencia en las
elecciones, a los estudiantes de la
carrera de Economía y Negocios Internacionales
de la Universidad Icesi
y, se encuentra que el sexo, el estrato
socioeconómico, el ingreso, la
edad y el semestre en forma conjunta
no son relevantes para explicar la
consistencia en las preferencias. Sin
embargo, también se observa que la
edad y el semestre podrían ayudar a
explicar la consistencia.
SUMMARY
This essay analyzes the effects of social
and economic characteristics on
the consistency of the preferences.
The analysis begins with an Allais
Test on the consistency of choices
made by students of Economics and
International Business. It is found
that sex, social and economic level,
income, age and level of course work
jointly are insufficient to explain the
consistency of preferences. Nonetheless,
the age of the student and his
level of course work do provide a partial explanation of the observed consistency.
JEL Classification: C91, D81
KEY WORDS:
Allais paradoxes, Probit models,
Principal components.
1. INTRODUCCIÓN
Una forma de analizar la toma de
decisiones, en condiciones de incertidumbre,
consiste en usar la Teoría de
la Utilidad Esperada(en adelante
TUES), desarrollada por John von
Neumann y Oskar Morgenstern.
Hacia 1952, Maurice ALLAIS presentó
dos trabajos criticando el poder
descriptivo de la TUES, a través de
mostrar violaciones sistemáticas de
la misma. Desde que ALLAIS estableció
estas violaciones se ha repetido un
sinnúmero de veces la prueba de
ALLAIS, comprobando que existe inconsistencia
en las elecciones de los
individuos.
A raíz de los trabajos sobre consistencia,
en la década de los noventa se desarrollaron
versiones estocásticas de
la TUES [Starmer (2000)]. En este
nuevo camino, la TUES se convierte
en estocástica al asignarle un término
aleatorio de error. Los trabajos de
Hey y Orme (1994), Loomes y Sugden
(1995) y Hey (1996) muestran cómo
modelar TUES estocásticas.
Este ensayo sigue la tradición de la
TUES estocástica, sólo que a diferencia
de los trabajos anteriores aquí se
explorará qué tan relevante será el
vector de características socioeconómicas
para explicar una TUES estocástica.
Al igual que los trabajos sobre
la TUES estocástica, los individuos
actúan satisfaciendo sus preferencias
de acuerdo con las restricciones de la
teoría de la utilidad esperada aunque
pueden cometer errores en su elección,
los cuales pueden surgir de muchas
formas según Hey (1995).2
2. LA TEORÍA DE LA UTILIDAD
ESPERADA
Defínase a A, B y C como loterías y p
una probabilidad. Una mixtura "probabilística"
de las loterías se denotará
como pA + (1-p)B, p 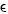 [0,1]. Una
serie de resultados específicos serán
loterías degeneradas con probabilidad
de uno. Denótese la relación "A
es al menos tan buena como
B" a A
[0,1]. Una
serie de resultados específicos serán
loterías degeneradas con probabilidad
de uno. Denótese la relación "A
es al menos tan buena como
B" a A 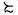 B, la relación "A preferido a
B" como A
B, la relación "A preferido a
B" como A  B y la relación "A indiferente
a B" como A
B y la relación "A indiferente
a B" como A  B. Los siguientes
axiomas sobre las preferencias deben
cumplirse:
B. Los siguientes
axiomas sobre las preferencias deben
cumplirse:
- Ordenamiento: Las preferencias
son completas ( A
 B, B
B, B  A o A
A o A  B) y se cumple la transitividad
(si A
B) y se cumple la transitividad
(si A  B y B
B y B  C
C 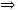 A
A  C).
C).
- Continuidad: La relación de preferencias
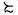 sobre el espacio de
loterías simples, ⁄ , es continua si
para A, B y C, donde A
sobre el espacio de
loterías simples, ⁄ , es continua si
para A, B y C, donde A  B
B  C ,
existe un único p tal que pA +
(1-p)C
C ,
existe un único p tal que pA +
(1-p)C 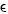 B.3
B.3
- Independencia: La relación de
preferencias
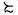 sobre el espacio de
las loterías, ⁄ , satisface el axioma
de la independencia si para
todo A, B, C
sobre el espacio de
las loterías, ⁄ , satisface el axioma
de la independencia si para
todo A, B, C 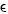 ⁄ y p
⁄ y p 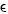 (0,1) A
(0,1) A 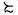 B si
y solo si pA + (1-p)C
B si
y solo si pA + (1-p)C 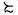 pB+ (1-p)C.
pB+ (1-p)C.
Los axiomas implican que las preferencias pueden representarse usando un
índice de utilidad numérico. La utilidad de un juego se construye como la utilidad
esperada de los posibles resultados para una lotería discreta, con varios
resultados xi, cada uno con probabilidad de suceso pi. A continuación, para cada
x 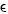 X asigne un valor de utilidad μ(xi) al resultado xi.
X asigne un valor de utilidad μ(xi) al resultado xi.
Defínase, para la lotería L 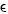 ⁄ : L= (p1,....,pn), la función de utilidad esperada
como
⁄ : L= (p1,....,pn), la función de utilidad esperada
como

Esta función de utilidad esperada es separable en los premios y
lineal en las probabilidades.
3. LA CONSISTENCIA EN LAS PREFERENCIAS
Suponga el siguiente conjunto de elecciones:
Lotería A: $100.000 con una probabilidad del 80% ó $10.000 con una probabilidad
del 20%.
Lotería B: $200.000 con una probabilidad del 60% ó $10.000 con una probabilidad
del 40%.
A continuación elija una de las siguientes loterías:
Lotería C: $100.000 con una probabilidad del 40% ó $10.000 con una probabilidad
del 60%.
Lotería D: $200.000 con una probabilidad del 30% ó $10.000 con una probabilidad
del 70%.
Suponga que un individuo tiene el patrón de elección A  B, entonces deberá
cumplirse que C
B, entonces deberá
cumplirse que C  D. Veamos por qué: Dado que A
D. Veamos por qué: Dado que A  B entonces:
B entonces:
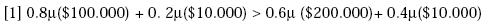
Y, si C  D entonces:
D entonces:
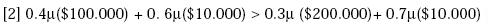
La demostración de por qué si A  B entonces deberá cumplirse que
C
B entonces deberá cumplirse que
C  D consiste en que [2] es una transformación de [1]. De esta forma, si [1]
se cumple [2] también deberá cumplirse debido al axioma de independencia:4
D consiste en que [2] es una transformación de [1]. De esta forma, si [1]
se cumple [2] también deberá cumplirse debido al axioma de independencia:4
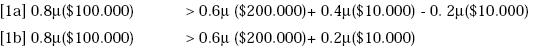
Multiplicando por 0.5 a ambos lados:
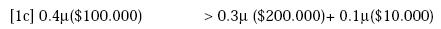
Y, sumando 0.6μ($10.000) a ambos lados se obtiene:
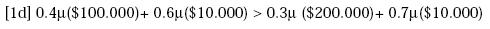
De esta forma, una prueba que pregunte
sobre la consistencia en las
elecciones deberá mostrar que si estas
son consistentes A  B y deberá
cumplirse que C
B y deberá
cumplirse que C  D ya que [1d] es
igual a [2].5 Formalmente, la consistencia
en la TUES se puede definir
como sigue: Sea p > q, X3 > X2 > X1 y 0
< λ < 1. A continuación, suponga el
siguiente conjunto de elecciones:
D ya que [1d] es
igual a [2].5 Formalmente, la consistencia
en la TUES se puede definir
como sigue: Sea p > q, X3 > X2 > X1 y 0
< λ < 1. A continuación, suponga el
siguiente conjunto de elecciones:
Condición 1: Los sujetos eligen entre:
Lotería A: X2 con probabilidad p y X1
con probabilidad ( 1 - p ).
Lotería B: X3 con probabilidad q y X1
con probabilidad ( 1 - q ).
Condición 2: Los sujetos eligen entre:
Lotería C: X2 con probabilidad λp y
X1 con probabilidad ( 1 - λp ).
Lotería D: X3 con probabilidad λq y
X1 con probabilidad ( 1 - λq ).
Observe la igualdad entre prob ( X2 ) / prob ( X3) en A vs. B y en C vs. D. Es
claro nuevamente, que un individuo
deberá preferir A y C en tanto:
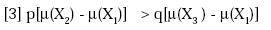
Y, deberá preferir B y D si:
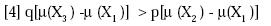
4. EL EFECTO DE LAS
CARACTERÍSTICAS
SOCIOECONÓMICAS
EN LA CONSISTENCIA
Durante los últimos años se ha cuestionado
la versión determinística de
la TUES. En particular, el hecho de que
los individuos actúen sobre preferencias
fijas y no cometan errores en sus
elecciones. De esta forma, si la teoría
es interpretada literalmente no sobrevivirá
a ningún análisis pues una sola
observación es suficiente para refutar
la misma.
Los trabajos de Harless y Camerer(
1994) y Hey y Orme(1994) incorporan un término de error que busca
incorporar aleatoriedad en la TUES,
aunque sus resultados no son concluyentes
pues por un lado Hey y
Orme(1994) encuentran que la TUES
en su versión estocástica es tan buena
como cualquier otra teoría para
modelar las elecciones de los individuos,
mientras que Harless y Camerer(
1994) usando diferentes procesos
estocásticos muestran que las violaciones
sistemáticas de la TUES son
robustas.6
Sin embargo, los trabajos realizados
hasta ahora no han investigado si una
especificación estocástica de la TUES
puede ser explicada por factores socioeconómicos.
Esta idea será explorada
a continuación.
Sea Vη la valoración de una acción η,
en la cual se cumple que un individuo
prefiera A a B, es decir p [μ(X2)-
μ(X1)] - q[μ(X3 ) - μ(X1 )] > 0. Sea Vω
una valoración ω que cumple las mismas
condiciones cuando C es preferido
a D. Observe que si Vη > 0 entonces
se cumple que A es preferido a B
y, si Vω > 0 entonces se cumple que C
es preferido a D.
No es difícil mostrar que, para valores
apropiados de p, q y λ, si el individuo
prefiere A a B entonces Vη =
p[μ(X2) - μ (X1) - q[μ (X3) - μ(X1)] > 0 y
si prefiere C a D entonces Vω = λp[μ
(X2) - μ(X1)] - λq[μ(X3) - μ(X1)] > 0. De
esta forma, cuando hay consistencia en
las preferencias, se cumple que
A  B y C
B y C  D. Por lo cual:
D. Por lo cual:
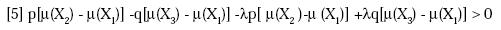
Dado que p > q y 0 < λ < 1 cuando el
comportamiento es consistente con la
TUES [5] será positivo. A continuación,
defínase la variable Cηω siempre que el
sujeto sea consistente. Es decir, en el
caso de un individuo cuyas preferencias
sean A  B y C
B y C  D tendremos:
D tendremos:
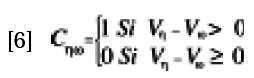
Ahora, defínase una función estocástica
p(•,•) la cual asigna una probabilidad
en el intervalo (0,1) a la acción
Cηω y sea Prob(Cηω) la probabilidad de
que Cηω sea elegido. Si la consistencia
en las preferencias es explicada por un
vector de Características Socioeconómicas
W, entonces:
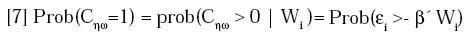
Sea Cηω* la valoración crítica de decisión
según la TUES tal que si Cηω >
Cηω* el individuo es consistente con sus
preferencias.7 Asuma que Cηω* es una
variable aleatoria distribuida en forma
normal, de modo que la probabilidad de que Cηω* sea menor que ( o
igual a) Cηω pueda calcularse a partir
de la siguiente función de probabilidad
normal acumulativa estandarizada:
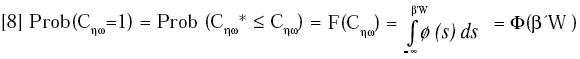
Donde s es una variable aleatoria que
viene distribuida en forma normal con
media cero y varianza unitaria. Si los
βi son iguales a cero entonces la consistencia
en las preferencias no puede
explicarse por el vector de características socioeconómicas. Por el contrario,
si los βi son diferentes de cero
entonces la consistencia y, por ende
las elecciones, pueden ser explicadas
en forma estocástica por las características
socioeconómicas.
5. RESULTADOS
En la prueba participaron 221 estudiantes
de la carrera de Economía y
Negocios Internacionales de la Icesi.8
Con el fin de comprobar si la versión
estocástica de la TUES es explicada por
un vector de características socioeconómicas,
y usando el programa LIMDEP
7.0, se estimó la ecuación [8] cuyos resultados
fueron los siguientes:
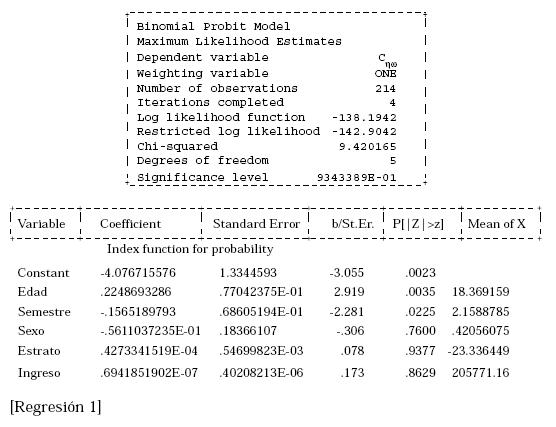
En la regresión (1) la variable dependiente
es la consistencia en las preferencias,
Cηω, y como variables independientes
se encuentran la edad,
el semestre, el tipo de sexo, el estrato
socioeconómico y el ingreso. De estas
variables, las únicas significativas
al 95% fueron la edad y el semestre.
La prueba Lr muestra un valor
de 9.42 y la X2(5) al 95% es 11.07 y al
99% es 12.83 por lo cual no se puede
rechazar la hipótesis de que conjuntamente
los coeficientes sean cero.9
Con el fin de analizar sí existe algún
tipo de estructura en los datos se procedió
a realizar un análisis de componentes
principales, usando como
variable de clasificación la consistencia
en las preferencias. Los resultados
encontrados fueron:
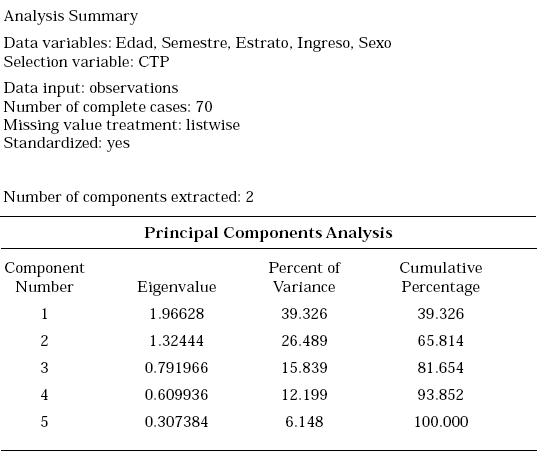
Siguiendo el criterio de Kaiser(1960)
se retienen solamente aquellos componentes
cuyas raíces características
sean mayores que 1. De acuerdo con
este criterio existen solamente dos
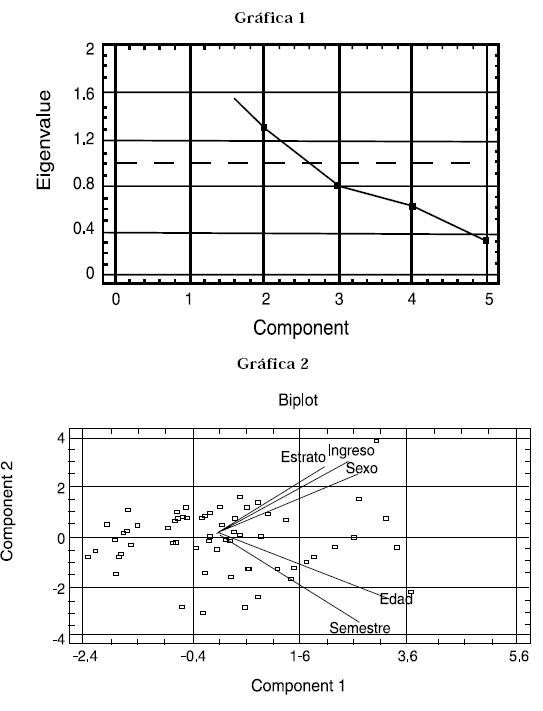
componentes de clasificación. Según
el criterio del test de Scree (Gráfica
2) propuesto por Cattel (1966) también
existen dos componentes: Uno
cuyas variables son la edad y el semestre
y otro cuyas variables son el
sexo, el estrato y el ingreso. Esto se
puede observar en el siguiente conjunto
de gráficas:
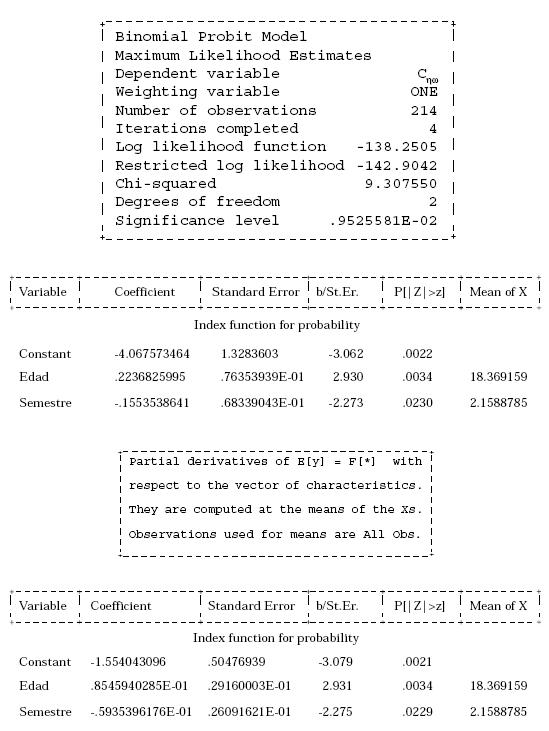
Como puede observarse, la prueba Lr
muestra un valor de 9.30 y la X2(2) al
95% es 5.99 y al 99% es 9.21, por lo
cual, se puede rechazar la hipótesis
de que conjuntamente los coeficientes son iguales a cero. Dado que la t-Student al 95% es de 1.645 y al 97.5%
es de 1.96 los parámetros son significativos.
Los resultados son interesantes pues
muestran que a mayor edad existe
una mayor consistencia en las preferencias
y a mayor semestre disminuye
la consistencia.10 Sin embargo, el
efecto sobre la probabilidad de ser
consistente, en términos marginales 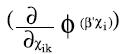 es relativamente pequeño
ya que el impacto de la edad sobre
la probabilidad marginal de ser consistente
es del 8.5% y el semestre disminuye
la probabilidad de ser consistente
en aproximadamente un 5.9%
(- 0.059).
es relativamente pequeño
ya que el impacto de la edad sobre
la probabilidad marginal de ser consistente
es del 8.5% y el semestre disminuye
la probabilidad de ser consistente
en aproximadamente un 5.9%
(- 0.059).
A continuación se explorará si las
"anomalías" encontradas se deben a
efectos de aprendizaje relacionados
con la edad o el semestre. Una forma
de explorar lo anterior consiste en que
si los individuos aprenden con la edad
a ser más consistentes, entonces a
mayor edad menor debe ser la varianza,
por la cual debería presentarse
Heterocedasticidad. Por otro lado, si
a medida que los individuos tienen
más educación (mayor semestre) son
más consistentes en sus preferencias,
también debería presentarse Heterocedasticidad.
Para conocer si estos
efectos se presentan, vamos a suponer
que los errores no son normales
y que la varianza de los mismos viene
definida como
Var[εi] = Xγ . De esta forma, una prueba
de Homoscedasticidad podría definirse
según Greene(1999 a,1999b)
como:
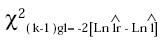
Donde X será la edad o el semestre.
Los resultados encontrados fueron:
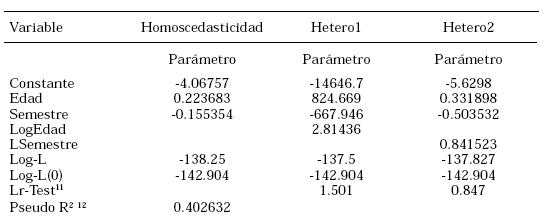
11. Lr Heter1 = -2[-138.2505-(-137.5)] = -2[-138.2505+ 137.5] = 1.501
Lr Heter2 = -2[-138.2505-(-137.827)] = -2[-138.2505+137.827] = 0.847
12. Elaborado con base en el trabajo de Zavoina y McKelvey(1975): Sea 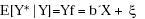 entonces R2 = [Var(Yf) / (1+var(Yf)] donde ζ es la inversa de la razón de Mill.
entonces R2 = [Var(Yf) / (1+var(Yf)] donde ζ es la inversa de la razón de Mill.
Dado que la X2(2) gl (95%) es igual a 5.99
y la X2
(2)gl(99%) es igual a 9.21, no existe
suficiente evidencia estadística
para rechazar Ho, razón por la cual,
se concluye que los errores son Homoscedásticos.
6. CONCLUSIONES
Los resultados aquí encontrados
muestran que las características socioeconómicas
como el sexo, la edad,
el ingreso, el estrato socioeconómico
y el semestre, en forma conjunta no
ayudan a explicar la consistencia en
las preferencias, lo cual implica que
no existen diferencias entre individuos,
en términos de la consistencia,
cuando estos eligen loterías.
Un hecho curioso a resaltar, consiste
en el patrón o la estructura en la consistencia
en las preferencias, ya que
usando la metodología de componentes
principales (ver Gráfica 2) existe
un patrón que agrupa la edad y el
semestre en un componente y existe
otro componente que agrupa al ingreso,
el estrato y el sexo. Las regresiones
entre la consistencia, el semestre
y la edad dieron resultados satisfactorios
(t y Lr) mientras que entre
la consistencia, el estrato, el sexo y el
ingreso no lo fueron.
Por último, la significancia estadística
de la edad no refleja efectos de
aprendizaje, pues si a mayor edad se
es más consistente, la varianza debería
disminuir con la edad y se presentaría
Heterocedasticidad; Sinembargo
esto no se encontró. La significancia
estadística encontrada,
puede significar que a mayor edad los
individuos responden con más cuidado
el cuestionario o colocan más atención
a las preguntas.
En cuanto al semestre, igual resultado
se puede derivar. La significancia
estadística no implica que a mayor
educación (mayor semestre) los individuos
aprenden a ser menos consistentes,
ya que la varianza debería
cambiar (a mayor semestre menor
varianza) y ésta se mantuvo constante.
No es claro porqué resultó significativo
el semestre (y con signo negativo).
Tal vez, la modificación en el
programa (cambios en el orden de las
asignaturas e inclusión (exclusión) de
algunas) podría generar tal resultado.
Sin embargo, esto no se comprobó
estadísticamente, razón por la cual
queda a manera de hipótesis.
NOTAS AL PIE DE PÁGINA
2. Es decir, la elección se realiza siguiendo la TUES a diferencia de otros trabajos donde la elección es estocástica.
3. Formalmente, sean los conjuntos 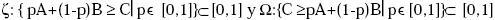 Si
ζ y Ω son cerrados se cumple la propiedad de continuidad. Un mayor refinamiento, se puede encontrar en
http://www.icesi.edu.co/~jjmora/uesp.pdf
Si
ζ y Ω son cerrados se cumple la propiedad de continuidad. Un mayor refinamiento, se puede encontrar en
http://www.icesi.edu.co/~jjmora/uesp.pdf
4. Si A 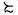 B entonces cualquier combinación de A con probabilidad p debe ser preferida a la combinación B
con probabilidad p.
B entonces cualquier combinación de A con probabilidad p debe ser preferida a la combinación B
con probabilidad p.
5. La crítica de ALLAIS a la TUES consiste en que una vez se pregunta a los individuos en torno a sus elecciones,
la mayoría prefiere A a B y D a C (Hey (1996) señala que no es muy común que se presente el patrón
B  A y C
A y C  D). El primero que repitió la prueba de ALLAIS fue MacCrimmon (1965) [Ver también MacCrimon
y Larson (1979)] quien encontró alrededor de un 40% de violaciones a la TUES. Por su parte Morrison
(1967) encontró cerca de un 30% de violación de la TUES. Slovic y Tversky (1974) encuentran un 60% de
violación de la TUES y Mascolell, Whinston y Green(1995) reportan que hicieron la prueba y encontraron
resultados consistentes con la paradoja de ALLAIS. Mora(2000) llevó a cabo la prueba en la Universidad del
Valle, durante el período enero - junio de 2000, cuyos resultados mostraron que de un total de 163 estudiantes
que respondieron a la prueba el 77.91% fueron consistentes en sus preferencias, mientras el
22.09% fueron inconsistentes con la TUES (Sobre la paradoja y otros experimentos conducidos en economía,
Hey (1996) brinda un buen material de consulta. En Montenegro(1995), también hay una buena
introducción al tema (consultar el capítulo 11)).
D). El primero que repitió la prueba de ALLAIS fue MacCrimmon (1965) [Ver también MacCrimon
y Larson (1979)] quien encontró alrededor de un 40% de violaciones a la TUES. Por su parte Morrison
(1967) encontró cerca de un 30% de violación de la TUES. Slovic y Tversky (1974) encuentran un 60% de
violación de la TUES y Mascolell, Whinston y Green(1995) reportan que hicieron la prueba y encontraron
resultados consistentes con la paradoja de ALLAIS. Mora(2000) llevó a cabo la prueba en la Universidad del
Valle, durante el período enero - junio de 2000, cuyos resultados mostraron que de un total de 163 estudiantes
que respondieron a la prueba el 77.91% fueron consistentes en sus preferencias, mientras el
22.09% fueron inconsistentes con la TUES (Sobre la paradoja y otros experimentos conducidos en economía,
Hey (1996) brinda un buen material de consulta. En Montenegro(1995), también hay una buena
introducción al tema (consultar el capítulo 11)).
6. Loomes y Sugden (1995) realizan pruebas sobre la TUES adicionando el término de error y llegan a la
conclusión de que el modelo es rechazado por los datos. Es decir, que la TUES es inadecuada como núcleo
teórico para comprobar la consistencia. Como bien mencionan Loomes, Moffatt y Sugden (1998) los datos
agregados de Loomes y Sugden(1995) no permiten sacar conclusiones con parámetros específicos a los
individuos.
7. Esta definición sigue el modelo de Fechner(1860/1966) desarrollado por Becker, DeGroot y Marschak
(1963) ya que el error en la elección se modela al adicionar un término estocástico en Cηω, el cual viene
distribuido simétricamente alrededor de cero. De esta forma, "las verdaderas preferencias" son representadas
por la TUES, pero los cálculos de valores subjetivos son sujetos a error. El modelo de Fechner es
robusto siguiendo los resultados de Ballinger y Wilcox (1997).
8. La prueba consistió en una serie de elecciones iterativas como las presentadas en el numeral 3, de las
cuales se extrajeron tres pares de elecciones aleatoriamente.
9. Para comprobar la hipótesis Ho: β1=β2=β3=β4=β5=0 (se excluye la constante β0 ), se usó Lr - test, el cual
sigue una X2(k-1) gl . De esta forma, 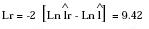
10. Por otro lado, las correlaciones entre la edad y el semestre no muestran un claro patrón de comportamiento.
Esto además excluye la posibilidad de que exista multicolinealidad en los datos:

7. BIBLIOGRAFIA
BALLINGER, T.P and N.T Wilcox.
(1997). Decision, error and heterogeneity.
Economic Journal,
107, 1090-1105.
BARTHOLOMEW, D.J. (1984). The foundations
of factor analysis. Biometrika,
71, 221-232.
BECKER, G.M, M.H DeGroot, and J.
MARSCHAK. (1963). Stochastic
models of choice behavior. Behavioral
Science, 8, 41-55.
CATTEL, R.B. (1966). The scree test for
the number of factors. Multivariate
Behavioral Research,
1, 245-276.
FECHNER, G. (1860 / 1966). Elements
of Psychophysics. Vol. 1, New
York: Holt Rinehart and Winston.
GREENE, W.H. (1999a). Limdep, versión
7.0(1985-1999). Econometric
Software, Inc.
GREENE, W.H. (1999b). Análisis
Econométrico. Tercera edición,
Iberia: Prentice Hall.
HARLES, D and C.F. Camerer. (1994).
The predictive utility of generalized
expected utility theories.
Econométrica, 62, 1251-1289.
HEY, J.D. (1995). Experimental investigations
of errors in decision
making under risk. European
Economic Review, 39, 633-640.
HEY, J.D. (1996). Experimentos en
economía. México: Fondo de Cultura de
México.
HEY, J.D. and C.D, ORME. (1994). Investigating
generalizations of expected
utility theory using experimental
data. Econométrica,
62, 1291-1326.
KAISE, H.F. (1960). The application
of electronic computers to factor
analysis. Educational and
Psychological Measurement,
20, 141-151.
LOOMES, G. y SUGDEN, R. (1995). Incorporation
a stochastic element
into decision theories.
European Economic Review,
39, 641-648.
LOOMES, G., P.G MOFFATT and R. SUGDEN.
(1998). A Microeconometric
test of alternative stochastic
theories of risky choice. The
Economics Research Center,
Discussion paper No. 9806,
School of Economics and Social
Studies, University of East
Anglia.
MACCRIMMON, K.R. (1965). An experimental
study of the decision
making behavior of business
executives. Tesis doctoral no
publicada, Universidad de California,
Los Ángeles.
MACCRIMMON, K.R. and S. LARSON. (1979). Utility theory:
Axioms versus paradoxes.
en M. Allais y O. Hagen, The expected utility hypothesis
and the ALLAIS paradox. Autor: Dordrecht, Holland. pp. 333-409.
MAS-COLELL, A., WHINSTON, M.D y
GREEN, J.R. (1995). Microeconomic
Theory. New York: Oxford University
Press.
MONTENEGRO, A.G. (1995). Introducción
a la economía experimental. Bogotá:
Ediciones Uniandes, Ecoe.
MORA, J.J. (2000). La Paradoja de
ALLAIS y la Teoría de la Utilidad
Esperada: ¿Qué tan consistentes
son en sus preferencias
los estudiantes de
Economía de la Universidad
del Valle? Grupo de teoría
económica, Universidad del
Valle. Junio. En http://www.icesi.edu.co/~jjmora/Allais.pdf
MORRISON, D.G. (1967). On the consistency
of preferences in Allais´ paradox. Behavioral Science 12, 373-383.
STARMER, C. (2000). Developments in
non-expected utility theory: The
hunt for a descriptive theory of
choice under risk. Journal of
Economic Literature, Vol. 38,
jun, 332-382.
SLOVIC, P y TVERSKY, A. (1974). Who
accepts Savage´s axiom?, Behavioral
Science, 19, 368-73.
ZAVOINA, R. and MCELVEY, W. (1975).
A statistical model for the analysis
of ordinal level dependent
variables. Journal of Mathematical
Sociology, summer,
103-120
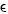 [0,1]. Una
serie de resultados específicos serán
loterías degeneradas con probabilidad
de uno. Denótese la relación "A
es al menos tan buena como
B" a A
[0,1]. Una
serie de resultados específicos serán
loterías degeneradas con probabilidad
de uno. Denótese la relación "A
es al menos tan buena como
B" a A 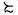 B, la relación "A preferido a
B" como A
B, la relación "A preferido a
B" como A  B y la relación "A indiferente
a B" como A
B y la relación "A indiferente
a B" como A  B. Los siguientes
axiomas sobre las preferencias deben
cumplirse:
B. Los siguientes
axiomas sobre las preferencias deben
cumplirse: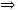 A
A 
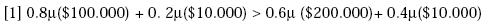
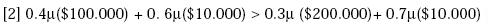
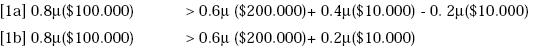
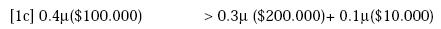
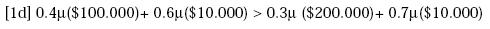
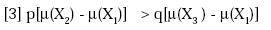
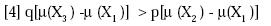
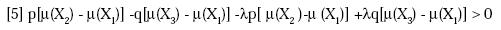
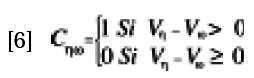
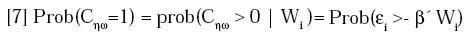
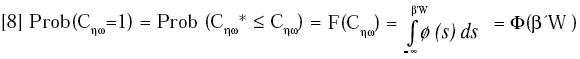




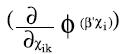 es relativamente pequeño
ya que el impacto de la edad sobre
la probabilidad marginal de ser consistente
es del 8.5% y el semestre disminuye
la probabilidad de ser consistente
en aproximadamente un 5.9%
(- 0.059).
es relativamente pequeño
ya que el impacto de la edad sobre
la probabilidad marginal de ser consistente
es del 8.5% y el semestre disminuye
la probabilidad de ser consistente
en aproximadamente un 5.9%
(- 0.059).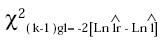

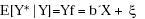 entonces R2 = [Var(Yf) / (1+var(Yf)] donde ζ es la inversa de la razón de Mill.
entonces R2 = [Var(Yf) / (1+var(Yf)] donde ζ es la inversa de la razón de Mill.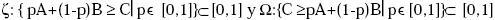 Si
ζ y Ω son cerrados se cumple la propiedad de continuidad. Un mayor refinamiento, se puede encontrar en
Si
ζ y Ω son cerrados se cumple la propiedad de continuidad. Un mayor refinamiento, se puede encontrar en