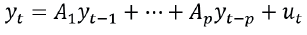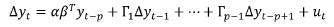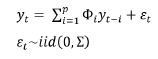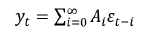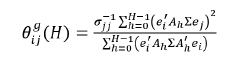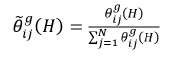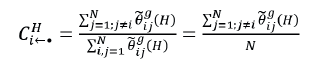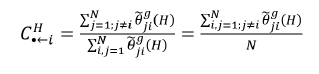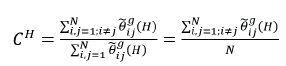1. Introducción
La globalización financiera ha promovido la libre movilidad de capitales desde y hacia el exterior (Bekaert y Harvey, 1999), lo que ha fomentado la creación de bloques de integración financiera o económica. En la Gran Bretaña del siglo XVIII o en Alemania e Italia en el XIX, ya se percibían antecedentes de integración, pero es hasta después de la Segunda Guerra Mundial que este proceso involucra a varias economías; por ejemplo, la Comunidad Económica Europea (CEE), el Mercado Común de Centroamérica (MCCA), el Tratado entre México, Estados Unidos y Canadá (T-MEC)1, los acuerdos del Sudeste Asiático (ASEAN) y el Mercado Común del Cono Sur (MERCOSUR) (Corral, 2011). A comienzos el siglo XXI, surge el Mercado Integrado Latinoamericano (MILA), contraparte financiera de la iniciativa de integración económica denominada Alianza del Pacífico (AP), que pretende incrementar el crecimiento, desarrollo y competitividad de las economías del litoral asiático del Pacífico. El MILA busca ser un mercado bursátil eficiente, amplio y variado, y pone a disposición de emisores e inversionistas más y mejores oportunidades de captación y asignación de recursos en mercados del Cono Sur: Chile, Colombia, México y Perú (Martínez, Narváez y Echeverry, 2012; Campos y Revoredo, 2017)2.
El MILA inicia operaciones con 546 empresas listadas (84 colombianas, 235 peruanas y 227 chilenas), para septiembre de 2020 alcanza las 619 emisoras, de las cuales 67, 214, 198 y 140 corresponden a los mercados de Colombia, Perú, Chile y México, respectivamente.
Espinosa, Gorigoitía y Vieito (2017) destacan que el MILA se caracteriza porque cada mercado ha mantenido su independencia y autonomía regulatoria; sin embargo, detonó la aparición de estrategias de integración horizontal en empresas del sector financiero, como el caso de Credicorp, grupo financiero peruano que adquirió Correval, agente importante de la Bolsa de Colombia3. Otro ejemplo es el del banco chileno CorpBanca, que en 2012 compró el Banco Santander Colombia y en 2013 el Helm Bank (Vargas y Bayardo, 2013).
La tabla 1 muestra aspectos importantes en la evolución del MILA. La cantidad de emisoras ha sido estable con variaciones del 1% para los casos de Colombia y Perú. El volumen operado en el mercado bursátil mexicano lidera a sus contrapartes, seguido de Chile, Colombia y Perú. La capitalización bursátil mantiene un comportamiento similar al volumen, aunque llama la atención la evolución a finales del 2020, cuando ya se perciben los efectos económicos ocasionados por la pandemia de la COVID-19 y el entorno recesivo mundial que ya aquejaba la economía mundial. Perú sufrió la menor caída (16%), aunque ese mercado apenas abarca el 2% del volumen operado en la región; Chile, México y Colombia mostraron desplomes del orden del 33, 36 y 42%, respectivamente, es decir, los mercados que representan el 98% del volumen sufrieron una caída promedio del 37% en el nivel de capitalización bursátil.
Tabla 1 Evolución reciente de cifras relevantes del MILA
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
|---|---|---|---|---|---|---|---|
| Chile | Volumen * | 1,28 | 2,38 | 4,16 | 6,73 | 5,10 | 2,12 |
| Capitalización * | 401 | 210 | 296 | 250 | 206 | 153 | |
| Emisoras | 224 | 217 | 212 | 205 | 203 | 198 | |
| Colombia | Volumen * | 0,81 | 1,27 | 1,18 | 0,72 | 0,86 | 0,68 |
| Capitalización * | 88 | 104 | 122 | 105 | 133 | 81 | |
| Emisoras | 73 | 71 | 69 | 68 | 68 | 67 | |
| México | Volumen * | 10,90 | 9,71 | 8,97 | 7,17 | 6,94 | 7,5 |
| Capitalización * | 91 | 352 | 416 | 385 | 415 | 311 | |
| Emisoras | 276 | 137 | 141 | 140 | 139 | 140 | |
| Perú | Volumen * | 0,09 | 0,19 | 0,35 | 0,32 | 0,20 | 0,18 |
| Capitalización * | 191 | 124 | 99 | 93 | 104 | 88 | |
| Emisoras | 173 | 280 | 134 | 225 | 214 | 214 |
* Cifras en miles de millones de dólares al mes de diciembre, excepto en 2020, año en que el último reporte en la página de MILA es de septiembre.
Fuente: elaboración propia con base en la información del sitio oficial de MILA http://mercadomila.com
El presente estudio contribuye a la literatura en dos aspectos. En primer lugar, se analiza la evolución de las relaciones entre los mercados de capital en la región MILA, a la luz de la influencia que ejerce el mercado bursátil de Estados Unidos. En segundo lugar, la investigación complementa los hallazgos de literatura previa que analiza la integración financiera al proponer otra alternativa para analizar esas relaciones. Con base en la metodología propuesta por Diebold y Yilmaz (2009a, 2009b, 2012), este estudio tuvo por objetivo construir índices de derrames (spillovers) para analizar la forma en que se propagan los choques entre los rendimientos diarios del S&P500 y los índices bursátiles de los países del MILA, entre el 30 de octubre del 2009 y el 23 de abril del 2020. El análisis comprueba la existencia de relaciones significativas y se verifica la importancia del mercado accionario de Estados Unidos en los mercados del MILA. Como se esperaba, desde inicios del 2020, el nivel de conectividad entre todos los mercados creció y la influencia del S&P500 ascendió, aunque durante el periodo analizado no alcanzó la influencia que mostró en años previos.
En la siguiente sección se discute la literatura relevante, luego se enuncia la metodología propuesta por Diebold y Yilmaz (2009a, 2009b, 2012), que se basa en la estimación de modelos de vectores autorregresivos (VAR) mediante una ventana móvil de ancho fijo, la cual se extiende en este artículo para capturar los derrames ocurridos desde y hacia el mercado accionario estadounidense y los mercados del MILA durante el horizonte temporal cubierto por este estudio. Los resultados del análisis de los datos correspondientes a dichos mercados se muestran en la cuarta sección. Finalmente, se presentan las conclusiones.
2. Marco teórico
2.1 Integración financiera internacional
Dado que, como lo señalan el Fondo Monetario Internacional (2016) y Eyraud, Singh y Sutton (2017), la integración financiera es el proceso por el cual los mercados financieros de dos o más países o regiones se vuelven más conectados entre sí, ante el fortalecimiento de los vínculos financieros entre los mercados, ocasionado por la creciente integración, se ha observado, en el corto plazo, la transmisión de perturbaciones entre ellos, así como tendencias comunes en el largo plazo (Kasa, 1992). Dicha integración promueve beneficios como el incremento de opciones de financiamiento, del valor de la empresa, de las posibilidades de diversificación y la reducción del costo de capital (Mellado y Escobari, 2015; Sandoval et al., 2015; Campos y Revoredo, 2017). Por otro lado, también existen efectos no deseados sobre el precio de los activos y el consecuente interés de formar portafolios que diversifiquen los riesgos sistemáticos domésticos (Chambet y Gibson, 2008; Romero, Ramírez y Guzmán, 2013).
Entre los esfuerzos pioneros que discuten la propagación de efectos a través de los mercados, en el ámbito de las crisis que se gestaron desde la década del noventa, figuran Calvo y Reinhart (1996) 4, Rigobón (2002), Forbes y Rigobon (2002), Bekaert y Harvey (2003) y Bekaert, Harvey y Ng (2005). La crisis de mercados emergentes de los noventa, la crisis hipotecaria del mercado de Estados Unidos del 2007 y la crisis de deuda europea del 2010 son ejemplos recientes de descalabros financieros relevantes, en función del impacto negativo de tales choques en los mercados internacionales (Santillán, Gurrola y López, 2017).
La transmisión de efectos financieros desde el mercado bursátil de Estados Unidos a causa de la crisis subprime ha sido ampliamente estudiada; por ejemplo, Mohti, Dionísio, Vieira y Ferreira (2019) encontraron evidencia de esos efectos en 18 mercados bursátiles en países de América Latina, Europa, África, Oriente Medio y Asia. Mediante un modelo VARMA-GARCH-DCC, López, Ortiz y Cabello (2009) ofrecen evidencia de integración en los mercados accionarios de la región del Tratado de Libre Comercio de América del Norte (TLCAN). Mediante la metodología wavelet, Dima, Dima y Barna (2015) encontraron integración y procesos de sincronización de corto y mediano plazo en los mercados de México, Brasil y Chile.
Es importante medir la conectividad (o conjunto de conexiones) que surge de la integración entre los mercados financieros, entre otras razones, por el riesgo de las inversiones, ya que surge de (y contribuye a) la vinculación entre las fuentes y usos de los recursos disponibles en los mercados financieros, y canaliza ahorros a inversiones reales cuyos efectos impactan a la economía e integran los mercados financieros en los niveles regional y mundial (Diebold y Yilmaz, 2015a)5.
2.2 Relaciones entre los mercados del MILA
La integración financiera en el MILA es de interés académico, entre otras explicaciones, porque un mercado bursátil sólido promueve el desarrollo comercial -a través de mayores alternativas de inversión y financiamiento-, ofrece una mayor presencia y visibilidad de las emisoras (Sandoval et al. 2015) y mejora las perspectivas de inversión extranjera (Bolaños, Burneo, Galindo y Berggrun 2015; Orozco-Álvarez y Ramírez-López, 2016). Otras razones son la reducción de costos de transacción (Sandoval y Soto, 2016), el incremento de las correlaciones en los rendimientos accionarios (Espinosa et al., 2017; Santillán, Massa y Reyna, 2017), las posibilidades de arbitraje (García y Rosso, 2016; Gil, 2020), los altos niveles de volatilidad y desajustes financieros, entre otros aspectos (Martínez et al. 2012; Vargas y Bayardo, 2013).
La evidencia sobre las relaciones entre los mercados del MILA incluye estudios de casos, que aseguran que el proceso de integración ha propiciado modificaciones en la intermediación financiera (corretaje) en el mercado de Colombia (Yepes, Gonzales y González, 2015). Mediante el análisis gráfico de tendencias, Bolaños et al. (2015) concluyen que el volumen presenta un balance negativo, así como un efecto marginal en la rentabilidad. Gil (2020), al utilizar simulación de operaciones bursátiles, sugiere un limitado avance de la integración caracterizado por asimetrías importantes en rentabilidad, capitalización, nivel de concentración, ente otros aspectos. Mediante la técnica de mínimos cuadrados ordinarios (MCO), García y Rosso (2016) sugieren posibilidades de arbitraje al demostrar efectos estacionales (calendario). Fuenzalida, Berggrun y Mongrut (2017), con el modelo de tres factores de Fama y French, encontraron una relación positiva entre la prima de liquidez y los rendimientos accionarios. Uribe y Mosquera (2014), a partir de la razón de Sharpe, rechazan rompimientos estructurales en el proceso generador de datos asociado a la eficiencia de los portafolios.
La mayor parte de la evidencia empírica sobre integración financiera en el MILA gira en torno a las relaciones de largo plazo y el cambio en las correlaciones de los rendimientos. Tales estudios confirman relaciones de equilibrio de largo plazo (Sandoval y Soto, 2016); aumento en las correlaciones lineales y reducción en las dependencias no lineales; es decir, la integración financiera no reduce las posibilidades de diversificación de largo plazo (Santillán et al., 2017). Otros resultados sostienen que el incremento de las relaciones de dependencia atiende al aumento del volumen negociado en el mercado menos desarrollado: la Bolsa de Lima. Si bien el acuerdo genera beneficios de diversificación a todos los miembros, estos se mantienen solo en el corto plazo y disminuyen a medida que se incrementa el nivel de integración (Espinosa et al., 2017). Cardona, Gutiérrez y Agudelo (2017) y Rodríguez y Perrotini (2019) documentaron transmisiones de volatilidad y relaciones de contagio entre los mercados de la región MILA, incluyendo en su análisis además a Brasil, Argentina y el mercado de Estados Unidos. Recientemente, Muñoz, Sepúlveda, Velosos y Delgado (2020) aseguraron que el acuerdo no ha generado cambios importantes en la integración de la región, aunque la adhesión de México contribuyó a disminuir la volatilidad entre los rendimientos.
Otros estudios abordan los mercados del MILA al analizar los valores extremos en las distribuciones de los rendimientos a partir de la metodología de cópulas. Loaiza, Gomez y Melo (2015) incluyeron en su análisis a Brasil y a Argentina y encontraron que los rendimientos accionarios de la región mantienen relaciones asimétricas de dependencia significativa (contagio) en los valores de la cola inferior. Por otro lado, Sosa, Ortiz y Cabello (2018) comprobaron que los rendimientos evolucionan en atención a dos regímenes distintos: baja y alta volatilidad; este último presenta menos persistencia que el primero.
2.3 COVID-19 y los mercados financieros
Evidencia empírica reciente ha demostrado algunos efectos que el coronavirus SARS-CoV-2 ha tenido sobre los mercados financieros internacionales; por ejemplo, que el crecimiento diario de casos confirmados y el total de fallecimientos por la COVID-19 tienen efectos negativos en la rentabilidad de los mercados bursátiles (Al-Awadhi, Alsaifi, Al-Awadhi y Alhammadi, 2020); también se confirma la presencia de conexiones entre la propagación de la COVID-19 y los mercados financieros globales (Ali, Alam y Rizvi, 2020).
3. Metodología
Diebold y Yilmaz (2009a) proponen un método para capturar la dinámica en el tiempo de la conectividad a partir de los spillovers (derrames) que ocurren como consecuencia de los choques de los miembros de los sistemas formados por dos o más mercados. Diebold y Yilmaz (2009b) argumentan que ese método es mejor que el de Edwards y Susmel (2001), ya que no se basa en una variable dicotómica de estado con valores 0 y 1, sino que permite variación continua en los números reales. Los índices de spillovers propuestos por Diebold y Yilmaz (2009a) proveen una medición de la contribución neta de un mercado en el mecanismo de transmisión de información de otro mercado, por lo que son un instrumento adecuado para capturar la dinámica de la conectividad.
Un modelo VAR se puede representar como
Si el sistema es cointegrado, se puede especificar como el mecanismo de corrección de errores, denominado modelo vectorial de corrección del error (VECM).
Este modelo captura las relaciones de corto y de largo plazo.
Además, un sistema de N variables que pueda especificarse como un VAR(p) estacionario en covarianza de la forma
acepta la representación del proceso como
Esta representación permite estudiar los efectos de los choques en las variables del sistema cuyos integrantes están conectados mediante vínculos económicos (Diebold y Yilmaz, 2015b) o, para efectos de este estudio, vínculos financieros, como en Diebold y Yilmaz (2009, 2012), quienes construyeron un índice para el análisis de derrames entre las variables del VAR. Diebold y Yilmaz (2014) mostraron la utilidad de su metodología para el análisis y medición de la conectividad en las redes financieras. La contribución que hace la variable j a la varianza del error general del pronóstico de la variable i para los H periodos (pasos) posteriores, H=1,2,..., puede medirse por
Σ es la matriz de varianzas-covarianzas del vector εt que contiene los términos de perturbación del VAR; σjj es la desviación estándar de la perturbación de la j-ésima ecuación, y ei es el vector seleccionado con valor unitario en el i-ésimo elemento y cero en los demás. En otras palabras, la descomposición de la varianza, análisis típico de los modelos VAR, indica la cantidad de información con la que cada variable contribuye a las demás variables del sistema analizado.
La dimensión del sistema hace posible que surjan problemas para identificar los choques, lo que comúnmente se aborda utilizando la factorización ortogonal de Cholesky para considerar la correlación entre esos choques. Dicha factorización es sensible al ordenamiento de las variables, por lo que para superar el problema de identificación Diebold y Yilmaz (2012), con base en Koop, Pesaran y Potter (1996) y Pesaran y Shin (1998), se propone la normalización
que proporciona el spillover/conectividad direccional en parejas, base de las medidas del spillover/conectividad total direccional. La correspondiente al spillover/ conectividad con dirección hacia la variable i desde las demás variables j se define como
y el spillover/conectividad total con dirección desde la variable i hacia las demás variables j como,
El spillover/conectividad de todo el sistema está dado por
Con base en una ventana temporal corrediza, se pueden analizar los spillovers/conectividad en el tiempo.
4. Análisis de los resultados
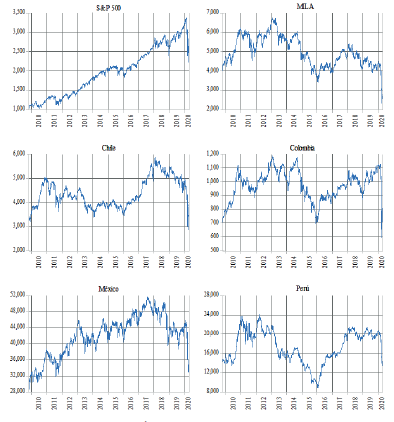
La figura 1 muestra la evolución del S&P500 y de los índices del MILA como bloque, y de los mercados individuales: Chile, Colombia, México y Perú, del 30 de octubre del 2009 al 23 de abril del 20206. Las 2708 observaciones de esos índices cubren el periodo previo a la fuerte caída observada el 23 de marzo de 2020 en los mercados financieros de todo el mundo y un mes después; es decir, permite capturar el historial previo a la caída y el regreso del S&P500 a los niveles en que se encontraba dos años antes, cuando nadie podía anticipar que, en 2020, además de tensiones por la guerra de precios del petróleo, en un contexto mundial recesivo, se enfrentaría una contingencia sanitaria de la magnitud de la pandemia de la COVID-19. Ante la crisis económica generada por la irrupción de la pandemia, el Gobierno de Estados Unidos y la Reserva Federal implementaron diferentes medidas de apoyo económico a los particulares, así como a empresas productivas y financieras, lo que permitió que se superase muy rápidamente la crisis en los mercados financieros de ese país y, de manera particular, el bursátil, que después de la fecha de la mencionada caída no ha detenido su tendencia al alza hasta el momento en que se escribieron estas líneas. Para poder comparar los datos, se eliminaron todas las observaciones de los días en los cuales al menos uno de los mercados no operó.
Como se puede apreciar en la figura 1, los mercados de Chile, Colombia y Perú tienen una evolución más o menos similar a la del MILA, con excepción de México; quizá porque este país se incorporó al acuerdo hasta el 2014, su evolución es más próxima a la del S&P500, con el que se espera que esté más integrado, tanto por la vecindad geográfica entre los dos países como por las más de dos décadas del proceso de integración económico-financiera. No obstante, se observa que el crecimiento del mercado estadunidense en la mayor parte del periodo parece más estable y sostenido que el del mercado mexicano. Los mercados de México, de Chile y del MILA muestran una tendencia claramente decreciente desde finales del 2017 que se prolonga hasta principios del 2020. Sin embargo, en lo que sí coinciden todos los mercados bajo consideración es en la notable caída que han mostrado desde principios del 2020 y hasta el periodo estudiado.
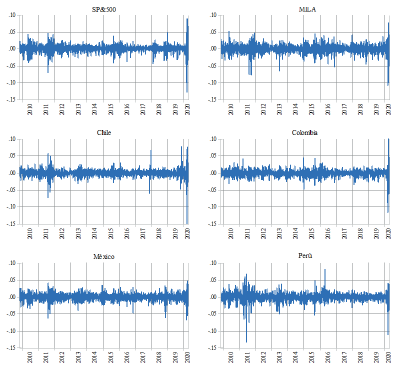
En la tabla 2 se muestran las estadísticas básicas de los rendimientos de los mercados analizados, y en la figura 2 se muestra su evolución. En esta figura (figura 2) se pueden apreciar clusters de volatilidad en determinados periodos de tiempo, característicos de las series de tiempo financieras. Los rendimientos de los mercados del MILA, de México y de Perú muestran una mayor volatilidad en comparación con los del S&P500, Chile y Colombia. No obstante, la mayoría de los mercados registran una mayor volatilidad desde principios del 2020, con excepción de Perú; sin embargo, la variabilidad de los rendimientos en este mercado sugiere que se presentó un periodo de gran volatilidad en 2011.
Tabla 2 Estadísticas básicas de los rendimientos S&P500 y MILA
| SP&500 | MILA | Chile | Colombia | México | Perú | |
|---|---|---|---|---|---|---|
| Media | 0,0367% | -0,0154% | 0,0046% | 0,0028% | 0,0066% | 0,0004% |
| Mediana | 0,0574% | 0,0265% | 0,0120% | 0,0287% | 0,0226% | 0,0333% |
| Máximo | 8,9683% | 7,7379% | 7,7586% | 12,9198% | 4,7439% | 8,2616% |
| Mínimo | -12,7652% | -10,7441% | -15,2155% | -11,7344% | -6,6381% | -13,2908% |
| Desviación estándar | 1,0750% | 1,1906% | 0,9933% | 1,0065% | 0,9334% | 1,1252% |
Fuente: elaboración propia.
En la tabla 3 se observa que, en comparación con lo ocurrido hasta 2019, las correlaciones de los rendimientos del S&P500 y los mercados del MILA cambiaron durante la parte de 2020 cubierta por este estudio. La correlación del índice del MILA con el S&P500 se redujo a menos de la mitad del valor previo, contrario a lo que se sabe en relación con los incrementos de correlación durante periodos críticos. No obstante, cuando se consideran los mercados individuales, sus correlaciones crecieron con el S&P500, pero disminuyeron respecto del MILA. Se observan fuertes incrementos de las correlaciones entre los mercados integrantes del MILA. Es conveniente considerar que la correlación es solo una medida para capturar la fuerza de la asociación lineal existente entre los rendimientos, razón por la que sus alcances son limitados para efectos del análisis presentado en este artículo.
Tabla 3 Correlaciones de los rendimientos S&P500 y MILA
| SP&500 | MILA | Chile | Colombia | México | Perú | |
|---|---|---|---|---|---|---|
| SP&500 | 1 | 0,3040 | 0,6402 | 0,5558 | 0,7729 | 0,7551 |
| MILA | 0,6225 | 1 | 0,2760 | 0,2522 | 0,0043 | 0,0924 |
| Chile | 0,4276 | 0,6680 | 1 | 0,6896 | 0,5070 | 0,6639 |
| Colombia | 0,3836 | 0,5254 | 0,3819 | 1 | 0,4856 | 0,5820 |
| México | 0,5956 | 0,7894 | 0,4645 | 0,3663 | 1 | 0,7625 |
| Perú | 0,4266 | 0,5162 | 0,3684 | 0,3011 | 0,3698 | 1 |
Debajo de la diagonal principal se muestran las correlaciones del inicio de las observaciones a 2019, las que están arriba corresponden a la parte de 2020 que se analiza.
Fuente: elaboración propia.
Kasa (1992) demostró que la cointegración es evidencia formal de integración en los mercados financieros, pues se supone que los mercados del MILA están integrados entre sí y con el mercado accionario estadunidense, por lo que, antes de aplicar el método de Diebold y Yilmaz para el análisis de derrames/conectividad, es pertinente considerar que el modelado VAR debe tomar en cuenta la(s) relación(es) de largo plazo que se espera observar en un bloque de mercados integrados. Las pruebas de raíz unitaria Dickey-Fuller aumentada aplicadas al logaritmo natural de los índices accionarios de los mercados analizados se muestran en la tabla 4. El resultado de dichas pruebas, bajo diferentes especificaciones, sugiere que todos los índices bajo estudio poseen una raíz unitaria en virtud de que los resultados de la aplicación de dicha prueba a los rendimientos, obtenidos como la primera diferencia de las series en forma logarítmica, resultaron ser estacionarios, es decir, son I (0).
Tabla 4 Pruebas de Raíz Unitaria Dickey-Fuller Aumentada
| SCoT | C | CyT | |
|---|---|---|---|
| ADF t | ADF t | ADF t | |
| Logaritmos | |||
| S&P500 | 2,1786 | -1,25053 | -3,0800 |
| MILA | -0,6977 | -0,6979 | -2,0873 |
| Chile | 0,2523 | -2,5874 * | -2,1245 |
| Colombia | -0,0030 | -2,8709 ** | -2,7934 |
| México | 0,2173 | -2,2970 | -1,2385 |
| Perú | -0,0147 | -1,9442 | -1,9367 |
| Log-rendimientos | |||
| S&P500 | -12,6005 *** | -12,6011 *** | -12,6955 *** |
| MILA | -12,8493 *** | -12,8469 *** | -12,9308*** |
| Chile | -9,9620 *** | -9,9613 *** | -10,1275 *** |
| Colombia | -9,8409 *** | -9,8658 *** | -10,0437 *** |
| México | -9,6456 *** | -9,6437 *** | -9,6777 *** |
| Perú | -11,7019 *** | -11,9216 *** | -11,9438 *** |
SCoT = sin constante o tendencia, C =con constante, CyT = constante y tendencia, ADF t = estadístico t de la prueba Aumentada de Dickey- Fuller (ADF). ***, **, * denotan, respectivamente, el 1%, 5% y 10% de significancia.
Fuente: elaboración propia.
La tabla 5 muestra las pruebas de cointegración de Johansen entre los índices accionarios de los mercados analizados, efectuada con ocho rezagos en el VAR. Como se puede ver, se rechaza la hipótesis de no cointegración para el logaritmo natural de los índices accionarios del S&P500 y el MILA de acuerdo con las pruebas de la traza y del máximo valor eigen; esto sugiere que existe una relación de largo plazo entre ellos. Para el S&P500 y los mercados que conforman el MILA, únicamente la prueba de la traza rechaza la hipótesis nula de no cointegración entre esos mercados y sugiere que solo hay una relación de largo plazo.
Tabla 5 Pruebas de cointegración de Johansen
| S&P500 y MILA | ||||
| H0: | Traza | v.c. 5% | Max-eigen* | v.c. 5% |
| r=0 | 14,3975 | 12,3209 | 12,5719 | 11,2248 |
| r ≤ 1 | 1,8256 | 4,1299 | 1,8256 | 4,1299 |
| S&P500, Chile, Colombia, México y Perú | ||||
| H0: | Traza | v.c. 5% | Max-eigen* | v.c. 5% |
| r=0 | 97,2929 | 88,8038 | 44,0724 | 88,8038 |
| r ≤ 1 | 53,2205 | 63,8761 | 24,0571 | 63,8761 |
| r ≤ 2 | 29,1635 | 42,9152 | 15,6307 | 42,9152 |
| r ≤ 3 | 13,5327 | 25,8721 | 9,2104 | 25,8721 |
| r ≤ 4 | 4,3223 | 12,5180 | 4,3223 | 12,5180 |
*Prueba del máximo eigenvalor, v.c. = valor crítico.
Fuente: elaboración propia.
La tabla 6 muestra los resultados de los spillovers estimados para los rendimientos de los mercados S&P500 y del MILA, en primer lugar, y, posteriormente, entre los rendimientos del S&P500 y de cada uno de los mercados accionarios que lo conforman. En ambos paneles, la entrada ij-ésima es la contribución a la varianza del error de pronóstico proveniente de innovaciones de los rendimientos del mercado al mercado j. Cada variable (índice) está asociada con los rendimientos en uno de los mercados examinados, los elementos diagonales (=) miden los spillovers propios de los rendimientos de cada mercado, mientras que los elementos fuera de la diagonal (≠) miden los spillovers de los rendimientos cruzados entre los mercados analizados. Además, las sumas por fila que excluyen los elementos diagonales principales (de otros) y las sumas de columna (contribución a otros) muestran los spillovers de los rendimientos totales hacia (recibido por) y desde (transmitido por) cada mercado. El índice de spillovers de los rendimientos, que se muestra en la esquina inferior derecha, es aproximadamente igual a la suma de la gran columna fuera de la diagonal (o suma de la fila) en relación con la suma de la gran columna, incluidas las diagonales.
Tabla 6 Spillovers (conectividad) de los rendimientos
| S&P500 y MILA | ||||||
| S&P500 | MILA | Desde | ||||
| S&P500 | 74,76 | 25,24 | 12,62 | |||
| MILA | 25,45 | 74,55 | 12,72 | |||
| Hacia | 12,72 | 12,62 | 25,34 | |||
| S&P500 y mercados integrantes del MILA | ||||||
| SP&500 | Chile | Colombia | México | Perú | Desde | |
| SP&500 | 40,40 | 12,75 | 20,12 | 18,24 | 8,50 | 11,92 |
| Chile | 15,82 | 41,14 | 21,15 | 13,54 | 8,35 | 11,77 |
| Colombia | 14,29 | 9,18 | 55,14 | 12,50 | 8,89 | 8,97 |
| México | 17,00 | 15,12 | 16,79 | 45,83 | 5,26 | 10,83 |
| Perú | 10,53 | 20,43 | 30,72 | 10,13 | 28,19 | 14,36 |
| Hacia | 11,53 | 11,49 | 17,76 | 10,88 | 6,20 | 57,86 |
Fuente: elaboración propia.
En el primer panel de la tabla 6, se observan algunos resultados interesantes. Los efectos de contagio entre los rendimientos son mayores dentro de los mercados que entre mercados, lo cual es consistente con lo encontrado por Fowowe (2017) y Rodríguez, Muller y Climent (2021). Por lo tanto, las innovaciones en los rendimientos en el mercado de valores del S&P500 son responsables del 74,76% de la varianza del error de pronóstico de los rendimientos de las acciones del S&P500. De manera similar, las innovaciones en el mercado de valores del MILA representan el 74,55% de la variación del error de pronóstico de los rendimientos de este mercado. En lo que respecta a los spillovers entre los mercados, los resultados de la tabla 6 muestran una notable interdependencia entre los mercados de valores pertenecientes al MILA y el S&P500. Como se desprende de dicha tabla, los spillovers del S&P500 son mayores para México y Chile y los de Chile hacia los de Perú y México. No obstante, el mercado accionario que más spillovers de rendimientos propaga es el de Colombia, incluso más que el del S&P500, en tanto que el mercado que menos choques emite es el de Perú. Por otro lado, el mercado que más choques recibe es el S&P500 y el que menos choques recibe es el de Colombia.
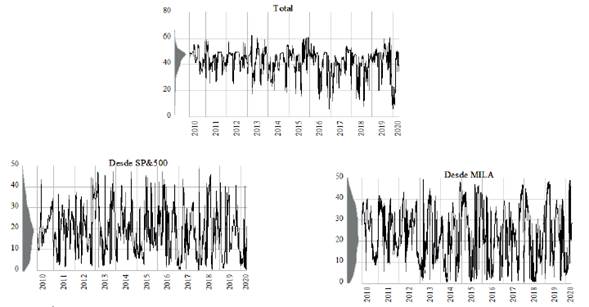
Aunque los resultados presentados en la tabla 6 brindan información útil sobre los efectos de contagio entre los mercados de interés, los valores presentados en dicha tabla son índices de contagio promedio durante el período de la muestra y estos pueden ocultar movimientos seculares o cíclicos potencialmente importantes en los efectos de contagio, o información o eventos interesantes que ocurrieron en toda la muestra (Fowowe, 2017; Rodríguez et al., 2021). Por lo tanto, no se espera que los índices promedio de la tabla 6 sean constantes a lo largo de todo el período de la muestra y, para examinar cómo evolucionan estos efectos indirectos a lo largo del tiempo, se estima el modelo utilizando ventanas móviles de 100 días, como el número de observaciones en cada paso. Se evalúa la dinámica de la variación de los spillovers examinando su magnitud a lo largo del tiempo (figura 3), para los rendimientos del S&P500 y del MILA, y en la figura 4 para el S&P500 y todos los mercados que conforman el MILA, en ambos casos se presentan tanto la evolución del spillover total como la contribución de los spillovers de cada mercado individual.
Fuente: elaboración propia.
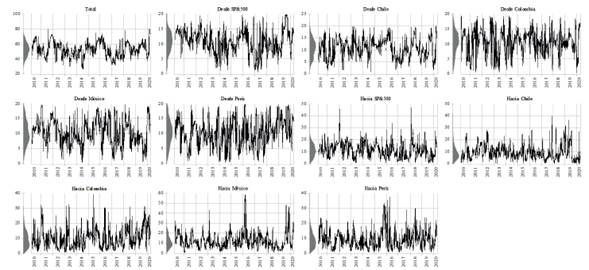
Figura 4 Spillover/conectividad total y contribuciones S&P500-Mercados MILA
La evolución de los spillovers total y desde S&P500 muestra una cierta volatilidad que se mantiene dentro de un intervalo relativamente constante, mientras que los spillovers provenientes del MILA muestran un ligero incremento en lo que va del 2020, que tiende a reducirse ligeramente para finales de la muestra analizada; lo que sugiere, de este modo, que la crisis de la COVID-19 incrementó la transmisión de choques del MILA al SP&500 y no a la inversa.
En lo que se refiere a la evolución de los spillovers totales, cuando se estiman incorporando en el modelo los mercados accionarios que pertenecen al MILA, los resultados son distintos, ya que el índice de spillovers totales se mantiene relativamente estable en la mayor parte del periodo de la muestra y tiende a incrementarse de manera notable hacia finales de la muestra, debido a la crisis de la COVID-19, lo cual se interpreta como un mayor contagio entre los mercados analizados. De igual forma, los spillovers provenientes de los mercados de México y de Chile hacia el resto de los mercados fueron los que más se incrementaron a lo largo del 2020, como consecuencia de la crisis sanitaria y económica que desató la COVID-19. En tanto que la mayoría de los mercados analizados muestran que recibieron una mayor cantidad de spillovers dentro del periodo estudiado en 2020, pero no en una mayor cuantía de la que han recibido en periodos anteriores.
De acuerdo con estos resultados, solo en algunos casos específicos hay un incremento notable en la transmisión de choques en los rendimientos de los mercados analizados. No obstante, no es la única forma en la que se encuentran relacionados, como puede ser el caso de la interacción que se registra en sus volatilidades, por lo que una mayor investigación que considere las interrelaciones entre estas últimas es una tarea que está pendiente y que puede arrojar mayor luz para comprender la forma en que se propagan los choques entre estos mercados.
5. Conclusiones
En este trabajo se realizó un análisis de las relaciones entre el MILA y el S&P500. Primero se consideró el índice del MILA y se continuó el análisis con los índices de cada uno de los mercados que lo integran. Se empleó la metodología de construcción de índices de derrames propuesta por Diebold y Yilmaz (2009a, 2009b, 2012), que permite analizar la forma en que se propagan los choques en los rendimientos accionarios de esos mercados para entender sus relaciones desde la perspectiva de la conectividad.
Se corrobora la importancia del mercado estadounidense por ser uno de los principales contribuyentes a la presencia de derrames en los mercados del MILA. Entre los diferentes mercados de la región, se observan influencias diferenciadas sin un mercado dominante. En términos de posibilidades de inversión de portafolio, se puede concluir que los mercados del MILA pueden ofrecer oportunidades de diversificación con diferentes grados de exposición a los efectos de contagio por spillovers del mercado estadounidense. El análisis de esas posibilidades va más allá del análisis planteado en este trabajo, que, naturalmente, al ser materia de estudio por sí mismo se sugiere como una línea de investigación futura.
Llama la atención que en los primeros meses de 2020 (periodo del estudio relacionado con la pandemia de la COVID-19) no se hayan incrementado de manera importante los índices de spillover, a pesar del incremento en la incertidumbre que experimentaron esos mercados en dicho periodo y que se tradujo en un nivel de mayor volatilidad. Este resultado parece interesante en términos prácticos, pues podría sugerir que los grandes choques en el principal mercado de valores del continente no necesariamente afectan de manera automática a todos los mercados.
Es importante estudiar más profundamente las relaciones entre los mercados del MILA, así como la relación de este bloque con otros mercados del mundo. Para entender mejor el proceso de integración de los mercados que forman parte del MILA, es necesario analizar las características económicas de los países, así como los vínculos económicos entre estos. Es claro que la profundidad requerida por esos estudios va más allá del interés inmediato y enfoque principal del presente trabajo, por lo que se deja para la agenda de investigación futura.