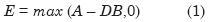
APROXIMACIÓN DE RECLAMOS CONTINGENTES PARA LA PREDICCIÓN DE RIESGO DE CRÉDITO EN SUS MEDIDAS DE DETERMINACIÓN DE LA DISTANCIA DE DEFAULT Y SU PROBABILIDAD DE QUIEBRA PARA COLOMBIA1,2
JUAN SERGIO CRUZ MERCHÁN*1, JAIME VARGAS VIVES2
1Magíster en Política Internacional, Universidad Politécnica de España, España. Profesor, Universidad Nacional de Colombia, Colombia. Investigador, Centro de Investigaciones para el Desarrollo (CID), Colombia. juacruz2009@gmail.com
2Candidato al título de Especialista en Finanzas, Colegio de Estudios Superiores de Administración (CESA), Colombia. Gerente Financiero, Superior, Colombia. jaimevargasvives@hotmal.com
* Autor para correspondencia. Dirigir correspondencia a: Calle 87 No 19c-41 Apto 302, Bogotá, Colombia.
Fecha de recepción: 04-09-2009 Fecha de corrección: 15-07-2010 Fecha de aceptación: 11-01-2011
RESUMEN
El propósito de este artículo es evaluar el grado de aplicabilidad de la ruptura -Black y Scholes (1973) y Merton (1974)- en el mercado de valores de Colombia, desde la aproximación de reclamos contingentes, dentro de la nueva coyuntura del ciclo económico para América Latina. En particular, se examinará la habilidad de la Aproximación de Reclamos Contingentes desde la perspectiva de KMV Moody's, para estimar dos indicadores de riesgo de crédito: la distancia de bancarrota y la probabilidad de default, y luego comparar estas medidas con las que produce el mercado. Los resultados sugieren la posibilidad de uso de este modelo en Colombia, en especial para las empresas que no cotizan en bolsa.
PALABRAS CLAVE
Reclamo contingente, indicadores de quiebra, distancia de default.
Clasificación JEL: G13
ABSTRACT
Contingent claim approach to forecasting credit risk based on measurements of the distanceto-default and the probability of bankruptcy in Colombia
The purpose of this article is to assess the extent of applicability of bankruptcy - Black and Scholes (1973) and Merton (1974) - to the securities market in Colombia using the contingent claim approach in the context of the new current economic cycle in Latin America. It particularly examines the ability of the contingent claim approach, from the perspective of Moody’s KMV, to estimate the two following credit risk indicators: distance to bankruptcy and probability of default. It then provides a comparison of these measurements versus those generated by the market. The findings suggest that there is a possibility of using this model in Colombia, especially with non-listed companies.
KEY WORDS
Contingent claim, bankruptcy indicators, distance-to-default.
RESUMO
Abordagem de créditos condicionais para a previsão de riscos de crédito em suas medidas de determinação da distância de default e sua probabilidade de quebra para a Colômbia
O objetivo desse artigo é avaliar o grau de aplicabilidade da ruptura - Black e Scholes (1973) e Merton (1974) - no mercado de ações da Colômbia, a partir da abordagem de créditos condicionais, no novo contexto do ciclo econômico para a América Latina. Nomeadamente, se examinará a capacidade da abordagem dos créditos condicionais na perspectiva de Moody’s KMV, para estimar dois indicadores de risco de crédito: a distância da falência e a probabilidade padrão, e em seguida comparar essas medidas com aquelas causadas pelo mercado. Os resultados sugerem a possibilidade de usar esse modelo na Colômbia, em especial para as empresas não cotadas em bolsa.
PALAVRAS-CHAVE
Créditos condicionais, indicadores de falência, distância padrão.
INTRODUCCIÓN
La agudización de la crisis económica que enfrentarán los países de América Latina en esta coyuntura internacional, exige el desarrollo y la implementación de nuevas prácticas frente al riesgo de crédito por parte de los inversores institucionales y personas naturales. Esto conlleva que se trabaje con rapidez3 en la construcción de nuevos indicadores de quiebra que recojan las expectativas de los agentes del mercado y supere así el retraso de la información contable anual.
Las aplicaciones de modelos lineales fueron métricas insuficientes y forzaron a implementar nuevas vertientes teóricas de riesgo de crédito (Altman, 1968). Como resultado, desde los años ochenta, muchos estudios se han concentrado en desarrollar los espacios de las consecuencias de la ruptura de 1973 y hoy se pueden dividir estos trabajos en dos líneas: modelos estructurales y formas reducidas (Teixeira, 2007). Esta investigación se centra en la primera línea.
El objetivo de esta investigación es, en primer término, desarrollar la Metodología de Reclamos Contingentes dentro de la línea académica y comercial de Moody´s y Vasicek con su modelo Expected Default Frecuency (EDF)4 y determinar su grado de aplicabilidad en Colombia. Este documento entiende por grado de aplicabilidad las modificaciones teóricas y prácticas que se requieren acometer para llegar a un resultado, dentro de unos lineamientos teóricos de las finanzas que le den sentido a los números.
En segundo término, se realizará un comparativo con las calificaciones de las emisiones de bonos de las empresas seleccionadas del mercado público de valores, con el fin de probar si las tendencias de las dos medidas -los resultados de la investigación y las del mercado- son coincidentes o no. Esta inquietud surge porque las calificadoras de riesgo fueron unas de las instituciones cuestionadas en la actual crisis del mercado hipotecario norteamericano e internacional; es así como Europa divulgó un documento sobre regulación a las calificadoras de riesgo (Gonzalez, 2009). De acuerdo con Crouhy, Galia y Mark (2001) y Rodríguez (2004) ellos sostienen que:
Para la consecución de estos dos objetivos este documento se organizó de la siguiente forma. El artículo empieza con esta primera sección introductoria, donde se precisa el alcance del estudio. La primera sección hace una presentación esquemática de la literatura relacionada desde 1973 hasta agosto de 2009 y ofrece así un marco teórico/explicativo de las secciones siguientes. La segunda sección presenta la metodología de reclamos contingentes desde una perspectiva conceptual. Aquí se busca que el lector no se enrede con el lenguaje matemático sino que se concentre en su significado. La tercera sección hará la presentación de la Metodología de EDF con su debida formalización matemática. En este artículo no se hará ninguna demostración matemática porque ha sido terreno fértil de otros trabajos, sino que más bien, se centrará en los objetivos precisos de este artículo. En la cuarta sección se presentarán los resultados de la aplicabilidad de este modelo en Colombia, desde la muestra que se tomó de la Bolsa de Valores de Colombia en los últimos tres años y que recoge la fase final del crecimiento económico y la última información disponible al cierre del segundo trimestre del 2009. Por último, se presentarán las conclusiones y propuestas de nuevas líneas de investigación, en especial de empresas que no cotizan en bolsa y que requiere la re-conceptualización del modelo básico.
1. REVISIÓN BIBLIOGRÁFICA
El modelo propuesto por Merton (1974) es la base de la corriente de modelos estructurales de la valoración de la deuda corporativa. Se basa en la perspectiva de Reclamo Contingente abierta por Black y Scholes (B-S) en 1973. Es desde allí que Merton presenta a la comunidad académica un modelo muy sencillo que puede ser usado para la valoración (pricing en inglés) de cada uno de los instrumentos de la estructura financiera.
Desde un marco general, el proceso de default de una compañía está determinado por el valor de sus activos y así mismo el riesgo de default de una compañía está directamente relacionado con la variabilidad del valor de los activos. La vertiente de los modelos reducidos en contraposición no condiciona el default al valor de los activos. Merton (1974) asume que la dinámica del valor de un activo Vt, puede ser descrita a través de un proceso de difusión desde una ecuación diferencial estocástica. En su versión original, la empresa se financia con deuda y acciones que no reparten dividendos pero este supuesto se ha relajado en posteriores trabajos. Para él, el valor de la firma y de los activos es igual y no depende en sí mismo de la estructura financiera. El valor de los activos, Vo, es igual a la suma de los instrumentos que componen la estructura financiera. De la misma manera, el valor del patrimonio es igual a la diferencia entre el valor de los activos y el valor de mercado de la deuda. Desde esta perspectiva, el patrimonio puede ser visto como una opción call del valor de la firma, con un precio de equilibrio igual al valor facial de la deuda (Teixeira, 2007).
En este sentido, los principales exponentes de la ampliación del trabajo seminal de Black y Scholes (Anderson y Sundaresan, 1996; Collin-Dufresne, 2001; Fan y Sundaresan, 2000; Geske, 1977; Leland, 1994; Longstaff y Schawartz, 1995; Mella-Barral y Perraudin, 1997; y en especial, Teixeira, 2007) buscaron aproximar el marco general a la realidad. Para los propósitos específicos de la modelación matemática que se desarrollará en la sección quinta, se incluirán los aportes y presiones de los profesores Kealhofer (2003) y Vasicek (1977), quienes desarrollaron una aproximación de riesgo de crédito a partir de los conceptos básicos de B-S.
2. METODOLOGÍA
La teoría inicial de los reclamos contingentes se focalizó en la valoración de opciones y la aplicación de la teoría de las opciones al análisis de la estructura del capital corporativo.5 El valor total de una compañía está dado por la suma del valor de los securities que tenga en su estructura de capital. Estos securities pueden ser vistos como reclamos contingentes del valor implícito de la compañía. Los reclamos contingentes (CCA, por sus siglas en inglés, Contigent Claim Approach) pueden ser implementados para analizar cómo cambia el valor de los reclamos contingentes a medida que cambia el valor de la compañía a través del tiempo. Es por lo anterior que el análisis de reclamos contingentes debe ser visto como una generalización de la teoría de la valoración de opciones, con el fin de explicar el preámbulo en el cual todos los reclamos contingentes pueden ser valorados.
El análisis de reclamos contingentes se basa en tres principios: 1. El valor de los flujos del pasivo desde los activos, 2. Los pasivos tienen madurez diferente y por ende los riesgos relacionados son diferentes de acuerdo con su madurez, y 3. Existe un elemento aleatorio respecto a la forma como el valor del activo evoluciona a través del tiempo. La deuda es un reclamador antiguo del valor de los activos y el patrimonio es un reclamador junior del valor del activo. La deuda es riesgosa porque el valor del activo puede no ser suficiente para cubrir los pagos de deuda contraídos. Debido a esto, el valor de la deuda riesgosa puede ser visto con dos componentes: el valor libre de probabilidad de no pago y la pérdida esperada asociada con el no pago cuando los activos son insuficientes para cubrir los pagos de deuda contraídos. El valor de los reclamos junior (patrimonio en el caso de las compañías) se deriva del valor residual después de que se hayan hecho las promesas de pago de deuda.
Si el valor de los activos tiene un componente variable (por ejemplo, el precio cambia, shocks y otros factores que afectan el valor de los activos), cuanto más alta sea la volatilidad de los activos, mayor probabilidad de que el valor de los activos caiga por debajo del nivel necesario para cubrir los pagos de las deudas maduras a través del periodo horizonte. En consecuencia, ceteris paribus, una mayor volatilidad implica tener una pérdida esperada mucho más alta y un menor valor de deuda riesgosa. Las técnicas financieras como option pricing relationships han sido desarrolladas para medir la pérdida esperada como función del valor de los activos, de su volatilidad, la deuda libre de no pago (default) y el tiempo de horizonte. De la misma forma el valor del patrimonio y de los reclamos junior pueden ser medidos en función de las mismas variables. La pérdida esperada en la deuda riesgosa es una opción put implícita. El patrimonio y los reclamos junior son opciones call implícitas.
La esencia de los reclamos contingentes es que los cambios en las variables observadas (el valor de los securities en la estructura de capital) son usados para inferir cambios en las variables no observadas (el valor de la compañía). La aplicación de esta metodología a la estructura de capital deriva de los pasivos maduros en la estructura de capital y en la identidad del balance en que el valor del mercado de toda la deuda más el patrimonio debe ser igual al valor actual de la compañía en el mercado. Dado que el patrimonio representa un reclamo residual sobre los activos, con pasivos limitados, este se puede modelar como una opción call. La característica de default le permite al tenedor entregar el activo subyacente en forma de pago de la deuda si el valor de este cae por debajo del valor de la deuda. En este caso el activo subyacente es el valor de los activos o valor de la firma. En otras palabras el accionista puede irse si el valor de la compañía cae por debajo del valor de la deuda. El pago de deuda a su madurez es equivalente a la diferencia entre el valor libre de no pago (libre de default) y una opción put en el valor de la compañía con el strike-price igual al valor en libros de la deuda y su fecha de expiración equivalente a la madurez de la deuda. La opción put representa el reclamo limitado de pasivos suscrito por el tomador de la deuda para con el socio, lo que le da a este último la libertad de someter los activos de la compañía e irse cuando su valor caiga por debajo de los pagos prometidos del tomador de la deuda a la madurez.
2.1. La metodología de reclamos contingentes (Gapen, Gray, Lim y Xiao, 2004)
En este apartado se ilustra la metodología de reclamos contingentes (CCA) aplicada a un balance simplificado de una compañía comprometida con deuda madura y patrimonio junior. En algún punto del tiempo, el valor total de mercado de los activos A de una compañía financiada con deuda D y patrimonio E, es igual al valor de mercado del patrimonio más el valor de mercado de la deuda riesgosa. El análisis fundamental establece que el valor de los activos de la compañía se deriva de un proceso estocástico del valor presente descontado del ingreso menos los gastos, con el potencial de que el valor de los activos caiga por debajo del punto en el cual los pagos programados de deuda puedan ser hechos. Si los activos caen por debajo del nivel en el cual la deuda no pueda ser servida, el no pago (default) es el resultado. Este nivel es comúnmente conocido como Distress Barrier (DB o barrera de punto de quiebra, por su traducción al español), y es igual a o cercano al valor de la deuda libre de no pago (libre de default).
Los socios tienen un reclamo contingente junior sobre el valor residual de los activos en el futuro. De este modo, el valor del patrimonio puede ser visto como una opción en la cual los socios reciben el máximo de los activos menos DB, o nada en caso de default. El valor del patrimonio por ende es como en la Ecuación 1:
Las fórmulas estándar del option pricing pueden ser usadas para relacionar los cambios en el precio de la compañía a los cambios en el patrimonio. Dada la relación que hay entre el patrimonio de la compañía y sus activos, los cambios en el valor del patrimonio transado pueden ser usados a través de las relaciones del option pricing para inferir los cambios en el valor del mercado de los activos de la compañía.
Sin embargo, en el caso de la deuda riesgosa todo es un poco más complejo. Los acreedores de la deuda están obligados a absorber las pérdidas en caso de no pago (default) y la garantía de repago por el deudor puede ser modelada como una opción put implícita dado que los acreedores reciben los activos de la compañía que no pague (o de forma equivalente los activos de la compañía son puestos a disposición de los acreedores). Por ende, los acreedores de deuda riesgosa reciben el mínimo del valor libre de default, o en el caso de default, el reclamo maduro en los activos. Desde que el valor de la deuda libre de default es igual al DB y a la opción implícita put de los activos la compañía (DB – A,0), el valor de la deuda riesgosa puede ser modelado en la Ecuación 2:
Si se insertan estas relaciones de option pricing a la identidad del balance, resulta en que un valor de mercado de la compañía en un instante de tiempo t, se define como:
La fórmula de option pricing es usada en dos pasos. Primero, el valor observado de mercado del patrimonio y el DB son usados con la fórmula de la opción call para derivar el valor de los activos de la compañía. El valor de los activos de la compañía y el DB son usados luego con la fórmula de la opción put para derivar el valor implícito de mercado de la deuda riesgosa. Por ende el CCA usa las fórmulas put y call del option pricing para desarrollar un balance al valor del mercado sobre las variables financieras del mismo.
2.2. Distancia default y la probabilidad de default
Los dos indicadores más útiles de crédito riesgoso que surgen de la implementación del CCA son la distancia al DB y la probabilidad de default. Las fórmulas de option pricing aplicadas en el CCA recaen sobre pocas variables seleccionadas: el valor implícito de los activos, la volatilidad implícita de los activos, el DB, la tasa de interés libre de riesgo y el tiempo. Estas variables pueden ser combinadas en una única medida del riesgo de default. Esta medida que se llama la distancia al DB, compara la diferencia entre el valor de mercado de la compañía relativo al DB y luego escala esta distancia basado en la volatilidad de los activos. En la aplicación del CCA a la estructura actual del capital de la compañía, muchos practicantes computan el DB como suma del valor en libros de la deuda de corto plazo y la mitad de la deuda de largo plazo más los intereses de la deuda de largo plazo. Esta computación se usa dado que las instancias de default de las compañías han demostrado que es posible que el valor transado de los activos caiga incluso por debajo del valor en libro del total de la deuda para periodos significativos sin defaults si la mayor parte de la deuda es a largo plazo. Sin embargo, la deuda a corto plazo está más ligada, dado que la compañía enfrenta riesgo en un periodo menor. Por ende, se hace un ajuste para reducir el peso de la deuda a largo plazo en el DB.
La distancia al DB combina la diferencia entre los activos y el DB con la volatilidad de los activos en una única medida, como en la Ecuación 5, lo que incluye el número de desviaciones estándar del valor de los activos del DB. El numerador mide la distancia entre el valor de mercado proyectado a un año de los activos de la compañía y el DB. Esta cantidad luego es escalada por un movimiento de una desviación estándar en los activos de la compañía. A niveles bajos del valor de los activos en el mercado, mayores niveles de apalancamiento y mayores niveles de volatilidad, se reduce la distancia al DB.
El paso final para determinar la probabilidad de default consiste en hacer un mapeo entre las distancias de medida de DB de la Ecuación 5 y las probabilidades actuales de default basadas en datos históricos. Usando información histórica de una gran muestra de compañías y estableciendo una medida determinada de distancia a DB, el modelo de Moody’s KMV es capaz de estimar la proporción de estas compañías, que de hecho hicieron default en un año adelante en el horizonte de tiempo.
3. METODOLOGÍA DE EXPECTED DEFAULT FREQUENCY (EDF) Y SU REPRESENTACIÓN MATEMÁTICA
Como se afirmó en la sección inicial, esta investigación parte de los desarrollos matemáticos de las escuelas norteamericanas para centrarse en determinar el grado de aplicabilidad del modelo a las condiciones del mercado público de valores en Colombia. Para tal efecto, se recoge la formulación matemática de Crosbie y Bohn (2003) cuyo desarrollo fue traducido en la tesis de grado de Rodríguez (2004). Lo importante de este trabajo numérico es tener claros los supuestos de los diferentes modelos y su posibilidad práctica en Colombia, máxime la restricción y consistencia de la información. No obstante, se tiene reparos en la determinación de uno de los parámetros claves de la modelación pero que no invalida para nada el modelo y se calculó de forma diversa.
La metodología debe seguir una serie de pasos que son:
Este punto no significa que la empresa no siga operando, en Colombia, la mayoría de las empresas que entraron al proceso de la Ley de Bancarrota en Colombia y de default de la Superintendencia de Sociedades, ya habían superado este punto hace un buen tiempo (Cruz, 2009) (ver Anexo 1).
La distancia default (ver Ecuación 7) es una medida en términos de desviaciones estándar de la media hasta el punto de la bancarrota que combina tres llaves en el tema de riesgo: el valor de los activos de firma, el riesgo de la empresa y el riesgo de la industria. Igualmente, esta medida incorpora, a través de la volatilidad y el valor de los activos, los efectos de la industria, la ubicación geográfica y el tamaño.
De lo anterior se concluyen dos ecuaciones que permiten calcular el valor de mercado de los activos y su volatilidad, que son dos variables desconocidas hasta el momento a partir de los otros valores:
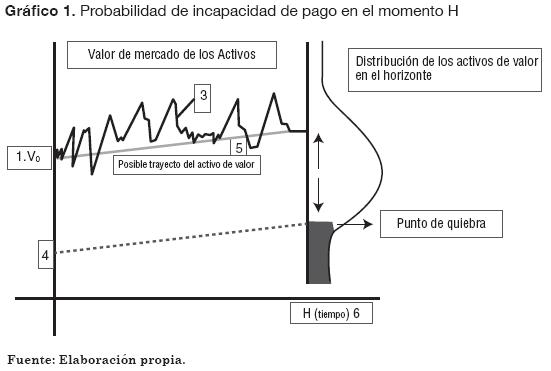
Donde:
Para parametrizar el modelo y su posterior aplicación en empresas colombianas se define la siguiente estructura básica financiera:
Se establecerá un tiempo inicial como tiempo 0 y un tiempo T que corresponde al vencimiento o madurez de la deuda de corto plazo. Este plazo se asumirá también como vencimiento de las obligaciones corrientes. El valor a amortizar de la deuda de corto plazo en el tiempo T se denotará por CT.
Se asume que:
3.1. Punto de bancarrota
En la sección anterior se estableció que el precio del ejercicio para las opciones call y put corresponde a las deudas que disparan la bancarrota. En este caso, esas deudas corresponden a las de corto plazo C y a las obligaciones corrientes O, por lo tanto se define el punto de bancarrota como en la Ecuación 8:
Adicionalmente, Ogden (1987) establece que el punto de quiebra de una compañía es aproximadamente la suma de las deudas de corto plazo y la mitad de las de largo plazo. De lo cual se concluye que las obligaciones corrientes en la práctica se estiman como la mitad de las deudas de largo plazo.
3.2. Valor de mercado de los activos como proceso estocástico
Una forma de describir el comportamiento de los activos de una compañía es especificar que los cambios porcentuales de estos son independientes del pasado, es decir, únicamente dependen de su estado actual (propiedad de Markov).6
De acuerdo a esto, los activos se pueden modelar mediante el siguiente proceso estocástico conocido como movimiento Browniano simple:7
Donde dA representa el cambio en los activos, A representa los activos en el tiempo T, μ representa los retornos de la compañía, σA la varianza instantánea sobre los retornos de los activos de la compañía y i corresponde al proceso de Wiener8 (un tipo de proceso markoviano con cambios en la media iguales a 0 y varianza igual a 1 por unidad de tiempo). De esta manera, el comportamiento del retorno de los activos constituye una parte determinística o de tendencia (μAdt) que corresponde a la media, y una parte aleatoria o variable que corresponde al segundo término de la ecuación (μAdz)
Se asume que el rendimiento de los activos es la prima que deben pagar las compañías sobre la tasa libre de riesgo que recompense a los inversionistas por el exceso de riesgo. Al ser no observables los activos, el cálculo de este parámetro es difícil de estimar. De acuerdo con las metodologías de Creditmetrics y CreditVar (Elizalde, 2003), μ se puede estimar como el equivalente al rendimiento del patrimonio para el periodo inmediatamente anterior a T. Esto se representa en el Gráfico 1 como la tasa a la que se espera renten los activos después de un año. Se asumirá que en el tiempo 0 se realizará el prepago de los dividendos e intereses sobre la deuda, proyectados durante el periodo T. Este flujo negativo se denotará como F:
Un gran aporte que posteriormente Black-Scholes y Merton utilizaron para la derivación de su ecuación diferencial fue el conocido Lema de Itô. Este establece que para el proceso descrito por la Ecuación 9, debe existir una función G de los activos A y del tiempo t que siga el siguiente proceso:9
Donde G también sigue un proceso de Wiener. Luego se construye un portafolio con la cantidad apropiada de A derivado (dG) y de activo subyacente de las Ecuaciones 9 y 11 y así poder eliminar dz de la ecuación.10 Entonces, el portafolio se confirma con (-1) derivados y (+ ∂G/∂S)activos subyacentes y se obtiene:
Esta es la ecuación de Black – Scholes – Merton que permite encontrar la valoración del derivado G de acuerdo con las condiciones de borde que se incluyan. En el modelo r corresponde a la tasa de retorno libre de riesgo que hace que en el derivado no pueda existir arbitraje durante un periodo infinitesimal t. Con base en esta ecuación, las soluciones que se encuentran para las condiciones de borde de los derivados: opciones call y put son respectivamente:Donde:
De acuerdo con esto, S(0) en el modelo EDF, corresponde a los activos en el tiempo cero [A(0) – F], el precio de ejercicio K corresponde a las deudas que disparan la bancarrota o también definido como punto de bancarrota [CT + OT] . Las valoraciones para la opción call (patrimonio) y la opción put (vender deuda) con las consideraciones anteriores son:
Donde
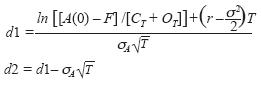
E Se define como el valor de la opción call (patrimonio)
P Se define como el valor de la opción put
r Representa la tasa libre de riesgo
3.3. Estimación de la volatilidad de los activos
De la Ecuación 17 se puede derivar una segunda ecuación, la cual explica la relación existente entre la varianza del patrimonio σE y la de los activos σA:
La relación se puede ver como la
elasticidad del patrimonio con los activos, es decir, la cantidad porcentual
del cambio del patrimonio al cambio
en 1% del cambio de los activos. La
estimación de la volatilidad del patrimonio mediante la Ecuación 19 se
mantiene solo de forma instantánea.
Por ende, la Ecuación 19 resulta en:
se puede ver como la
elasticidad del patrimonio con los activos, es decir, la cantidad porcentual
del cambio del patrimonio al cambio
en 1% del cambio de los activos. La
estimación de la volatilidad del patrimonio mediante la Ecuación 19 se
mantiene solo de forma instantánea.
Por ende, la Ecuación 19 resulta en:
Teniendo en cuenta las Ecuaciones 17 y 20 se puede ver que existen dos variables desconocidas, el valor de los activos A(0) y su volatilidad σA; es decir, se tienen dos ecuaciones con dos incógnitas, por lo tanto se pueden encontrar las soluciones correspondientes.
Sin embargo, la volatilidad como se define en la Ecuación 20 tiene varios inconvenientes para aplicarla a un modelo real. Según Crosbie y Bohn (2003) es aquí donde hay fuertes discrepancias con los autores citados, porque no se encuentra una solución analítica y la revisión reciente de la literatura afirma lo mismo (Jara, 2001; Laciana, 2004). Jara sostiene que no se puede calcular la volatilidad implícita y que se requiere un método de aproximación del tipo de Newton-Rapson. Igualmente, Laciana piensa que:
3.4. Distancia a bancarrota
Una vez conocido el valor de mercado de los activos y su volatilidad, se calcula la distancia a bancarrota, la cual representa, como se mencionó en la sección 2, la proximidad al punto de bancarrota como el número de desviaciones estándar. Esta medida se representa como:
Ahora, incorporando las especificaciones del modelo descritas anteriormente se tiene,
Esta representa la ecuación que se utilizará para el cálculo de la distancia a bancarrota de las empresas colombianas en la siguiente sección.
3.5. Probabilidad de bancarrota
La probabilidad de bancarrota como se definía en la sección anterior, se refiere a la posibilidad de que los activos caigan a un valor menor al punto de bancarrota, es decir,
Donde A(T) son los activos en el tiempo T. Las demás variables deberían ser familiares. Por lo tanto, tomando el logarítmico natural a ambos lados,
Recordando que el logaritmo de los activos se distribuye normalmente (Ecuación 12), la probabilidad descrita en la Ecuación 24 es:
Donde N representa la función de distribución acumulada normal.
En este sentido, la probabilidad de bancarrota utilizando el modelo EDF se puede encontrar empleando la Ecuación 25. Sin embargo, estos estudios realizados por KMV, demuestran que la probabilidad de quiebra no puede mantener el supuesto de normalidad. Kealhofer (2003) establece que una compañía que se encuentra a más de cuatro desviaciones estándar de su punto de bancarrota tendría (en el caso de distribución normal) esencialmente probabilidad cero de bancarrota. Actualmente esta probabilidad (para las compañías estadounidenses) es cercana al 0,05%. Por esta razón, la probabilidad determinada por esta distribución no es aplicable en la práctica.
Según Crosbie y Bohn (2003) es necesario calcular una distribución empírica, la cual se base en tomar la distancia a bancarrota DB como estadístico suficiente que posea el poder de explicación de la probabilidad de bancarrota. En la práctica no es posible encontrar una función de distribución en Colombia porque se carece de los datos requeridos. No hay que confundir las empresas que se quiebran y que están bajo la competencia de Supersociedades ya que estas no cotizan en Bolsa. Significa esto que no se puede usar los estimadores de quiebra de aquellas que no cotizan en Bolsa y, si se hace, se debe ser muy cuidadoso en la argumentación en su defensa.
4. RESULTADOS
Para la determinación de la muestra se tomaron las empresas que cotizan en el mercado público de valores con un grado de transacción, el resultado inicial fue de 23 compañías. Esta condición busca garantizar que los precios reflejen condiciones de mercado. De esa muestra se retiraron las empresas del sector financiero, ya que la base de datos de liquidadas y reestructuradas con que cuenta la investigación son del sector real. Luego se tomaron las empresas que tienen un grado de exposición por comercio exterior. Por último, se seleccionaron aquellas empresas que hayan emitido deuda con el fin de comparar la dinámica de la calificación que ofrece el mercado y la que se obtiene con el modelo. Las empresas resultantes son once: Cementos Argos, Compañía Nacional de Chocolates, Colombiana de Inversores, Coltejer, Enka, Éxito, Fabricato, Inverargos, Mineros, Tablemac y Valorem. No obstante, se presentan los resultados de cuatro empresas.
Con el fin de determinar el grado de aplicabilidad del modelo, se partió del primer trimestre del 2007 donde aún se manifestaba un crecimiento económico. Igualmente, se tomaron trimestres porque la información que reporta Superfinanciera está expresada en esos términos y, a su vez, para medir la dinámica del modelo en diferentes momentos del año.
La información utilizada fue:
Con la información anterior se procedió a calcular el precio de mercado del patrimonio. Esto fue posible porque hay evidencias empíricas sobre la asignación de precio a un conjunto de empresas que cotizan en bolsa. No obstante, la siguiente investigación se centrará en desarrollar un modelo de riesgo de crédito para empresas que no cotizan en Bolsa dentro de la línea de investigación de Crosbie y Bohn (2003) y sus posteriores modificaciones por parte de los autores. Luego, con el valor de mercado del patrimonio, se procedió a calcular el valor de mercado de la deuda. Como no todos los instrumentos de la estructura financiera son valorados en el mercado, se procedió a seguir el algoritmo que se explicó en la sección anterior. Con este último parámetro se calculó el valor de los activos en el momento inicial (Vo) como la suma del valor de mercado del patrimonio y de la deuda. Luego se hizo la pregunta ¿cuál es la tasa promedio de crecimiento de los activos (Ua) a valor de mercado? Está claro que no hay una evidencia empírica de este parámetro, por lo que debe ser estimado de forma indirecta.
Para datos históricos se tomó la variación del valor del patrimonio a precios de mercado y para su estimación futura se tomó la tasa forward del yield de las acciones como la relación de los dividendos estimados para el siguiente periodo D1 y el precio de la acción hoy P0 (CFA Institute, 2009). Para llegar a este pronóstico se tomó el crecimiento promedio de los dividendos de los dos últimos años. No obstante, esta cifra puede ser significativa o no dependiendo de la tradición de repartición de dividendos de cada empresa y las percepciones habituales de rendimiento de los accionistas. Con este parámetro de crecimiento o decrecimiento de los activos y con el valor de los activos en el momento cero y en cualquier momento del tiempo, se calculó la volatilidad del activo. No se calculó el valor del activo a precio de mercado en el momento de cero y su volatilidad como lo propusieron Crosbie y Bohn (2003) sino que se calculó el valor de Vo como la suma de los valores del patrimonio y de la deuda a precios de mercado y posteriormente se calculó la volatilidad de los activos. A partir de allí se usaron el conocido modelo de B-S y las ecuaciones de distancia de bancarrota (Ecuación 22) y de probabilidad de default (Ecuación 25).
Se presentan los resultados de las empresas de Tablemac, Cementos Argos, Éxito y Nacional de Chocolates.11 Recuerde que hay dos objetivos en el presente artículo: en primer término, desarrollar la metodología de reclamos contingentes dentro de la línea académica y comercial de Moody's y Vasicek con su modelo Expected Default Frecuency (EDF) (Crosbie y Bohn, 2003) y determinar su grado de aplicabilidad en Colombia. En segundo término, se realizará un comparativo con las calificaciones de las emisiones de bonos de las empresas seleccionadas del mercado público de valores con el fin de medir si las tendencias de las dos medidas -los resultados de la investigación y las del mercado- son coincidentes o no.
Para el primer objetivo se presenta la Tabla 1, la cual resume los resultados de la modelación de la distancia de bancarrota y la probabilidad de bancarrota de la compañía Tablemac que cotiza en bolsa. La tabla está estructurada en tres columnas. La primera columna es el parámetro, la segunda columna es la presentación y/o explicación de cómo se obtuvieron las cifras que están en la tercera columna. Se considera que esta transparencia cumple con uno de los objetivos que es el de velar por la aplicabilidad, lo cual es posible si se presenta el modelo de forma abierta y transparente, para su discusión en diferentes ámbitos. Como ejemplo, al modelar el tercer trimestre del presente año y los resultados de acuerdo con el modelo de EDF para Colombia, se encuentra que la probabilidad de quiebra es igual a cero. Lo importante de este apartado no es la cifra misma sino los supuestos que se tuvieron que hacer para la aplicación del modelo en Colombia. Es por ello que se invita a leer cada una de las filas de la Tabla 1.

En la Tabla 2 se presentan los resultados más significativos del modelo EDF para la compañía Tablemac, mostrando los resultados de cada una de las empresas mencionadas con anterioridad. Más adelante se presentarán los modelos para las compañías Argos (ver Tabla 3), la compañía Éxito (ver Tabla 4) y la Compañía Nacional de Chocolates (ver Tabla 5).
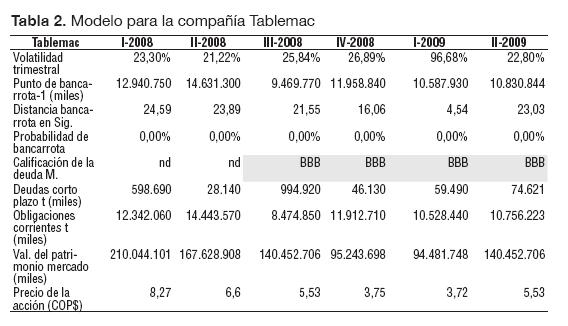



Como se puede apreciar en las Tablas 2 a 5, la probabilidad de quiebra tiende a 0% para cada una de las empresas. Sin embargo, esto no quiere decir que ninguna de estas empresas se quebrará, ni que en el tiempo la probabilidad de quiebra es igual a 0. Lo que quiere decir este resultado, es que la probabilidad de quiebra en el periodo T+1 de cualquiera de las cuatro empresas mencionadas, es efectivamente igual a 0%. Esto en gran parte se debe al muy bajo nivel de endeudamiento de cada una de estas empresas junto al muy alto patrimonio que poseen; y dada la volatilidad en el retorno de los activos es improbable (por no decir imposible) que alguna de estas empresas se encuentre en la quiebra en el periodo inmediatamente posterior, ya que tendría que existir un deterioro tal que el valor de los pasivos sea mayor al valor de los activos (patrimonio negativo). Es por ello que bajo este modelo es necesario reevaluar las calificaciones crediticias en cada periodo t de tiempo y en Colombia los Estados Financieros se actualizan trimestralmente.
Para el cumplimento del segundo objetivo de la investigación, al inicio se pensó hacer una calificación por cada una de las empresas, pero el debate de la situación llevó a no hacerlo porque se introducían criterios subjetivos que le quitaban validez a la comparación. No obstante, se continuó con el objetivo de otra forma y fue por medio de la comparación de la probabilidad de quiebra del modelo para cada una de las empresas en un periodo comparable con la calificación que da el mercado (ver Tabla 6).
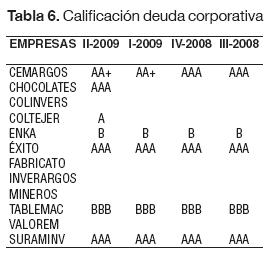
Este ejercicio se hizo de forma extensiva para todas las empresas de la muestra pero al final se redujo a las empresas de las cuales se obtuvo información de la calificación de su deuda. Si se analiza la Tabla 6, la evidencia empírica arroja que aproximadamente en el 100% de la muestra la evaluación de la deuda no ha variado excepto para la compañía Cemargos.
No obstante, los resultados de la modelación sugieren otra cosa. En la discusión se precisa el hecho en cuanto a que una compañía de las tres calificadoras de riesgo en Colombia modificó las calificaciones a la baja pero tan solo un mes después reversó la decisión, sin dar una respuesta satisfactoria al mercado. En el caso de Cemargos, se puede apreciar que aunque en el tercer trimestre del 2008 la distancia de bancarrota venía disminuyendo, su calificación es modificada a la baja en el trimestre posterior, cuando la distancia a bancarrota había aumentado significativamente. A pesar de ello, la calificación de Cemargos no se volvería a modificar.
5. DISCUSIÓN
Los resultados preliminares de este estudio sugieren que:

NOTAS AL PIE DE PÁGINA
1. Agradecimientos: a Sandra y Federico por su amor.
2. Este documento fue seleccionado en la convocatoria para enviar artículos, Call for Papers, realizada en el marco del Simposio "Análisis y propuestas creativas ante los retos del nuevo entorno empresarial", organizado en el marco de celebración de los 30 años de la Facultad de Ciencias Administrativas y Económicas de la Universidad Icesi y de los 25 años de su revista académica, Estudios Gerenciales, el 15 y 16 de octubre de 2009, en la ciudad de Cali (Colombia). El documento fue presentado en las sesiones simultáneas del área de "Finanzas".
3. Guédez (2003, p. 7) al respecto: "Senge citaba al jefe de planificación estratégica del Grupo Royal Dutch/ Shell, Arie de Guez, para quien la habilidad para aprender con mayor rapidez que los competidores pudiera ser la única ventaja comparativa sustentable".
4. En la línea de Crosbie y Bohn (2003).
5. Ver el trabajo de Gapen, Gray, Lim y Xiao (2004).
6. Las cadenas de Markov y los procesos de Markov son un tipo especial de procesos estocásticos.
7. En el año 1905, el famoso físico Albert Einstein (1879-1955) publicó un célebre trabajo en el que propuso la explicación del movimiento browniano. Es interesante notar que ese mismo año Einstein publicó otros dos famosos trabajos: el del efecto fotoeléctrico (que le valdría el premio Nobel de Física en 1923) y el de la teoría de la relatividad de la suposición atómica. En particular se interesó por las conclusiones que se obtendrían si el movimiento browniano se tratara de explicar por medio de la hipótesis atómica.
8. El proceso de Wiener es un proceso estocástico de tiempo continuo.
9. La explicación detallada de la obtención de la Ecuación 11 va más allá del objetivo principal de este artículo. Se invita al lector interesado en el tema de cálculo estocástico a consultar la referencia de Itô (1951).
10. Consideraciones hechas sobre la teoría de opciones detallada en Hull (2008, pp. 216-266).
11. Se escogieron solamente estas empresas por problemas de espacio, sin embargo, la persona interesada en la modelación de todas las empresas puede solicitar dicha información a los autores.
REFERENCIAS BIBLIOGRÁFICAS
1. Altman, E.I. (1968). Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy. Journal of Finance, 23(4), 589–609.
2. Altman, E.I. y Kishore, V. (1996). Almost everything you wanted to know about recoveries on default bonds. Financial Analysis Journal, 52(6), 57-64.
3. Anderson, R. y Sundaresan, S. (1996). Design and valuation of debt contracts. Review of Financial Studies, 9(1), 37-68.
4. Baxter, M. y Rennie, A. (1996). Financial Calculus: An Introduction to Derivative Pricing. Cambridge: Cambridge University Press.
5. Black, F. y Scholes, M. (1973). The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81(3), 637–659.
6. Bodie, Z., y Merton, R. (2000). Finance. Upper Saddle River, NJ: Prentice Hall.
7. Bohn, J.R. y Crosbie, P.J. (2002). Modeling Default Risk. KMV, LLC. New York, NY: KMV, LLC.
8. CFA Institute. (2009). CFA Program Curriculum: Level I (Vol. 4. Corporate Finance and Portfolio Management). New York, NY: Autor.
9. Collin-Dufresne, P. (2001). The determinants of credit spread changes. The Journal of Finance, 56(6), 2177-07.
10. Crosbie, P. y Bohn, J. (2003). Modeling Default Risk. New York, NY: Moody’s KMV Company. Recuperado de http://www.moodyskmv.com
11. Crouhy, M., Galai, D. y Mark, R. (2000). A Comparative Analysis of Current Credit Risk Models. Journal of Banking and Finance, 24(1-2), 59–117.
12. Crouhy, M., Galai, D. y Mark, R. (2001). Risk management. New York, NY: McGraw-Hill.
13. Cruz, J.S. (2009). The determinants of bankruptcy and default of real sector companies in Colombia for a differentiated government policy -since the economy has been officially declared to be in recession (Working Paper CESA). Bogotá: CESA.
14. Elizalde, A. (2003). Credit Risk Model II: Structural Models (CEMFI and Universidad Pública de Navarra working papers). Recuperado de http://www.abelelizalde.com/
15. Fan, H. y Sundaresan, S. (2000). Debt valuation, renegotiation and optimal dividend policy. Review of Financial Studies, 13(4), 1057-99.
16. Gapen, M.T., Gray, D.F., Lim, C.H. y Xiao, Y. (2004). The Contingent Claims approach to Corporate Vulnerability Analysis: Estimating Default Risk and Economy wide Risk Transfer (IMF working paper). Recuperado de http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.139.648&rep=rep1&type=pdf
17. Geske, R. (1977). The valuation of corporate liabilities as compound options. Journal of Financial and Quantitative Analysis, 12(4), 541-52.
18. Geske, R. (1979). The Valuation of Compound Options. Journal of Financial Economics, 7(1), 63–81.
19. González, R. (2009, 28 de agosto). Pese a la crisis financiera, el 94% de las calificaciones se mantiene, dice el Presidente de BRC Investor [versión electrónica]. Portafolio. Recuperado de http://www.portafolio.com.co/archivo/documento/CMS-5967271
20. Gray, D. (2001). Macro Financial Risk Country Report. MfRisk (Reporte técnico pendiente de patente).
21. Guédez, V. (2003). Aprender a emprender. De la gerencia del conocimiento a la ética de la sabiduría. Caracas, Venezuela: Planeta.
22. Hull, J.C. (2008). Option, Futures and Other Derivatives. Englewood Cliffs, NJ: Prentice Hall.
23. Itô, K. (1951). On Stochastic Differential Equations. Memoirs of the American Mathematic Society, 4, 1-51.
24. Jara, J.R. (2001). Análisis empírico del modelo de valoración de BlackScholes mediante el modelo generalizado de los momentos: una aplicación a las opciones sobre Ibex-35. Revista Española de Financiación y Contabilidad, 30(110), 939-972.
25. Jones, E., Masson, S. y Rosenfeld, E. (1984). Contingent Claims Analysis of Corporate Capital Structures: An Empirical Investigation. Journal of Finance, 39(3), 611–625.
26. Kealhofer, S. (2003). Quantifying Credit Risk II: Debt Valuation. Financial Analysts Journal, 59(3), May/June.
27. Laciana, C. (2004). Modelos matemáticos para la valoración de opciones financieras. Informe de FIUBA-LMM RA01-01-2004. Manuscrito no publicado, Facultad de Ingeniería, Universidad de Buenos Aires.
28. Leland, H.E. (1994). Corporate debt value, bond covenants and optimal capital structure. Journal of Finance, 49(4), 1213-52.
29. Longstaff, F. y Schawartz, E. (1995). A Simple Approach to Valuing Risky Fixed and Floating Rate Debt. Journal of Finance, 50(3), 789-820.
30. Mella-Barral, P. y Perraudin, W. (1997). Strategic debt service. Journal of Finance, 52(2), 531-66.
31. Merton, R. (1973). Theory of Rational Option Pricing. Bell Journal of Economics and Management Science, 4(1), 141–83.
32. Merton, R. (1974). On the Pricing of Corporate Debt: The Risk Structure of Interest Rates. Journal of Finance, 29(2), 449–70.
33. Merton, R. (1977). An Analytic Derivation of the Cost of Loan Guarantees and Deposit Insurance: An Application of Modern Option Pricing Theory. Journal of Banking and Finance, 1(1), 3–11.
34. Merton, R. (1998). Applications of Option-Pricing Theory: TwentyFive Years Later. The American Economic Review, 88(3), 323–349.
35. Ogden, J. (1987). Determinants of the ratings and yields on corporate bonds: test of contingent claims model. The Journal of Financial Research, 10(4), 329-340.
36. Rodríguez, S. (2004). Aplicación del modelo de riesgo crediticio EDF para las empresas en Colombia. Tesis no publicada, Facultad de Ingeniería, Universidad de los Andes.
37. Tavakoli, J.M. (2001). Credit Derivatives and Synthetic Structures: A Guide to Instruments and Applications (2da ed.). New York, NY: John Wiley & Sons.
38. Teixeira, J.C. (2007). An empirical analysis of structural models of corporate debt pricing. Applied Financial Economic, 17(14), 1141-1165.
39. Vasicek, O. (1977). An equilibrium characterization of the term structure. Journal of Financial Economics, 5(2), 177-88.