CÓMO CREAR UN PORTAFOLIO DE INVERSIÓN CON LAS OPCIONES QUE OFRECEN LOS FONDOS DE PENSIONES VOLUNTARIAS EN COLOMBIA: EL CASO DE SKANDIA1
LUIS BERGGRUN PRECIADO*1, VIRGINIA CAMACHO ROGER2
1Ph.D. candidate in Finance, Tulane University, Estados Unidos. Profesor de tiempo completo, Universidad Icesi, Colombia. Miembro Grupo de Investigación “Inversión, Financiación y Control”, Universidad Icesi, Grupo Categoría B de Colciencias, Colombia. Dirigir correspondencia a: Universidad Icesi, Calle 18 No. 122-135, Cali, Colombia. lberggru@icesi.edu.co
2Profesional en Finanzas y Relaciones Internacionales, Universidad Externado de Colombia, Colombia. Financial Planner, InvesSka Agencia comercial Exclusiva de Skandia, Colombia. virroger@hotmail.com
* Autor para correspondencia.
Fecha de recepción: 16-04-2009 Fecha de corrección: 20-11-2009 Fecha de aceptación: 26-11-2009
RESUMEN
Este caso consiste en aplicar el modelo de construcción de portafolios de Markowitz (1952) para armar portafolios óptimos a partir de la mezcla de varias alternativas de inversión que ofrece un Fondo de Pensiones Voluntarias como Skandia, con diversas clases de riesgo, teniendo en cuenta el nivel de aversión al riesgo de los inversionistas.
PALABRAS CLAVE
Portafolios óptimos, línea de mercado de capitales, asignación de capital, nivel de aversión al riesgo, riesgo.
Clasificación JEL: C61; G11
ABSTRACT
How to develop an investment portfolio considering the different alternatives that voluntary pension funds offer in Colombia: the Case of Skandia
This case applies Markowitz methodology to find optimal portfolios built from different investment alternatives offered by Skandia’s Voluntary Pension Funds taking into account different types of risk and risk aversion attitudes of investors.
KEYWORDS
Optimal portfolios, capital market line, capital allocation, risk aversion level, risk.
RESUMO
Como criar um portafolio de investimento com as opções que oferecem os fundos de pensões volutarias em Colômbia: o caso de Skandia
Este caso consiste em aplicar o modelo de construção de portafolios de Markowitz para armar portafolios ótimos a partir da mistura de várias alternativas de investimento que oferece um Fundo de Pensões Voluntárias como Skandia, com diversas classes de risco, tendo em conta o nível de aversão ao risco dos inversionistas.
PALAVRAS-CHAVE
Portafolios ótimos, linha de mercado de capitais, asignación de capital, nível de aversão ao risco, risco.
INTRODUCCIÓN
La complejidad del mercado bursátil colombiano, los altos costos de transacción que aún manejan las firmas comisionistas de bolsa, sumado al poco conocimiento de las personas con capacidad de ahorro, que no son financistas, sobre la forma de negociar títulos valores, plantean enormes dificultades para acercar de manera informada y cómoda a los ahorradores e inversionistas colombianos a las oportunidades de inversión que ofrece el mercado de valores.
A partir de la Ley 100 de 1993, cuando se creó el Sistema General de Pensiones y el Régimen de Ahorro Individual con Solidaridad, y luego con el Estatuto Tributario (Art.126-1) que incentiva el ahorro a largo plazo (cinco años) con beneficios tributarios importantes para los inversionistas, se desarrollaron empresas llamadas Administradoras de Fondos de Pensiones, las cuales se ocupan tanto de las pensiones Obligatorias como de las Pensiones Voluntarias, tal como se definen las inversiones en esa legislación.
Los inversionistas buscan un lugar seguro y confiable donde poner a rentar su dinero, que no sea el típico producto bancario con altas comisiones. Sin embargo, muchas veces no entienden la naturaleza de largo plazo de la inversión que realizan a través de los fondos de pensiones, ni se han informado respecto a la composición de su portafolio para conocer qué lo puede afectar.
Es en la construcción de los portafolios, que vienen siendo el producto ofrecido por los fondos de pensiones, y los servicios de asesoría en planeación financiera, donde está la esencia del valor agregado que estos fondos ofrecen a sus clientes.
Es por esto que, con el fin de mejorar la comprensión de los usuarios actuales y potenciales de este mecanismo de inversión, se hace necesario estudiar cómo organiza y construye los portafolios de inversión una persona que tenga claros sus objetivos financieros en valor y en tiempo, asesorada por su Financial Planner.
Este caso tiene el objetivo de mejorar la comprensión de los ahorradores e inversionistas colombianos sobre el funcionamiento de los portafolios de inversión en Colombia y específicamente:
a. Aportar herramientas objetivas para que una persona pueda decidir dónde invertir su dinero y evaluar el desempeño de portafolios de inversión, de manera que pueda conocer con mejor criterio el mismo y tenga una idea de qué esperar en el futuro.
b. Realizar un marco teórico que explique cómo se construye un portafolio óptimo.
c. Explicar cómo se construyen portafolios óptimos basándose en las diferentes alternativas de inversión que ofrece Skandia, y en las diversas necesidades que tienen los clientes según sus características de aversión al riesgo.
d. Conocer cómo se construye un portafolio, comprender los factores que van a producir efectos (positivos y negativos) en el desempeño de los portafolios.
1. ADMINISTRACIÓN DE PORTAFOLIOS
Los inversionistas muestran comportamientos de personas adversas al riesgo. Estos inversionistas no soportan el riesgo a toda costa. Esto es, exigen un mayor retorno cuando el riesgo de su inversión es también mayor. La premisa básica del común de las personas es “no pongas todos los huevos en la misma canasta”. Lo anterior, en lenguaje técnico se considera diversificación. Sin embargo uno no diversifica a la ligera, repartiendo todo su dinero entre todas las opciones de inversión. Cada inversionista tiene gustos y límites presupuestales diferentes. Los criterios que se deben tener en cuenta al momento de construir un portafolio es de lo que trata esta sección.
2. CONSTRUCCIÓN DE PORTAFOLIOS
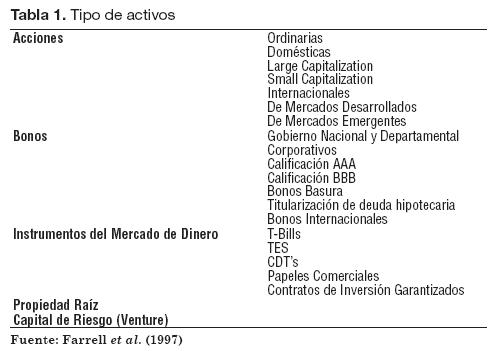
El proceso de construcción de portafolios se estructura en varias fases. La primera implica la definición de los tipos de activos elegibles. Estos generalmente se clasifican en acciones, bonos e instrumentos del mercado de dinero. Dentro de cada clase hay una cantidad sustancial de instrumentos financieros (Tabla 1).

La segunda fase es la creación de expectativas frente al rendimiento potencial y la determinación de la exposición al riesgo de cada activo financiero y de los tipos de activos. Esta fase es clave para la creación del portafolio y la valoración de los activos financieros y debe hacerse con extremo cuidado. Cuando se crea un portafolio en el que se tiene un título libre de riesgo combinado con un título que sí tiene riesgo, se puede crear la Línea de Activos de Capital (Capital Asset Line – CAL) que muestra todas las combinaciones de riesgo-rendimiento posibles dadas las diferentes opciones de porcentajes invertidos en cada tipo de activo. Su pendiente indica el retorno adicional por el mayor riesgo asumido.
La tercera fase es dónde se seleccionan los activos y la proporción de inversión en cada uno. Esta decisión implica definir la proporción invertida en activos riesgosos y activos no riesgosos y se conoce como Capital Allocation. Aquí es importante tener en cuenta no solo la relación riesgo-retorno de cada activo financiero individualmente sino también cómo interactúan a lo largo del tiempo (su covarianza).
2.1. Aplicación del proceso de construcción de portafolios
Fase 1. Tipos de activos elegibles
La Tabla 1 resume los distintos tipos de activos de los que se dispone en los mercados.
Para este caso se consideran las siguientes opciones de inversiones ofrecidas por Skandia a través de doce diferentes portafolios (Tabla 2).

Fase 2. Creación de expectativas frente al rendimiento potencial y la determinación de la exposición al riesgo de cada activo financiero y de los tipos de activos
El desarrollo matemático expresado a continuación se basa en los libros de Sharpe, Alexander y Bailey (1999) y Farrell, Reinhart y Farrell (1997); las fórmulas abajo anunciadas provienen de estas dos obras.
Si se parte de títulos de renta variable como las acciones, se comienza por calcular el rendimiento esperado de una acción individual.
El rendimiento esperado (Eri) de una acción se determina con base en varios escenarios posibles y la probabilidad de que se presenten esos escenarios, como se muestra en la Ecuación (1):
Donde:
Ps Probabilidad de que se presente el escenario s
Rs Rendimiento del título en el escenario s
Los rendimientos de una acción vienen dados por:
R= (Dividendo/ Precio0)+(Precio1- Precio0) / Precio0
La simple ponderación que se utilizó para calcular el retorno esperado no aplica para calcular el Riesgo de un portafolio compuesto por varias acciones. Este riesgo se calcula usando la desviación estándar del retorno. En el cálculo del riesgo del portafolio se tiene en cuenta también las correlaciones de los diferentes activos que componen el portafolio, haciendo que las ponderaciones sumen 1 por lo general.
Se parte del cálculo de los rendimientos de un título individual, tal como se mostró anteriormente.
En segundo lugar, se calcula la varianza del rendimiento de un título individual:
En tercer lugar, se calcula la desviación estándar del rendimiento del título, S:
Ahora se calcula la covarianza para saber cómo reacciona un título ante el movimiento de otro título:
Finalmente se calcula el coeficiente de correlación:
Este coeficiente de correlación siempre va a estar dentro de un rango desde -1 hasta +1, siendo -1 un indicador del movimiento completamente opuesto entre los títulos; +1 indica un movimiento en el mismo sentido; y un coeficiente de correlación en 0 indica que no existe relación alguna entre los movimientos de los rendimientos de los títulos.
La idea en la diversificación es tomar dos o más títulos con coeficiente de correlación inferior a +1 para disminuir el riesgo dentro de un portafolio (a menor correlación, menor riesgo total del portafolio). Al conformar el portafolio, se debe tener en cuenta el peso o proporción invertida en cada título, en lugar de su probabilidad de renta. El rendimiento esperado de un portafolio será:
Donde:
Er Rendimiento esperado del portafolio
Wi La proporción invertida en el título i
E(ri) Rendimiento esperado del título i
La varianza de los rendimientos de un portafolio no es sólo igual al promedio ponderado de la varianza de los rendimientos de los títulos que lo componen, porque hace falta tener en cuenta también la relación entre éstos, es decir, su covarianza. Luego, la varianza del rendimiento de un portafolio es:
Donde, W es el porcentaje invertido en cada título.
La varianza de un portafolio es el promedio ponderado de las varianzas de cada título más la covarianza entre cada título y los demás títulos del portafolio.
En este caso se utilizan datos históricos de cada portafolio desde septiembre 21 de 2004 hasta septiembre 27 de 2008, cuando recién empezaron las caídas de las bolsas con la quiebra de Lehman Brothers, asumiendo que el escenario más probable es que se repitan estas rentabilidades en situaciones más normales. A continuación, en la Tabla 3 se presentan los estadísticos referentes al promedio anual de las rentabilidades de los portafolios, así como su desviación estándar.
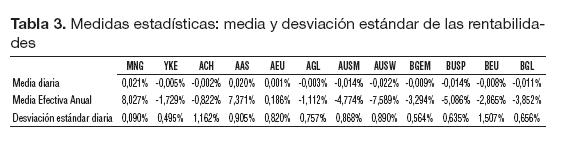
Se tienen varios fondos con rentabilidad esperada (Media) negativa. El que mayor rentabilidad arroja es el de AAS, y MNG es el que menos riesgo (desviación estándar) presenta. El fondo con mayor volatilidad es el de BEU, seguido por ACH.
En la Tabla 4 se muestran las covarianzas entre los fondos. Se destaca que la mayoría covarían en el mismo sentido salvo MNG-YKE; MNG- BGEM; MNG-BGL y MNGBUSP, los cuales covarían en sentido opuesto.

Fase 3. Teniendo en cuenta perfiles de riesgo
El modelo de construcción de portafolios de Markowitz (1952), indica que la meta debería ser generar un portafolio que ofrezca el más alto rendimiento con un nivel de riesgo definido. A esto se le llama un Portafolio Eficiente. El modelo de Markowitz ofrece un estricto proceso de construcción llamado Optimización, que ha sido utilizado para determinar la mejor mezcla de clases de activos más importantes para el portafolio, o Asset Allocation, por su traducción al ingles.
Se debe tener en cuenta el riesgo de cada activo a la hora de construir un portafolio, por el balance entre el riesgo y el retorno. Se puede continuar diversificando a más de dos acciones para disminuir la exposición a factores propios de cada empresa (riesgo único), haciendo que disminuya la volatilidad del portafolio. Pero existe un límite. No se puede suprimir por completo el riesgo dado que todas las acciones están expuestas a factores macroeconómicos comunes, el cual se suele medir por el coeficiente ß del modelo CAPM.
La proporción a invertir en cada portafolio Wi se define partiendo de la aversión al riesgo de cada individuo. La definición del nivel de aversión al riesgo, A, no es una actividad a tomar a la ligera. Tratándose de una variable subjetiva, existen diferentes tests que se realizan a los inversionistas al principio de su inversión para determinar lo mejor posible esta aversión. Uno de ellos se muestra en el Anexo 1.
Se pueden tomar como ejemplo tres personas de diferentes edades y distintos estilos de vida:
Teniendo en cuenta la edad y las etapas de la vida de las personas nombradas anteriormente, generalmente se cuantifica el intercambio retorno – riesgo y el nivel de aversión al riesgo a través de una función de utilidad. Uno puede definir un perfil de riesgo arriesgado para el joven (es decir, un nivel de aversión al riesgo “A” bajo: en el cual se cuantifica su aversión en A=1); moderado para la mujer (A=3) y conservador para el hombre próximo a retirarse (A=6).
Teniendo A, se puede determinar la función de utilidad (basada la relación riesgo-retorno de la inversión) que se debe maximizar:
Donde:
A es el coeficiente de la aversión al riesgo del inversionista (se mide entre 1 y 8, a mayor A, mayor aversión)
σ1 E s la desviación estándar de los retornos del portafolio
rƒ Es la tasa libre de riesgo
Luego Wi , como proporción a invertir en un portafolio arriesgado viene dada por:
1- Wi será la proporción invertida en el portafolio sin riesgo.
La construcción de un portafolio óptimo (en otras palabras, como a la vez se repartirá Wi ) tendrá en cuenta activos financieros con correlación inferior a +1, la aversión al riesgo del inversionista (A) y la razón de premio sobre volatilidad, que no es más que la pendiente de la línea CAL (Sp), la cual se debe maximizar:
Con ∑ Wi = 1
Además, al resolver este problema de optimización, se suele incluir la restricción que las ponderaciones de los activos en el portafolio riesgoso oscilen entre cero y uno.
Diversificar aún más el portafolio con activos internacionales puede ser benéfico para los re sultados del mismo dado que permite ingresar activos con un bajo nivel de correlación con los activos domésticos, lo que permite maximizar los rendimientos y mantener el nivel de riesgo deseado.
El tipo de cambio entre la moneda local y la extranjera entra a jugar un papel importante en la consecución de rendimientos. Su variación va a impactar los rendimientos generados por los activos internacionalmente, de ahí surge el riesgo cambiario que puede o no ser cubierto mediante operaciones de cobertura como forwards y opciones.
Sin embargo, se debe tener en cuenta una particularidad que describen Farrell et al., 1997:
Un estudio sobre la dinámica de las correlaciones entre los mercados de Asia–Pacífico, Europa y Estados Unidos (Hyde, Bredin y Nguyen, 2007) comprueba que las correlaciones entre los mercados incrementaron durante la caída de mercados entre el 2000 y 2003. Desde septiembre del 2008 se ha hecho evidente este contagio de crisis a nivel internacional en todos los mercados financieros.
3. COMENTARIOS FINALES
Conociendo la diversidad de portafolios accesibles en el mercado, una persona debe buscar opciones de inversión que se adapten a su perfil y que, dado ese perfil, obtenga el mejor rendimiento posible.
A continuación, en la sección de preguntas para discusión, se propone conformar portafolios óptimos para varios tipos de inversionistas, utilizando el programa MATLAB.
Como ejercicio, el lector debe comparar estos resultados con el estudio de la varianza y la covarianza y confirmar si los portafolios óptimos se componen en mayor medida por los portafolios con menor desviación estándar cuando la aversión al riesgo es mayor, y también establecer que a menor riesgo asumido, menor rendimiento obtenido. Pero la mayor conclusión debe ser la consecución de una mezcla de activos para el perfil de riesgo asignado que ofrezca una rentabilidad mejor con una volatilidad menor que una inversión en un solo activo.
4. PREGUNTAS PARA DISCUSIÓN
a. Efectúe un análisis de estadística descriptiva sobre estos rendimientos: Calcule la mediana, la media y la desviación estándar. ¿Qué portafolio tiene menor desviación estándar? ¿Qué portafolio tiene mayor volatilidad?
b. Calcule las covarianzas entre todos los portafolios. Describa cómo reaccionan los portafolios con respecto a movimientos de otros portafolios según los resultados de la matriz de varianza-covarianza.
c. Según la Tabla 5 de dominancia estocástica de segundo grado donde un “1” se interpreta como que el portafolio domina al portafolio en la columna y “0” si no hay dominancia, ¿cuál portafolio domina más veces y esto qué implica?
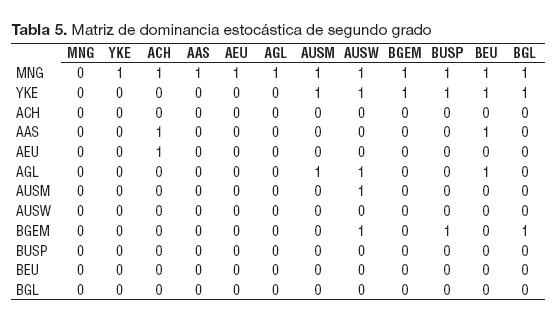
Según este criterio, el portafolio i dominará de manera estocástica al portafolio j si:
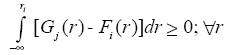
Donde G y F representan las distribuciones de probabilidad acumulada de los retornos de los portafolios j e i, respectivamente.
Esto significa que para que i domine a j, el área acumulada bajo la función de probabilidad acumulada de j debe ser mayor que el área acumulada para i; esto implica, a diferencia de la dominancia estocástica de primer orden, que las funciones de probabilidad acumulada se pueden cruzar. La dominancia estocástica de segundo orden se puede entender en el sentido en que entre dos activos con igual media, dominará aquel activo que tenga menor varianza.
Este criterio requiere que la diferencia de áreas para la función de densidad acumulada sea positiva bajo cualquier nivel dado de retorno r . La Tabla 5 muestra todas las duplas de portafolios posibles y los resultados del análisis de dominancia estocástica de segundo grado.
d. Utilizando el programa MATLAB r2008b y basándose en las rentabilidades diarias de los 12 fondos estudiados, construya la matriz de covarianzas y calcule varias mezclas de estos portafolios que se encuentren en la frontera eficiente (para ello revise el Finance MATLAB Userguide, en concreto, puede utilizar las funciones frontcon y portalloc).
e. Hacer el test de aversión al riesgo (Anexo 1) a 3 personas de edades diferentes y definir la variable de nivel de riesgo A (MATLAB solo permite ingresar valores para A entre A=1 y A=8). A mayor valor de A, más aversión al riesgo. La aversión al riesgo es una medida subjetiva, por esto se aplican test para medirla. Escoger tres niveles de aversión (=3 perfiles) diferentes para los siguientes pasos.
f. El siguiente paso es introducir el portafolio o activo libre de riesgo a manera de tasa libre de riesgo, la tasa de préstamo se asumirá que es la misma tasa libre de riesgo. Se escogió la tasa libre de riesgo con base en un fondo que tiene unos rendimientos muy similares a la DTF en Colombia (ver Tabla 6).

Aplicar fórmula de portafolio óptimo con los valores de nivel de riesgo para el primer perfil escogido, y con la tasa libre de riesgo. De esta manera obtendrá las participaciones relativas del portafolio riesgoso y el activo libre de riesgo sobre el portafolio total.
g. A continuación, con ese mismo perfil, aplique restricciones / límites definidos por usted (puede restringir la proporción invertida en algún tipo de activo o en alguna región, u otra restricción de acuerdo con el perfil estudiado). Cree un nuevo portafolio óptimo con esta restricción.
h. Repita el paso anterior para los otros dos perfiles.

NOTAS AL PIE PÁGINA
1. El caso corresponde al resumen de trabajo de grado preparado por Virginia Camacho Roger para obtener el título de Maestría en Administración en la Universidad Icesi, 2009. El trabajo de grado se realizó bajo la dirección del profesor Luis Berggrun. El caso es propiedad de la Universidad Icesi.
REFERENCIAS BIBLIOGRÁFICAS
1. Alexander, G.J., Sharpe, W.F. y Bailey, J.V. (2001). Fundamentals of investments (3ra ed.). Upper Saddle River, NJ: Prentice Hall.
2. Bruce, J. (2001). All about mutual funds (2da ed.). New York, NY: McGraw-Hill.
3. Elton, E. y Gruber, M. (1995). Modern Portfolio Theory and investment analysis (5a ed.). New York, NY: John Wiley and Sons.
4. Farrell, J.L., Reinhart, W.J. y Farrell, J.L. (1997). Portfolio management: theory and application (2da ed.). New York, NY: McGraw- Hill.
5. Grinold, R. y Kahn, R. (2000). Active Portfolio Management (2da ed.). New York, NY: McGraw- Hill.
6. Hyde, S.J., Bredin, D.P. y Nguyen, N. (2007). Correlation dynamics between Asia-Pacific, EU and US stock returns. Germany: University Library of Munich.
7. Markowitz, H. (1952). Portfolio Selection. Journal of Finance, 7(1), 77-91.
8. Murphy, J. (2003). Análisis Técnico de los Mercados Financieros. Barcelona: Gyersa.
9. O’Loughlin, J. (2005). The Real Warren Buffet: Managing Capital, Leading People. Clerkenwell, London: Nicholas Brealy Publishing.
10. Orléan, A. (2006). El poder de las Finanzas (1ra ed.). Bogotá, Colombia: Universidad Externado de Colombia.
11. Roberts, R. (2008). Wall Street - Mercados, mecanismos y participantes (1ra ed.). Buenos Aires: El Comercio S.A.
12. Ross, S., Westerfield, R. y Jaffe, J. (2005). Corporate Finance (7ma ed.). Singapore: McGraw- Hill.
13. Sharpe, W., Alexander, G. y Bailey, J. (1999). Investments (6a ed.). New Jersey, NJ: Prentice Hall.
14. Artículo 126-1, Estatuto Tributario colombiano. Disponible en: http://www.dian.gov.co/dian/15servicios.nsf/