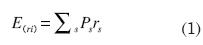
PROYECCIÓN DE LA TASA DE CAMBIO DE COLOMBIA BAJO CONDICIONES DE PPA: EVIDENCIA EMPÍRICA USANDO VAR¹,²

CATHERINE FAYAD HERNÁNDEZ¹, ROBERTO CARLOS FORTICH MESA*², IGNACIO VÉLEZ-PAREJA³

¹Profesional en Finanzas y Negocios Internacionales, Universidad Tecnológica de Bolívar, Colombia. Auxiliar de compras internacionales y nacionales, Propilco, Colombia. catherine.fayad@propilco.com

²Maestría en Economía, Universidad del Rosario, Colombia. Profesor de tiempo completo, Universidad Tecnológica de Bolívar, Colombia. Dirigir correspondencia a: Cra 21 No. 25-92, Universidad Tecnológica de Bolívar Sede Manga, Edificio MB, P. 4. Cartagena, Colombia rfortich@unitecnologica.edu.co

³Master of Science en Industrial Engineering, University of Missouri, Estados Unidos. Profesor Asociado, Universidad Tecnológica de Bolívar, Colombia. Grupo de investigación Instituto de Estudios para el Desarrollo, IDE, Colombia. ivelez@unitecnologica.edu.co

*Autor para correspondencia.

Fecha de recepción: 06-05-2009 Fecha de corrección: 12-11-2009 Fecha de aceptación: 26-11-2009

RESUMEN

El trabajo evalúa la proyección de la tasa de cambio (peso colombiano/dólar) con datos de 1995 a 2005 de Colombia a través del modelo de Tasa de Cambio de Paridad de Poder Adquisitivo (TCPPA). Se realizó una comparación del desempeño en la muestra (reservando los datos históricos de 2001 a 2005) de las proyecciones de modelos que utilizan la PPA, con las de un modelo de Vectores Autorregresivos (VAR). El método VAR tiene mejor desempeño para predecir la tasa de cambio nominal, de acuerdo con los indicadores RMSE, MAE y U-Theil, mientras que de acuerdo con el MAPE en el primer y segundo mes pronosticado, el VAR tiene peor desempeño que los modelos que utilizan PPA.

PALABRAS CLAVE

Tasa de cambio, modelo de series de tiempo, modelación financiera.

Clasificación JEL: F31, C22, G17

ABSTRACT

Forecasting foreign exchange rates in Colombia assuming PPP conditions: empirical evidence using VAR

This document examines exchange rate forecasts during the 1995-2005 period, using a Purchasing Power of Parity Exchange Rate Model (PPPER). Our first finding is that the computed forecasts seem to validate the use of this model under certain conditions given that it performs well in predicting the behavior of the nominal exchange rate. Our second finding included a comparative analysis of out-of-sample forecasts (saving historical data) between the PPP-based forecast models and the Vector Autoregressive (VAR) model. The VAR has a better forecasting performance based on the RMSE, MAE, and U-Theil indicators. MAPE results measured on the first and second month-ahead forecasts indicate that the VAR model performs more poorly than the PPP-based models.

KEYWORDS

Foreign exchange, time-series model, financial forecasting.

RESUMO

Previsão da taxa de câmbio na Colômbia sob condições de PPC: evidência empírica usando VAR

Esse documento avalia as previsões da taxa de câmbio (peso colombiano/ dólar) com dados de 1995 a 2005 da Colômbia, usando um Modelo de Taxa de Câmbio de Paridade de Poder de Compra (TCPPC). Foi realizada uma comparação do desempenho na amostragem (reservando os dados do histórico de 2001 a 2005) das previsões de modelos que usam PPC, com as de um modelo de Vectores Auto-regressivos (VAR). O método VAR tem melhor desempenho para prever a taxa de câmbio nominal, de acordo com os indicadores RMSE, MAE e U-Theil, enquanto que de acordo com o MAPE no primeiro e segundo mês prognosticados, o VAR apresenta pior desempenho que os modelos utilizando PPC.

PALAVRAS-CHAVE

Taxa de câmbio, modelo de séries de tempo, modelação financeira.

INTRODUCCIÓN

Un hecho empresarial que resulta importante es el de comprender cómo se proyecta la tasa de cambio. Esta es una variable que puede influir significativamente sobre la calidad de la toma de decisiones financieras y es indudable que la incertidumbre acerca del comportamiento de la tasa de cambio puede acarrear diferentes consecuencias negativas sobre las empresas. Por ejemplo, para los importadores una depreciación de la moneda aumenta sus costos de la producción, de los insumos, de las materias primas, entre otros. Los exportadores, a su vez, ven agravados sus problemas durante las apreciaciones de la tasa de cambio. Lo anterior es poco si se le añade el tema del pago de pasivos expresados en denominaciones extranjeras y otras decisiones relacionadas con el cubrimiento del riesgo cambiario de la empresa, los cuales pueden llegar a multiplicar la vulnerabilidad del negocio ante cambios súbitos de la tasa de cambio.

En la práctica, los empresarios no se preocupan por perfeccionar una metodología que les asegure buenas proyecciones de los indicadores de tasa de cambio, lo cual es preocupante si se tiene en cuenta que estas proyecciones tampoco se encuentran disponibles en ningún medio informativo oficial. ¿Qué es lo que se hace entonces? Lo más usual es que se use información histórica, ya sea para predecir el comportamiento futuro o para suponer que el comportamiento histórico se mantendrá hacia el futuro, y sobre esta base hacer los estimativos. Dado que no existe ningún método de pronóstico infalible, lo que hacen estos procedimientos es estimar un valor posible pero siempre sujeto a errores.

Precisamente, en este trabajo se discutirán teorías económicas que intentan poner orden a la hora de explicar las variaciones de la tasa de cambio, para finalmente contrastar el nivel de acierto al que se llega utilizando diferentes conjuntos de modelos estadísticos. La motivación, pues, ha sido la de aplicar a datos reales distintas aproximaciones o enfoques de proyección de tasa de cambio, con el fin de comparar su desempeño, utilizando para ello indicadores que evalúan el nivel de desvío o error al que se llega en cada caso. Los resultados de estas comparaciones podrán servir para que un empresario que se haya enfrentado a estos datos sepa con certeza cómo le hubiese ido al usar alguno de los métodos de proyección propuestos.

Es necesario delimitar bien el alcance del presente trabajo. No se intentará comprobar empíricamente si se cumple la teoría de la PPA; esa literatura acude al uso de pruebas de raíz unitarias y modelos de cointegración y se puede consultar en Taylor (2002). Tampoco se espera hallar resultados sistemáticos o demostraciones matemáticas que revelen las condiciones en las cuales un método de proyección es mejor que otro; de modo que los resultados tienen validez únicamente para el periodo analizado en el caso colombiano. No se conocen antecedentes de pronósticos similares para otros países, por lo que es imposible generalizar los resultados.

El trabajo está organizado de la siguiente forma: en la sección 1 se presenta la teoría de la PPA y se explica su relación con la proyección de la tasa de cambio. En la sección 2 se realiza la proyección de la tasa de cambio utilizando el método VAR. Finalmente, la sección 3 presenta las conclusiones.

1. VOLATILIDAD DE LA TASA DE CAMBIO Y MODELACIÓN FINANCIERA: ¿ES ÚTIL LA HIPÓTESIS DE PARIDAD DE PODER ADQUISITIVO (PPA) PARA PROYECTAR LA TASA DE CAMBIO?

En teoría, cuando una empresa tiene relaciones comerciales con empresas de otros países se establecen diferencias en cuanto a los precios y la moneda; no obstante, existe la “Ley de un solo precio” que afirma que cuando se miden en moneda común, las mercancías libremente negociadas deberían costar lo mismo en cualquier parte del mundo. Así, la tasa de conversión de moneda extranjera a moneda nacional se denomina tasa de cambio, que en este caso se refiere al peso colombiano/ dólar. De acuerdo con todo lo anterior se obtiene lo que se conoce como tasa de cambio de paridad de poder adquisitivo (TCPPA) -Ecuación 1-.

Donde:

P_COL Precio de la canasta de bienes de referencia en Colombia

P_USA Precio de la misma canasta de bienes en Estados Unidos

Esta misma relación se puede expresar también en términos de tasas de variación porcentual (Ecuación 2).

Donde:

ΔTCPPA Variación porcentual en la tasa de cambio de paridad de poder adquisitivo a lo largo de un año

i_COL Tasa de inflación de Colombia

i_USA Tasa de inflación de Estados Unidos

Por otro lado, la tasa de cambio real (TCR) (Ecuación 3), puede interpretarse como el cociente entre la Tasa Representativa del Mercado (TRM) y la TCPPA, ya que busca recoger el diferencial entre el valor de mercado de la moneda y su valor teórico. Nótese que si la TRM fuese igual a la TCPPA, la TCR debería ser igual a 1. A su vez, la TRM puede despejarse de esta relación, para obtener la Ecuación 4.

Debido a que su comportamiento es más predecible que el de la errática TRM, algunos analistas financieros suelen usar la TCPPA en su lugar. De este modo, ante la necesidad de proyectar estados financieros donde se tengan en cuenta los valores futuros de la TRM, es común que se tome simplemente la Ecuación 2 (la cual supone por construcción que se cumple la Ley de un solo precio). Desde ese punto de vista, la variación de la TRM puede interpretarse como una versión modificada de la variación de la TCPPA, la cual se multiplica por una función de la tasa de variación de la TCR (Ecuación 5).

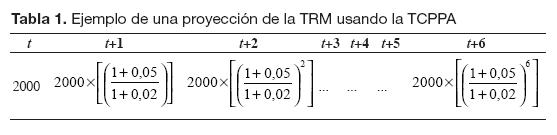
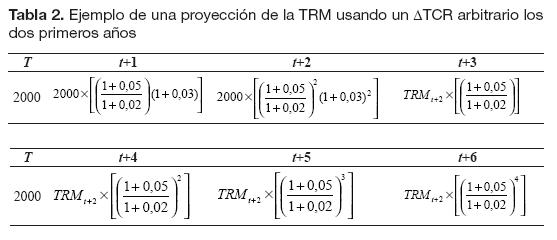
Otra práctica extendida en los departamentos financieros de las empresas, consiste en utilizar la Ecuación 5 en sus proyecciones, pero sólo durante los primeros años. Luego, se suele suponer que la Ecuación 2 es la que se verifica. Para ilustrar esto con un ejemplo, supóngase que se tiene la siguiente información: sea la TRM en t igual a 2000, y sean iCOL e iUSA iguales a 5% y 2%, respectivamente. Utilizando estos datos, es posible proyectar la TRM con dos métodos diferentes: en primer lugar puede utilizar la Ecuación 2 entre los periodos t+1 y t+6 (Tabla 1). En segundo lugar, podría suponerse arbitrariamente que los dos primeros años la tasa de variación de la TCR será de 3%, y que a partir de t+3 no presenta más variaciones (Tabla 2).

¿Qué tan válido resulta el uso de estos métodos para proyectar una TRM? Se trata de una cuestión empírica, la cual deberá ser juzgada en términos de su porcentaje de error respecto a los datos históricos, y respecto a su desempeño en comparación con otros métodos de pronóstico. En este trabajo se propone evaluar lo anterior con datos de la TRM de Colombia entre 1995 y 2005.

Desempeño del modelo TCPPA y el caso de información perfecta

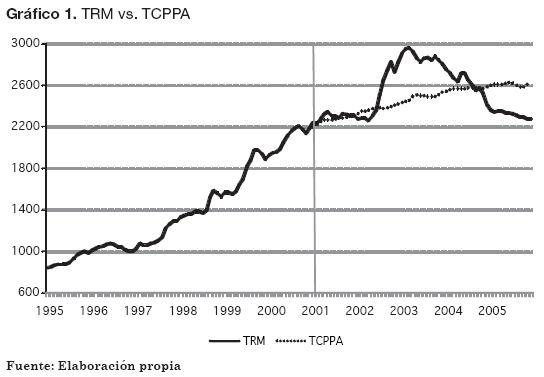
El modelo TCPPA con información perfecta corresponde a la proyección de la TRM durante el periodo de validación que se reservó para hacer los pronósticos, utilizando como datos de inflación doméstica y extranjera los valores históricos ocurridos durante tal periodo, y sirviéndose de la Ecuación 2 para realizar los cálculos. Los resultados de las proyecciones se muestran en el Gráfico 1. Esto equivale a suponer que el hipotético usuario o analista cuenta con una proyección perfecta de ambas inflaciones. En este punto debe aclararse el porqué es importante probar el modelo TCPPA con información perfecta: los resultados que se obtengan servirán de referencia ideal, y en cierta medida se pone a prueba el argumento de la PPA per se, despojándolo de cualquier ruido ocasionado por el uso de valores ficticios dentro de la Ecuación 2. Así, la prueba indicaría la bondad del método en sí mismo, y más adelante se realizará la misma prueba pero utilizando las inflaciones generadas mediante un VAR (a esto se le llamará TCPPA-VAR).

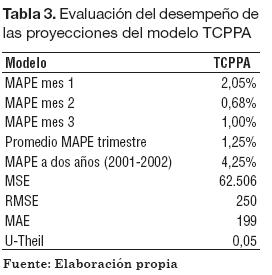
Para evaluar el desempeño de los pronósticos se utilizaron diferentes métodos, tales como el cálculo del error porcentual en el primero, segundo y tercer mes proyectados,³ y de otros indicadores estadísticos como el MSE, RMSE, MAE, y la U-Theil. La construcción de cada uno de estos indicadores puede consultarse junto con otros detalles metodológicos en De Gooijer y Hyndman (2006). Los resultados para el caso del modelo TCPPA (Tabla 3), indican que usar este método con los datos colombianos entre 2001 y 2005 hubiese significado un desfase de 2,05% para el primer mes pronosticado, y un 1,25% de error en promedio para el primer trimestre proyectado.

2. PROYECCIÓN DE LA TASA DE CAMBIO MEDIANTE VAR

Los datos utilizados en las proyecciones de la sección anterior se basaron en los valores históricos u observados de las inflaciones, así que no representan la información que verdaderamente tendrán a su disposición los usuarios o analistas interesados en estimar el comportamiento futuro de la TRM. Sin embargo, un ejercicio interesante que puede plantearse, es el de usar métodos estadísticos de series de tiempo para estimar las variables necesarias para poder calcular la TCPPA y la PPA-TCR. En este trabajo, se estimó un modelo VAR para conseguir los pronósticos de las variables TRM, TCR, i_COL e i_USA.

2.1. Descripción de los datos y metodología

Los métodos estadísticos de series de tiempo que se utilizaron requirieron de múltiples variables como insumo para su correspondiente estimación. En este trabajo las variables utilizadas se resumen en la Tabla 4.

Las variables utilizadas tuvieron una periodicidad mensual desde enero de 1995 hasta diciembre de 2005. Se consideró tomar estas variables macroeconómicas puesto que hacen parte de las cuentas de la balanza comercial informadas por el Banco de la República y su acceso es fácil para cualquier potencial usuario de los métodos que se proponen en este trabajo. A partir de las nueve variables elegidas, se hicieron pruebas de especificación de series de tiempo multivariadas para encontrar el número de variables óptimas a incluir en el modelo.

2.2. Especificación del modelo

El objetivo de utilizar una técnica de series de tiempo multivariada es poder contar con un método para proyectar la TCR y las inflaciones nacionales y, a su vez, incluir esos resultados en la Ecuación 5. El modelo de Vectores Autorregresivos (VAR) es una extensión multivariada de un modelo autorregresivo univariado. Todo VAR tiene dos dimensiones: la longitud u orden, p, que es igual al mayor de los rezagos incluido en la autorregresión; y el número, k, de las variables existentes modeladas conjuntamente. Para que un VAR esté correctamente especificado, el primer paso es elegir el número óptimo tanto de p como de k. Por ejemplo, un VAR de orden p en k variables se expresa como en la Ecuación 6.

Por otro lado, en la Ecuación 7 se expresa el mismo VAR(p) pero ahora en notación del operador de rezago multivariado, donde cada Π_i es una matriz de coeficientes de tamaño kxk. El segundo paso para una correcta especificación del VAR consiste en garantizar la propiedad de estacionariedad para que las técnicas de inferencia estándar puedan ser válidas.

La principal razón por la cual se eligió utilizar un VAR para realizar los pronósticos se debe a que su desempeño es superior al de los modelos de series de tiempo univariados lineales o ARIMA, los cuales son tradicionalmente utilizados para hacer proyecciones en economía. No obstante, según Patterson (2000) la metodología de VAR no está exenta de críticas: una de ellas es que existe un trade-off entre el número de variables que son incluidas en un VAR y el número de grados de libertad que quedan en la muestra. Al incluir más variables en el modelo se debe mejorar la especificación del mismo, pero ocurre que por cada variable añadida los grados de libertad de la estimación se reducen significativamente.

Un paso preliminar necesario antes de llevar a cabo las medidas de predicción para el modelo de tasa de cambio propuesto, es el de la determinación del orden de integración de los procesos generadores de los datos empleados en el análisis. Si las series fuesen no-estacionarias, esto acarrearía problemas debido a que no se podría estimar un proceso autorregresivo usando esos datos. Para lo anterior, inicialmente se analiza la estacionaridad de las series por medio de las prueba de Dickey–Fuller Aumentada o ADF por sus siglas en inglés.

2.3. Selección de orden y algoritmo de Dolado

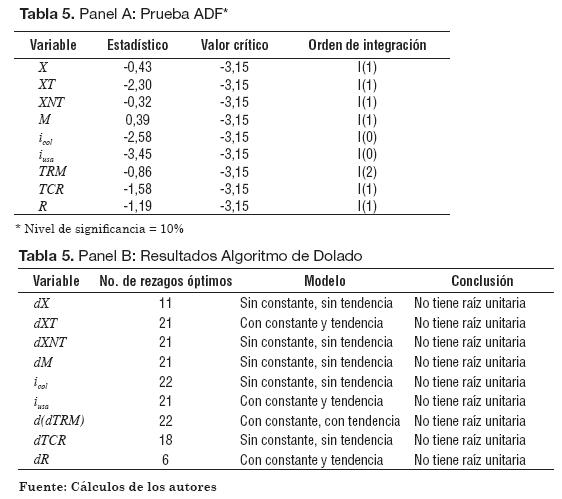
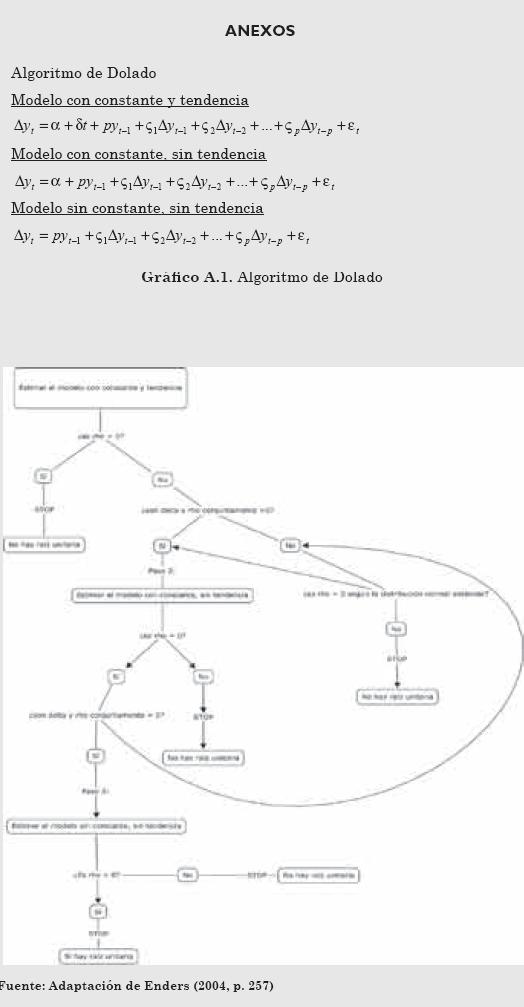
La prueba ADF se realizó estimando la ecuación para cada variable con rezago y con tendencia; el número de rezagos máximos incluidos en p se calculó con base en la recomendación de Hayashi (2000), y para evaluar la significancia del último rezago se utilizó la distribución normal al 10%.⁴ Si el rezago es estadísticamente diferente de cero, entonces los errores son ruido blanco; si no lo son, se reduce entonces el número de rezagos en 1 y se repite el proceso. De esta forma, se encontró el valor crítico y el estadístico para empezar el Algoritmo de Dolado y concluir si las variables tenían raíz unitaria o no, y el orden de integración para cada una de ellas al momento de incluirlas en el VAR.⁵ Los resultados se observan en la Tabla 5, Paneles A y B.

2.4. Estimación del modelo y procedimiento de pronóstico

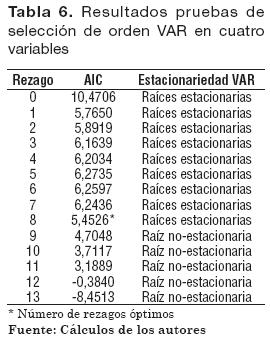
Se estimaron 245 ecuaciones VAR, resultantes de hacer todas las combinaciones posibles de variables y rezagos con las nueve variables disponibles. El siguiente paso en la especificación consistió en calcular para cada ecuación el valor del AIC (Akaike Information Criterion), en su versión tomada de Lütkepohl (1991), con el fin de utilizarlo como criterio de selección de orden. Luego, se hicieron pruebas de estacionariedad de las raíces sobre las ecuaciones seleccionadas para refinar la especificación del modelo, reduciendo así la búsqueda a 32 ecuaciones. La especificación final a la que se llegó fue un VAR(8) en cuatro variables: i_col, i_usa, d(dTRM) y dTCR. Los resultados del análisis se resumen en la Tabla 6.

Usando el VAR seleccionado se realizó un pronóstico dinámico. Se escogió una muestra de 11 años (132 meses), desde enero de 1995 hasta diciembre de 2005 y se dividió en dos submuestras. La primera es el periodo de estimación que abarca 72 meses, mientras que el periodo de validación consta de 60 meses; de esta forma se realizó una comparación de los datos obtenidos al aplicar el modelo con los verdaderamente ocurridos. Se analizó el desempeño de los pronósticos de la TRM utilizando los indicadores MSE, RMSE, MAE, MAPE y U-Theil.

2.5. Proyección directa de la TRM (TRM-VAR)

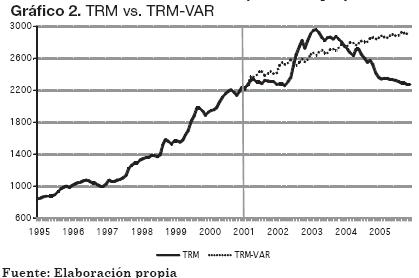
Se proyectó la TRM con el fin de compararla con el valor histórico (Gráfico 2). Puede observarse cómo la trayectoria creciente que tuvo la TRM antes de 2001 continúa representada en la TRM-VAR, al tener ésta pendiente positiva. El pronóstico parece ser consistente con los resultados que se obtienen en la literatura en relación con su desempeño (De Gooijer y Hyndman, 2006; Núñez, 2005; Patiño y Alonso, 2005), ya que solo son confiables en el corto plazo. Por otro lado, trabajar con datos de mayor frecuencia a la mensual pudo haber mejorado las proyecciones.

Para evaluar el desempeño de los pronósticos también se utilizaron diferentes métodos, tales como el MAPE en el primero, segundo y tercer mes proyectados, MSE, RMSE, MAE y la U-Theil. Los resultados para el caso del modelo TRM-VAR (Tabla 7) indican que usar este método con los datos colombianos entre 2001 y 2005 hubiese significado un desfase de 2,92% para el primer mes pronosticado, y un 1,41% de error en promedio para el primer trimestre proyectado.

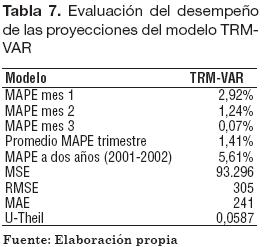
2.6. Desempeño del modelo TCPPA a partir de proyecciones del VAR

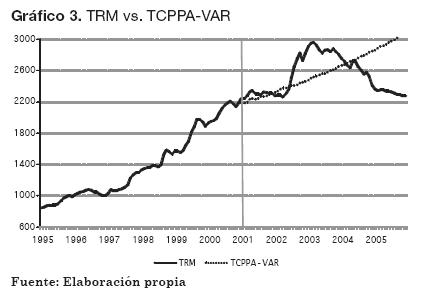
El modelo de TCPPA-VAR corresponde a la proyección de la TRM durante el periodo de validación que se reservó para hacer los pronósticos, utilizando como datos de inflación doméstica y extranjera los valores generados mediante el VAR, y sirviéndose de la Ecuación 2 para realizar los cálculos. Los resultados de las proyecciones se muestran en el Gráfico 3. En línea punteada se representa el valor proyectado de la TCPPA-VAR.

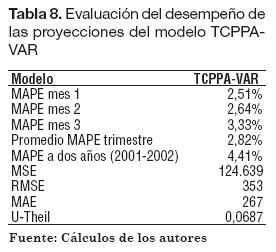
Al evaluar el desempeño de los pronósticos mediante el error porcentual en el primero, segundo y tercer meses proyectados, y demás indicadores estadísticos, se observa que se desfasó en un 2,51% para el primer mes pronosticado, y en un 2,82% de error en promedio para el primer trimestre proyectado (Tabla 8).

2.7. Desempeño del modelo PPA-TCR a partir de proyecciones del VAR

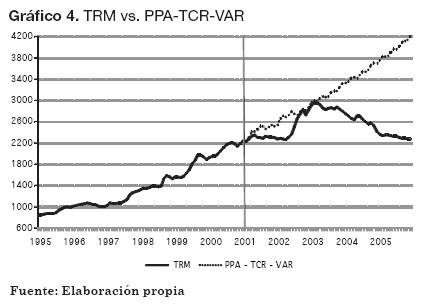
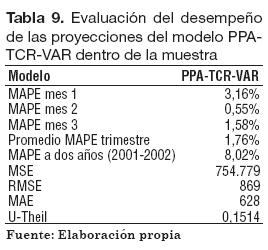
El desempeño del modelo PPA-TCRVAR puede verse en el Gráfico 4. En este modelo se utiliza la Ecuación 5 combinando simultáneamente los pronósticos de inflación de Colombia, inflación de Estados Unidos y TCR.

Para evaluar el desempeño de los pronósticos se utilizaron los diferentes métodos ya mencionados (MAPE en el primero, segundo y tercer meses proyectados, MSE, RMSE, MAE, y U-Theil). Los resultados para el caso del modelo TCPPA (Tabla 9) indican que usar este método con los datos colombianos entre 2001 y 2005 hubiese significado un desfase de 3,16% para el primer mes pronosticado, y un 1,76% de error en promedio para el primer trimestre proyectado.

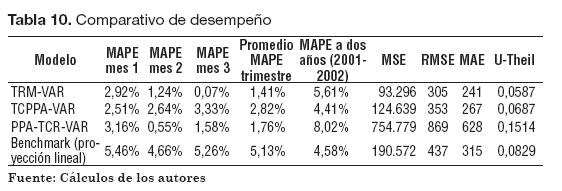
En este trabajo se hizo un ejercicio empírico de proyección de variables macroeconómicas, apoyado en la teoría de la Paridad de Poder Adquisitivo con el fin de explicar las variaciones de la tasa de cambio y verificar si ésta sirve para mejorar el nivel de acierto de las proyecciones. Para comparar el desempeño de las proyecciones, se incluyó también un modelo de series de tiempo multivariado y se aplicó principalmente a los datos de la TRM de Colombia entre 1995 y 2005. Un comparativo en el que se sintetizan los hallazgos se incluye en la Tabla 10.

¿Qué método debe usarse entonces para realizar la proyección de la TRM? Hay una propuesta que usa la llamada tasa de cambio de paridad de poder adquisitivo (TCPPA), cuyo uso frecuente por parte de las empresas fue la motivación de este artículo (Ecuación 2)

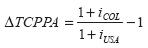
En realidad, la Ecuación 2 se usa con las mejores proyecciones que hay en el mercado de pronósticos, ya que no es posible conocer los valores futuros de las inflaciones domésticas y extranjeras. A su vez, las proyecciones de inflaciones que realizan los departamentos investigativos de entidades como Bancolombia, Corfinsura, Business Monitor International, etc., están por lo general basadas en métodos estadísticos sofisticados (e.g. Redes Neuronales Artificiales, métodos no-lineales, combinación de pronósticos, métodos de suavización exponencial, ARIMA, VAR). De este modo los resultados de las proyecciones con el modelo TCPPA-VAR equivalen a las que obtendría un empresario que adquiera en el mercado unas proyecciones de inflación, ya que el procedimiento de especificación del modelo VAR aquí usado fue similar al que rutinariamente hacen los equipos técnicos de entidades especializadas en comercializar proyecciones de series económicas.

Nótese que las proyecciones realizadas, aunque rescatables en el corto plazo, presentan un creciente margen de error que se traduce en que no sean confiables a la hora de necesitarse pronósticos de más largo plazo (superiores a los tres periodos futuros). Este resultado es consistente con lo observado en la literatura de proyecciones económicas basadas en métodos extrapolativos, a diferencia de lo que ocurre con otro tipo de variables (e.g. eventos astronómicos) que presentan unas características naturales que permiten prolongar la temporalidad del pronóstico.

La TCPPA, en el caso de información perfecta, produce un desfase de 1,25% en el pronóstico de corto plazo del modelo TCPPA, lo cual representa un error de sólo $25 respecto a una TRM de $2.000. En el largo plazo, este modelo pierde desempeño. El modelo TCPPA-VAR tiene un desempeño aceptable, como lo indica su U-Theil de 0,0687, superior al proporcionado por TRM-VAR, o al del benchmark (proyección lineal).⁶

3. CONCLUSIONES

De acuerdo con los resultados, un empresario que se enfrentara a los datos de la TRM hasta el año 2000, hubiese obtenido los mejores resultados en su proyección hacia 2001-2002 si utilizaba el modelo TCPPA-VAR, como lo muestra el MAPE a dos años. Sin embargo, el modelo VAR (TRM-VAR) arrojó los mejores resultados de acuerdo con los indicadores de evaluación MSE, RMSE, MAE y U-Theil. Esta discrepancia en el desempeño medido por diferentes indicadores se debe a que, mientras que unos utilizan toda la información de los cinco años proyectados, los MAPE se refieren únicamente a los tres primeros meses y a los dos primeros años. Por otro lado, se destaca que para proyecciones de largo plazo de la TRM, el modelo PPA-TCR-VAR tuvo los peores resultados en las evaluaciones de pronósticos. Para tener una idea de la magnitud del desvío, el desfase de 8,02% en el error promedio a dos años, respecto a una TRM de $2.000, significa desviarse en $160,4 del valor correcto.

Para futuras investigaciones, se recomienda replicar este ejercicio para otros países utilizando sus correspondientes tasas de cambio reales, con el fin de observar si los resultados son consistentes con lo aquí encontrado. Adicionalmente, dado que la tasa de cambio peso colombiano/dólar está disponible en periodicidad diaria, es posible calcular una proyección usando esa frecuencia, ante lo que se esperaría mejore el desempeño de todos los modelos. Finalmente, ya que el periodo de validación de las proyecciones fue de cinco años (45% de la muestra), se espera que al hacer el ejercicio con diferentes periodos de validación (e.g. 20% de la muestra) también podría alterar las conclusiones.

NOTAS AL PIE DE PÁGINA

1. Este documento fue seleccionado en la convocatoria para enviar artículos, Call for Papers, realizada en el marco del Simposio “Análisis y propuestas creativas ante los retos del nuevo entorno empresarial”, organizado en celebración a los 30 años de la Facultad de Ciencias Administrativas y Económicas de la Universidad Icesi y de los 25 años de su revista académica, Estudios Gerenciales; el 15 y 16 de octubre de 2009, en la ciudad de Cali (Colombia). El documento fue presentado en las sesiones simultáneas del área de “Finanzas”, el título de la presentación fue “Proyección de la tasa de cambio de Colombia bajo condiciones de PPA: evidencia empírica y demostración econométrica mediante VAR”

2. Se agradece a Gustavo López y David A. Londoño por su valiosa colaboración durante el desarrollo de una versión previa del trabajo. También se agradecen los comentarios de Jesús Otero para las pruebas de raíz unitaria.

3. El error porcentual medio se conoce como MAPE por sus siglas en inglés, mean absolute percentage error.

4. Procedimiento sugerido en Franses (1998), otros autores utilizan otros niveles de significancia; en este artículo los cálculos se hicieron al 10%.

5. La versión utilizada del Algoritmo de Dolado ha sido incluido en el Anexo A.

6. La proyección lineal es simplemente el resultado de la función Pronóstico incorporada en EXCEL.

REFERENCIAS BIBLIOGRÁFICAS

1. De Gooijer, J. y Hyndman, R. (2006). 25 years of time series forecasting. International journal of forecasting, 22(3), 443-473.

2. Enders, W. (2004). Applied econometrics time series. Hoboken, NJ: Wiley.

3. Hayashi, F. (2000). Econometrics. Princeton, NJ: Princeton University Press.

4. Lütkepohl, H. (1991). Introduction to multiple time series analysis. Berlín: Springer-Verlag.

5. Núñez, H. (2005). Una evaluación de los pronósticos de inflación en Colombia bajo el esquema de inflación objetivo. Revista de Economía del Rosario, 8(2), 151-185.

6. Patiño, C. y Alonso, J. (2005). Determinantes de la tasa de cambio nominal en Colombia: evaluación de pronósticos. Universidad ICESI (Mimeo). Disponible en: http://www.icesi.edu.co/~jcalonso/Contact/tcn2005.pdf

7. Patterson, K. (2000). An Introduction to Applied Econometrics: a Time Series approach. Basingtoke, UK: Palgrave McMillan.

8. Taylor, A. (2002). A century of Purchasing Power Parity. Review of economics and statistics, 84(1), 139-150.