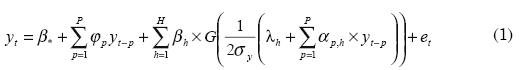
UN MODELO NO LINEAL PARA LA PREDICCIÓN DE LA DEMANDA MENSUAL DE ELECTRICIDAD EN COLOMBIA*
JUAN DAVID VELÁSQUEZ**1, CARLOS JAIME FRANCO2, HERNÁN ALONSO GARCÍA3
1Doctor en Ingeniería-Sistemas Energéticos, Universidad Nacional de Colombia, sede Medellín, Colombia. Profesor asociado, Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia, Colombia. Director, Grupo de Computación Aplicada, Facultad de Minas, Universidad Nacional de Colombia, Colombia. Dirigir correspondencia a: Cra 80 No. 65-223, Bloque M8A, Of. 206, Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. jdvelasq@unal.edu.co
2Doctor en Ingeniería-Recursos Hidráulicos, Universidad Nacional de Colombia, sede Medellín, Colombia. Profesor asociado, Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia, Colombia. Director, Grupo de Estudios de Energía, Facultad de Minas, Universidad Nacional de Colombia, Colombia. Dirigir correspondencia a: Cra 80 No. 65-223, Bloque M8A, Of. 210, Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. cjfranco@unal.edu.co
3Estudiante, Ingeniería de Sistemas, Universidad Nacional de Colombia, sede Medellín, Colombia. Miembro, Grupo de Estudios de Energía y Grupo de Computación Aplicada, Facultad de Minas, Universidad Nacional de Colombia, Colombia. Dirigir correspondencia a: Cra 80 65-223, Bloque M8A, Of. 201, Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. hagarciag@unalmed.edu.co
* Es producto de la investigación realizada por los grupos de Mercados de Energía y Computación Aplicada en el modelado y la predicción de variables económicas en mercados de electricidad. Patrocinado por la Facultad de Minas, Universidad Nacional de Colombia.
** Autor para correspondencia
Fecha de recepción: 15-10-2008 Fecha de corrección: 24-02-2009 Fecha de aceptación: 27-07-2009
RESUMEN
En este artículo se compara el desempeño de un modelo ARIMA, un perceptron multicapa y una red neuronal autorregresiva para pronosticar la demanda mensual de electricidad en Colombia para el siguiente mes adelante. Los datos disponibles fueron divididos en dos conjuntos, el primero para estimar los parámetros del modelo y el segundo para la capacidad de predicción por fuera de la muestra de calibración. Los resultados revelan que la red neuronal autorregresiva es capaz de pronosticar la demanda con mayor precisión que los otros dos modelos cuando la totalidad de los datos es considerada.
PALABRAS CLAVE
Demanda, pronóstico, redes neuronales, ARIMA.
Clasificación JEL: C450, C530
ABSTRACT
A non-linear model for forecasting the monthly demand for electricity in Colombia
This article provides a comparison of the performance of an ARIMA model, a multilayer perceptron, and an autoregressive neural network for forecasting the monthly demand for electricity in Colombia for the following month. The available data were divided into two different sets, i.e. one set for estimating the model parameters, and the other for evaluating the forecast ability outside the range of the sample calibration data. The results show that the autoregressive neural network is able to forecast the demand more accurately than the other two models when the total available data are considered.
KEYWORDS
Demand, forecast, neural networks, ARIMA.
RESUMO
Um modelo não linear para a previsão da necessidade mensal de eletricidade na Colômbia
Nesse artigo se compara o desempenho de um modelo ARIMA, um perceptrão multi-camada e uma rede neural autorregressiva para prever a necessidade mensal de eletricidade na Colômbia para o mês seguinte. Os dados disponíveis foram divididos em dois grupos, o primeiro para estimar os parâmetros do modelo e o segundo para a capacidade de previsão por fora da mostra de calibração. Os resultados mostram que a rede neural autorregresiva é capaz de prever a procura com maior precisão que os outros dois modelos considerados, quando a totalidade dos dados é considerada.
PALAVRAS-CHAVE
Procura, previsão, redes neurais, ARIMA.
INTRODUCCIÓN
La demanda de electricidad, junto con la oferta y la regulación, conforman las tres fuerzas fundamentales que gobiernan la evolución de los mercados de electricidad. Es bien sabido que el comportamiento de la demanda es el fruto de la interacción de un gran número de factores complejos que son propios de los mercados eléctricos (Franco, Velásquez y Olaya, 2008). La demanda es uno de los factores determinantes de los precios de la electricidad en los mercados eléctricos liberalizados, junto con las complejidades y el comportamiento del sistema de generación de electricidad y las reglas de mercado impuestas por la regulación. La evolución de la demanda está estrechamente relacionada con la evolución de los diferentes sectores económicos de la sociedad, los avances tecnológicos encaminados al uso más eficiente y racional de la energía y la estacionalidad del clima que puede variar los comportamientos típicos de estación a estación.
La predicción de la demanda es un insumo fundamental para los procesos decisorios operativos y estratégicos que realizan los agentes del mercado, pero resulta ser una tarea difícil debido a la cantidad y complejidad de los factores que influyen en su comportamiento. Desde un punto de vista institucional, la predicción de corto plazo es utilizada para planificar la operación del sistema, mientras que la predicción de largo plazo es usada habitualmente como un insumo en las decisiones de expansión en capacidad de generación y del sistema de distribución (Al-Saba y El-Amin, 1999).
Dada su importancia, no es sorprendente que se hayan dedicado muchos esfuerzos para comprender mejor cómo evoluciona la demanda, qué factores influyen en su comportamiento y en qué forma y qué modelos podrían ser más adecuados para estudiar su evolución histórica y para realizar predicciones. Entre los modelos más usados se encuentran: regresión multivariada, cointegración (Beenstock, Goldin y Nabot, 1999; Nasr, Badr y Joun, 2003), funciones de transferencia (Harris y Liu, 1993; Tserkezos, 1992) y modelos ARIMA (Barrientos, Olaya y González, 2007; Castaño, 2008; Murillo, Trejos y Carvajal, 2003); estos estudios han demostrado que, en general, la demanda depende principalmente de la temperatura (Abdel-Aal, Al-Garni y Al-Nassar, 1997; Harris y Liu, 1993; Mirasgedis, Sarafidis, Georgopoulou, Lalas, Moschovits, Karagiannis y Papakonstantinou, 2006; Tserkezos, 1992), el tamaño de la población (Al-Saba y El-Amin, 1999; Egelioglu, Mohamad y Guven, 2001), el crecimiento económico (ingreso per cápita o el producto interno bruto) (Medina y García, 2005; Nasr, Badr y Dibeh, 2000; Tserkezos, 1992) y el precio de la electricidad (Abdel-Aal y Al-Garni, 1997; Medina y García, 2005).
La predicción es hecha para diferentes escalas de tiempo según las necesidades particulares del agente; así, la predicción ha sido realizada para datos anuales (Ediger y Tatlidil, 2002; Egelioglu et al., 2001; Mohamed y Bodger, 2005), trimestrales (Beenstock et al., 1999; Tserkezos, 1992), mensuales (Abdel-Aal et al., 1997; Benavente, Galetovic, Sanhueza y Serra, 2005; Chaveza, Bernata y Coallab, 1999; Harris y Liu, 1993; Medina y García, 2005; Mirasgedis et al., 2006; Saab, Badr y Nasr, 2001),
diarios (Mirasgedis et al., 2006) e incluso para cada hora del día (Barrientos et al., 2007; Castaño, 2008; Murillo et al., 2003). Es sabido que para diferentes niveles de agregación temporal, una misma serie puede exhibir complejidades particulares que dificultan el desarrollo de un modelo; este es el caso general de las series de demanda que presentan, entre otras, fuertes patrones cíclicos de periodicidad anual, mensual, semanal, diaria y horaria, eventos atípicos como la presencia de días festivos, así como otras complejidades adicionales. Recientemente, Benavente et al. (2005) desarrollaron un método de paneles dinámicos con datos mensuales y procesos de ajuste no instantáneos y estimaron la elasticidad demanda residencial-precio. Igualmente, algunos estudios han demostrado que la respuesta de la demanda ante variaciones en sus determinantes puede ser no lineal.
El estudio de técnicas univariadas para el modelado y predicción de las series de demanda, está motivado en la necesidad de evitar la inclusión de variables explicativas y los correspondientes supuestos sobre su evolución, lo que aumenta la incertidumbre de los pronósticos. De esta forma, con los métodos univariados, las predicciones se hacen a partir de la dinámica propia de la demanda y pueden ser más precisas que las predicciones de los modelos explicativos (Abdel-Aal y Al-Garni, 1997). Una limitación de mucha técnicas univariadas es que los modelos obtenidos usan parámetros constantes en el tiempo, mientras que en la realidad ellos deberían cambiar para reflejar la evolución propia de los sistemas económicos. Sin embargo, no hay evidencias concluyentes de que alguna técnica de predicción sea superior a las otras (Nasr et al., 2003) y, desde un criterio puramente estadístico, aquellos modelos con menor error son de mayor interés (Chaveza et al., 1999).
En el caso colombiano, la proyección oficial de demanda es realizada por la Unidad de Planeación Minero-Energética del Ministerio de Minas y Energía (UPME) con una resolución anual de modelos econométricos que la relacionan con variables como el Producto Interno Bruto (PIB), las tarifas de energía y el crecimiento de la población (UPME, 2004). La proyección se hace usando diferentes escenarios para la evolución del PIB y las pérdidas en el sistema de transmisión. Posteriormente, las demandas proyectadas anuales son desagregadas a nivel mensual usando modelos ARIMA y pronóstico condicional. Estas proyecciones son consideradas como señales del mercado que deben ser interpretadas por los diferentes agentes dentro de sus procesos de toma de decisiones. Dichos modelos no están disponibles a los usuarios, de tal forma que ellos no pueden construir sus propios escenarios de proyección de la demanda.
Medina y García (2005) postulan que, adicionalmente a los factores considerados por la UPME, la demanda también depende del consumo de ACPM, de la presencia de fenómenos climáticos extremos y del consumo de gas natural. En dicho estudio, Medina y García comparan una red neuronal difusa y un perceptron multicapa al pronosticar la demanda mensual entre 1999:1 y 2004:11, considerando como entradas las variables descritas anteriormente. Esta aproximación reviste el problema de tener que conocer el valor futuro de las variables explicativas para poder efectuar la predicción de la demanda.
Barrientos et al. (2007) realizaron la predicción de la demanda a escalas horaria, diaria y mensual para la región suroccidental del país, usando funciones spline y modelos ARIMA. En este trabajo se desarrolló un modelo para cada hora del día para el periodo comprendido entre 2001:1 y 2001:12. Igualmente, Murillo et al. (2003) construyeron un modelo de la demanda de una empresa colombiana en el año 2001 usando la metodología ARIMA. Castaño (2008) desarrolló un modelo ARIMA con intervenciones, el cual fue usado para representar la dinámica de la demanda de la hora 12 en el periodo comprendido entre 1996:1 y 2002:8. Finalmente, Franco et al. (2008) modelaron la demanda mensual de electricidad para el periodo comprendido entre 1995:8 y 2006:1 usando un modelo de componentes no observables; la aproximación empleada por Franco et al. permitió separar la componente estacionaria asociada al ciclo anual de la tendencia de largo plazo; los autores concluyeron que la componente periódica posee un comportamiento estocástico de amplitud constante y que su tendencia revela una componente determinística lineal de crecimiento aproximadamente constante durante los últimos años, cuyas fases de crecimiento y decrecimiento coinciden con los ciclos del producto interno bruto.
El objetivo principal de este artículo es comparar la capacidad de un modelo ARIMA, un perceptron multicapa (MLP, por sus siglas en inglés) y una red neuronal autorregresiva (ARNN, por sus siglas en inglés) para pronosticar la demanda mensual de electricidad en Colombia usando únicamente datos de la demanda de los meses pasados.
La originalidad, relevancia e importancia de la investigación propuesta está basada en los siguientes aspectos:
En su orden se describe la información y metodología utilizada (Sección 1), los resultados obtenidos (Sección 2) y las principales conclusiones obtenidas (Sección 3).
1. INFORMACIÓN Y METODOLOGÍA
1.1. Información utilizada
Los datos con que se elaboró este estudio corresponden a la demanda total de electricidad del sistema interconectado colombiano, en miles de GWh mensuales, entre 1995:8 y 2008:6, los cuales están disponibles en el sistema Neón1 y recogen las características históricas desde la creación del mercado mayorista de electricidad.
Franco et al. (2008) encontraron que la serie presenta un patrón estacional determinístico de periodo anual y una tendencia estocástica de largo plazo; su tendencia reciente indica que existe un crecimiento sostenido desde el año 2000 hasta la fecha. La tendencia subyacente de largo plazo está relacionada con el crecimiento porcentual del producto interno bruto.
1.2. Metodología empleada
Las redes neuronales artificiales son modelos matemáticos que emulan, a un nivel muy simplificado, el procesamiento de información realizado por el cerebro. En términos estadísticos, ellas pueden ser entendidas como modelos no lineales de regresión (Sarle, 1994) que pueden aproximar cualquier función continua definida en un dominio compacto (Cybenko, 1989; Funahashi, 1989; Hornik, Stinchcombe y White, 1989). La revisión del estado del arte realizada por Zhang, Patuwo y Hu (1998) demuestra que estos modelos han sido ampliamente usados en la predicción de series de tiempo. Una de las falencias más importantes en este tópico es que no existe una metodología que sea aceptada de forma generalizada por la comunidad científica, sino más bien un grupo de pasos críticos que son adaptados a partir de heurísticas generales, la experticia propia del pronosticador y el conocimiento particular que se tenga de la serie analizada. Estos aspectos son discutidos en detalle por Kaastra y Boyd (1996) y Masters (1993, 1995). Una discusión más general sobre la problemática vigente en la predicción con modelos no lineales es presentada por Clements, Franses y Swanson (2004). Existe un volumen importante de experiencias reportadas que señalan la efectividad de los modelos de redes neuronales para el pronóstico de series de tiempo, entre los que se incluyen Conejo, Contreras, Espínola y Plazas (2005), Ghiassi, Saidane y Zimbra (2005), Heravi, Osborn y Birchenhall (2004), Swanson y White (1997a, 1997b) y Teräsvirta, Van Dijk y Medeiros (2005).
En este trabajo se emplea un modelo conocido como red neuronal autorregresiva (ARNN), cuyo uso ha sido poco difundido, y el cual está compuesto por un modelo lineal autorregresivo más un perceptron multicapa con una única capa oculta (Lee, White y Granger, 1993; Teräsvirta, Lin y Granger, 1993; White, 1989). En un modelo ARNN, la variable dependiente yt (que en este caso corresponde a la demanda) es obtenida después como una función no lineal de sus valores pasados yt-p como en la Ecuación 1; en donde ei son los residuales del modelo y para los cuales ei = σet , σ es la desviación estándar de los errores, et es una variable aleatoria que sigue una distribución normal estándar, β es un término constante que representa el peso de la conexión entre una neurona adaptativa y la neurona de salida, φp son los coeficientes de la componente autorregresiva del modelo, βh son los parámetros asociados a las conexiones de la capa oculta hacia la neurona de salida, λh son los parámetros asociados a las conexiones de la neurona adaptativa hacia las neuronas de la capa oculta, αp,h es la conexión de la neurona de entrada p hacia la neurona oculta h, G (.) es la función de activación de las neuronas de la capa oculta, H es el número de neuronas en la capa oculta, y es la desviación estándar de yt y su uso evita tener que transformar y para restringir sus valores al rango de la función G (.).
La función de activación de las neuronas de la capa oculta G(u) se define como en la ecuación 2, la cual se conoce como función sigmoidea bipolar. En la literatura más relevante se ha sugerido que funciones simétricas alrededor del origen, tal como (2), convergen más rápidamente que la función sigmoidea tradicional. Adicionalmente, la adición del término lineal 0,025u ayuda a la convergencia, ya que se evita la saturación de la neurona o unidad de procesamiento en la capa oculta y garantiza un gradiente mínimo cuando la salida neta de la función de activación sea cercana a sus valores extremos. Esto beneficia el proceso de optimización numérica, ya que evita que el algoritmo caiga en regiones planas donde el gradiente es prácticamente cero.
Los parámetros del modelo

La ecuación (2) es obtenida al suponer que los residuales et siguen una distribución normal con media cero y varianza desconocida. Es bien sabido que el modelo definido en (1) posee múltiples configuraciones que dan el mismo resultado para una entrada determinada. Dichas configuraciones son obtenidas al permutar las neuronas de la capa oculta, de tal forma que las conexiones que entran y salen de ellas son arrastradas al realizar la permutación. Esto es, las neuronas de la capa oculta intercambian su posición generando modelos diferentes cuyo comportamiento es idéntico.
Igualmente, se sabe que en algunos casos existe duplicidad de modelos. Esto se da para algunas especificaciones de G(.) para las cuales la contribución que llega de cada neurona oculta a la salida, permanece constante si los pesos de las conexiones que entran y salen de dicha unidad oculta son multiplicados por -1. Esto genera juegos de pesos que difieren en el signo, o sea, diferentes redes neuronales de comportamiento idéntico. Se ha argumentado que es adecuado imponer restricciones a los parámetros del modelo tal que se eviten los problemas mencionados; no obstante, no hay evidencias contundentes que indiquen que esta práctica permita obtener mejores modelos de redes neuronales. Por esta razón, no se impuso ningún tipo de restricciones para la estimación de los modelos.
A partir del modelo definido por (1) es posible obtener un modelo autorregresivo de orden P si se obliga a que H = 0. Igualmente, si se impone la restricción de que los parámetros φp sean cero con H > 0 , el modelo (1) equivale a un perceptron multicapa, ya que esto representa eliminar el modelo autorregresivo.
Lee et al. (1993), Teräsvirta et al. (1993) y White (1989) desarrollaron procesos de especificación para modelos ARNN a partir del uso de contrastes estadísticos. Este procedimiento permite seleccionar la cantidad H de neuronas de la capa oculta, así como los rezagos de la serie yt que deben incluirse en el modelo. Sin embargo, el objetivo fundamental de esta investigación es conseguir el mejor pronóstico posible y, ya que el procedimiento estadístico de especificación no garantiza esto, es necesario realizar una búsqueda exhaustiva entre los modelos posibles.
2. RESULTADOS OBTENIDOS Y DISCUSIÓN
En esta sección se presentan los resultados obtenidos al pronosticar el logaritmo natural de la demanda mensual de electricidad en miles de GWh para el periodo comprendido entre 1995:8 y 2008:6 usando un modelo ARIMA, un perceptron multicapa y una red neuronal autorregresiva. La serie consta de 155 datos; los primeros 131 (entre 1995:8 y 2006:6) fueron usados para estimar los parámetros de los modelos; los 24 restantes se usaron para evaluar su capacidad de predicción. Con el fin de analizar la influencia del horizonte de predicción sobre los resultados obtenidos, se consideraron horizontes de 12 (entre 2006:7 y 2007:6) y 24 (entre 2006:7 y 2008:6) meses, respectivamente.
Debido a que la serie estudiada presenta una clara componente de tendencia y un ciclo de periodicidad anual (Franco et al., 2008), se aplicó una diferenciación simple y una diferenciación estacional de periodo 12 al logaritmo de la demanda de electricidad. De esta forma, los parámetros de los modelos y los estadísticos de ajuste fueron obtenidos para la serie wt que fue obtenida como:
Donde dt es la serie de demanda mensual en miles de GWh, B es el operador de diferenciación, por definición Byt = yt-1; en consecuencia, B12yt = yt-12 (Box y Jenkins, 1976).
La popularización de los operadores de diferenciación utilizados es debida a que son una parte fundamental de la estrategia de especificación de los modelos SARIMA (Box y Jenkins, 1976), para los cuales se exige que la serie modelada sea estacionaria. Su fundamento teórico está basado en los conceptos de procesos con raíces unitarias y raíces estacionales. Estos conceptos se derivan de la condición de linealidad de la serie y no existen equivalentes teóricos para el caso de los modelos no lineales, tales como las redes neuronales; consecuentemente, su aplicación no está justificada desde la teoría.
No obstante, Masters (1993) recomienda el uso de los operadores de diferenciación en la predicción de redes neuronales ya que se eliminan características fácilmente identificables de la serie (la tendencia y el patrón estacional) y así, la red neuronal artificial puede concentrarse en aprender relaciones más sutiles y que son difícilmente identificables en los datos. Zhang y Qi (2005) presentan evidencia empírica para indicar que la sugerencia de Masters (1993) permite obtener predicciones más precisas. No obstante, la pregunta de cómo deben tratarse la tendencia y el ciclo estacional cuando se pronostica con modelos no lineales sigue abierta, ya que las soluciones planteadas en la literatura no son completamente satisfactorias.
El número máximo de rezagos fue obtenido como el mínimo orden P de un modelo autorregresivo, AR(P), tal que las autocorrelaciones de los residuales obtenidos al modelar la serie wt con dicho modelo no fueran significativamente diferentes de cero. Se encontró que P debería ser 24. Este es un criterio puramente heurístico con el cual se busca establecer el rezago más lejano que debería ser tenido en cuenta en la búsqueda del mejor modelo de predicción. En esta investigación se consideró que todos los modelos tenían como entradas los valores rezagos de la serie desde 1 hasta p para p=1, , P; nótese que no se consideraron todos los subconjuntos de rezagos que pueden obtenerse (224-1≈16,7 millones de combinaciones), ya que resulta inviable computacionalmente.
La bondad del ajuste de los modelos a las muestras de calibración y predicción fue medida mediante la sumatoria del error cuadrático medio (SSE, por sus siglas en inglés) de los residuales, et, ya definido en (4) y su desviación media absoluta (MAD, por sus siglas en inglés):
Donde et es la diferencia entre wt y el pronóstico obtenido con el modelo.
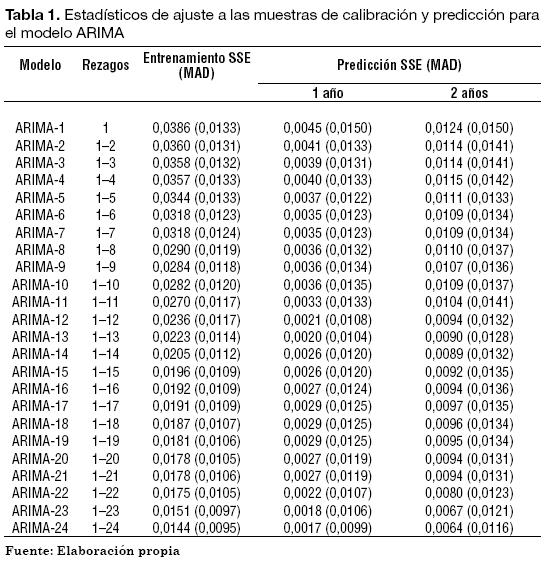
En primera instancia, se consideró que la serie wt podría ser pronosticada usando un modelo autorregresivo. Para ello, se estimaron modelos cuyas entradas corresponden a la serie wt rezagada desde 1 hasta P meses usando la información disponible hasta 2006:6. Con el modelo calibrado, se calculó el pronóstico para el próximo mes usando la muestra de predicción y se estimaron los estadísticos de ajuste presentados en la Tabla 1. El modelo ARIMA-24 presenta los propiamejores estadísticos de ajuste a la muestra de calibración y a las muestras de predicción de 12 meses y 24 meses; este es seguido, en su orden, por los modelos ARIMA-23 y ARIMA- 22. Teniendo en cuenta el error de entrenamiento (calibración) y los errores de predicción, se obtiene que la SSE calculada sobre la muestra de entrenamiento y los horizontes de 12 y 24 meses es de 0,0161 y 0,0208; respectivamente. Estos modelos son usados como un benchmark respecto a las otras aproximaciones no lineales consideradas.
En segunda instancia, se estimaron varios MLP cuyas entradas corresponden a la serie wt rezagada desde 1 hasta P meses y con H neuronas en la capa oculta, para H = 1, , 4. Para cada grupo de MLP con rezagos desde 1 hasta P y diferente número de neuronas en la capa oculta, se seleccionó el modelo con mejores estadísticos globales de ajuste. Los mejores modelos obtenidos para cada grupo de rezagos y sus correspondientes estadísticos de ajuste son presentados en la Tabla 2. El modelo MLP-19 presenta los mejores resultados de ajuste a la muestra de calibración (entrenamiento) con una SSE de 0,0181, seguido por el modelo MLP-23 con una SSE de 0,0191 (es decir, se da un incremento del 5%).
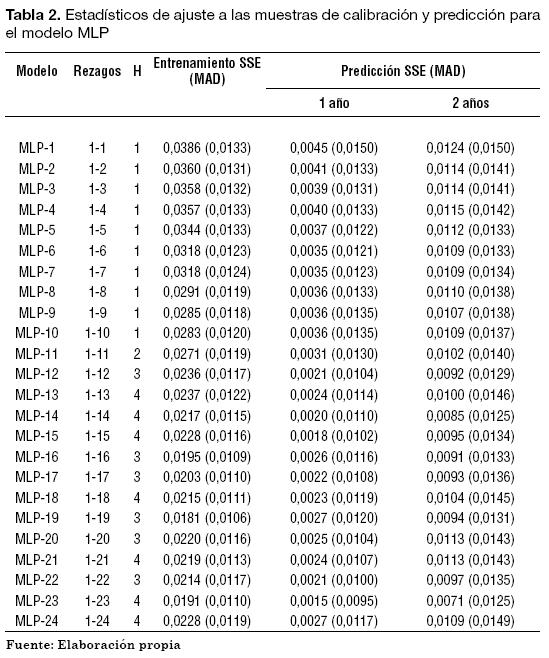
No obstante, el modelo MLP-23 presenta los mejores estadísticos de ajuste a las muestras de predicción con horizontes de 12 y 24 meses. Igualmente, este modelo es el que mejor se ajusta a la totalidad de los datos, con unas SSE de 0,0206 y 0,0262 cuando el estadístico es calculado usando simultáneamente la muestra de calibración y las muestras de predicción para los horizontes de 12 y 24 meses, respectivamente. En comparación con el mejor modelo ARIMA obtenido (ARIMA-24), el desempeño del modelo MLP-23 es inferior; sus SSE son del 133%, 88%, 111%, 128%, 126% para las muestras de entrenamiento, predicción a uno y a dos años y entrenamiento más predicción a uno y dos años, respecto los mismos estadísticos obtenidos por el modelo ARIMA-24.
Es de esperarse que el MLP tuviera un mejor comportamiento, o al menos igual, al del modelo ARIMA, pero acá se presenta una situación contraria; esto puede explicarse, al menos parcialmente, porque los modelos MLP y ARIMA son no intersectados; esto es, de un modelo no puede obtenerse el otro imponiendo restricciones sobre sus parámetros, causando que el MLP deba tener una arquitectura compleja para aproximar un comportamiento lineal que es fácilmente capturado por un ARIMA.
En tercera instancia, se estimaron varias ARNN siguiendo el mismo procedimiento descrito para los MLP. Se estimaron modelos cuyas entradas son la serie wt rezagada desde 1 hasta P meses y con 1 hasta 4 neuronas en la capa oculta. Los resultados obtenidos para el mejor modelo para cada grupo de rezagos considerados son presentados en la Tabla 3. En este caso, el desempeño de los modelos no es tan uniforme, y diferentes modelos podrían ser considerados como los mejores, dependiendo del criterio de selección usado. El modelo ARNN-18 presenta el mejor ajuste a la muestra de calibración con un SSE de 0,0085; pero tiene poco poder de pronóstico en comparación con otros de los modelos ARNN presentados en la Tabla 3. El modelo ARNN-23 presenta una arquitectura compleja con 4 neuronas en la capa oculta que le permite realizar la predicción más precisa entre todos los modelos ARNN considerados para los horizontes de 12 y 24 meses; en términos comparativos, los SSE obtenidos para el modelo ARNN-23 son el 47% y el 51% de los obtenidos para las muestras de predicción por el modelo ARNN-18. Al considerar el ajuste global a la muestra de datos, se encuentra que el modelo ARNN-18 presenta la menor SSE, con un valor de 0,0129, al considerar simultáneamente la muestra de calibración y la muestra de predicción de 12 meses. El modelo ARNN-24 tiene la menor SSE para la totalidad de los datos, con un valor de 0,0182; este corresponde al 80% del SSE (0,0230) obtenido por el modelo ARNN-18. Dados los estadísticos globales de ajuste, el modelo ARNN-24 presenta el mejor ajuste entre todos los modelos ARNN considerados.
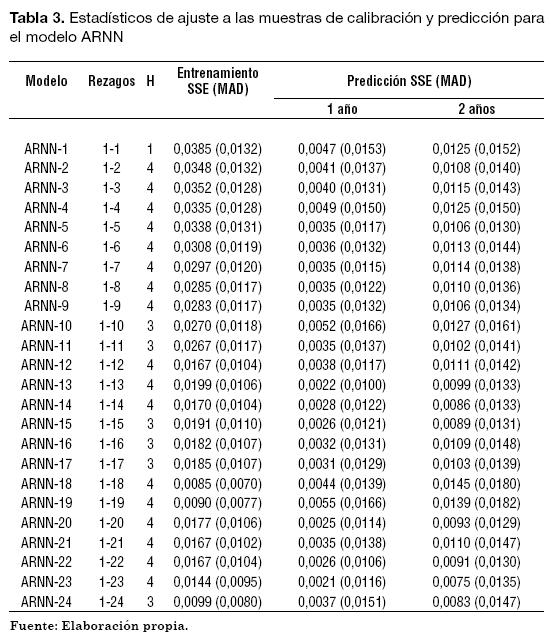
El modelo ARNN-24 revela el mejor ajuste a la muestra de calibración; las SSE obtenidas por los modelos ARIMA-24 y MLP-23 son el 192% y el 145% respecto al correspondiente estadístico para el modelo ARNN-24. De los tres modelos (ARNN-24, ARIMA-24 y MLP-23) la ARNN presenta las magnitudes más altas en los SSE para los horizontes de pronóstico de 12 y 24 meses, que corresponden a incrementos, de al menos, el 117% y 17% de los obtenidos por los modelos ARIMA-24 y MLP-23. No obstante, estos incrementos en los errores de predicción son compensados por el ajuste a la muestra de calibración, causando que el modelo ARNN-24 presente el mejor ajuste a la totalidad de los datos.
En el Gráfico 1 se presenta el logaritmo de la demanda y la predicción para el mejor modelo de cada tipo. La línea gris corresponde a los datos históricos y la línea negra a la predicción obtenida con cada modelo. Los datos para el gráfico fueron obtenidos realizando la transformación inversa de los procesos de diferenciación definidos en (4); esto es, se aplicaron los operadores de integración simple y estacional de periodo 12 para revertir el proceso realizado por la diferenciación. Para visualizar mejor la diferencia entre las predicciones obtenidas con cada modelo, se graficaron los residuos de la predicción para el siguiente mes (Gráfico 2).
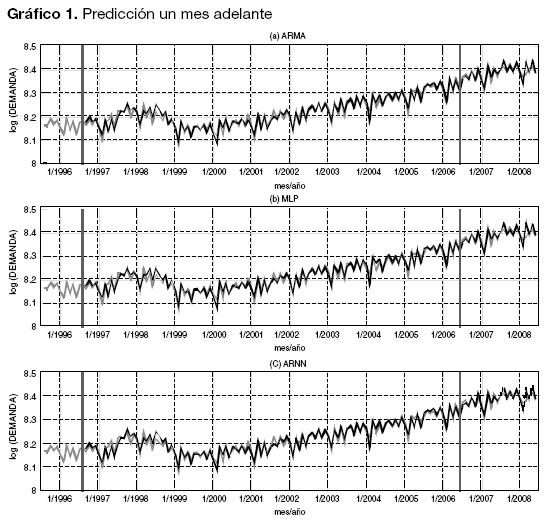
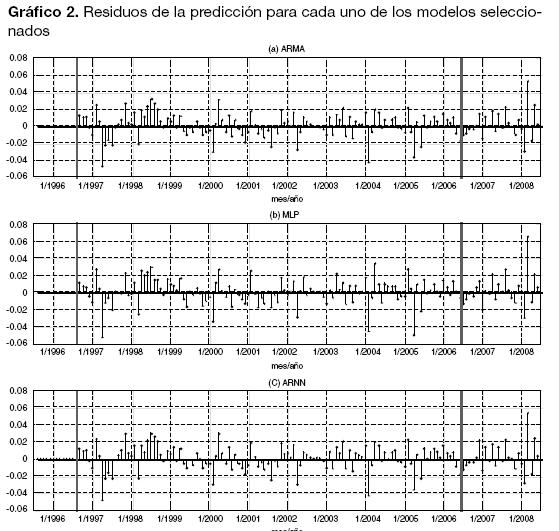
La comparación entre los pronósticos y los residuos obtenidos para cada modelo permite indagar mejor sobre el comportamiento puntual de cada modelo. Se observa en primera instancia, una similitud importante entre la magnitud y el signo de los adelanteresiduales para los modelos ARIMA-24 y ARNN-24 (explicada por la inclusión del modelo ARIMA en el ARNN), así como también, que este patrón se conserva para el modelo MLP-23 sólo para algunas regiones. A simple vista, se nota que el modelo MLP-23 presenta errores mayores para las observaciones 1997:4, 2005:2, 2005:4 y 2008:3. Igualmente, la magnitud y el signo de los residuos del modelo MLP-23 difieren respecto a los de los otros modelos en los años 1998, 2002 y 2004; esta es, posiblemente, la causa de que el desempeño del modelo MLP-23 sea inferior respecto a los modelos ARIMA y ARNN. Los residuos de los modelos ARIMA-24 y ARNN-24 tienen el mismo signo, pero se presenta una reducción de su magnitud para el modelo ARNN-24 haciendo que este último tenga un mejor ajuste a la muestra de calibración. Las diferencias más importantes entre ambos modelos (ARIMA-24 y ARNN-24) para la muestra de predicción se observan en 2006:12 y 2007:2, lo que explica la diferencia presentada en los estadísticos de ajuste. Esto permite concluir que la componente MLP del modelo ARNN captura relaciones no lineales sutiles que el modelo ARIMA por sí solo no puede manejar.
3. CONCLUSIONES
En este artículo se compara el desempeño de un modelo ARIMA, un perceptron multicapa y una red neuronal autorregresiva para pronosticar la demanda mensual de electricidad en Colombia para el siguiente mes adelante. Los datos disponibles fueron divididos en dos conjuntos, el primero para estimar los parámetros del modelo y el segundo para la capacidad de predicción por fuera de la muestra de calibración. Los resultados revelan que la red neuronal autorregresiva es capaz de pronosticar la demanda con mayor precisión que los otros dos modelos cuando la totalidad de los datos es considerada. Este resultado señala que existe una componente sutil de carácter no lineal en la información que el modelo ARIMA no puede capturar debido a su naturaleza lineal. También se encontró que el MLP presenta un comportamiento diferente, tal como lo evidencia la diferencia entre la magnitud y el signo de sus residuales cuando son comparados con los residuales obtenidos por los otros modelos considerados.
Los resultados reportados aquí, permiten recomendar el uso de de los modelos ARNN para la predicción de la demanda de electricidad. No obstante, en este trabajo no se agotan todas las posibilidades respecto a la investigación realizada. Es necesario indagar si otros modelos no lineales pueden pronosticar con mayor precisión la serie estudiada, tales como diferentes tipos de redes neuronales difusas y nuevos tipos de arquitecturas de redes neuronales artificiales.
NOTAS AL PIE DE PÁGINA
1. Neón es un servicio de información gratuito que permite la consulta interactiva de las principales variables relacionadas con la evolución del mercado eléctrico colombiano; este servicio es prestado por XM Compañía de Expertos en Mercados S. A. ESP, a través de su página WEB (www.xm.com.co)
REFERENCIAS BIBLIOGRÁFICAS
1. Abdel-Aal, R. y Al-Garni, A. (1997). Forecasting monthly electric energy consumption in eastern Saudi Arabia using univariate time series analysis. Energy, 22(11), 10591069.
2. Abdel-Aal, R., Al-Garni, A. y Al-Nassar, Y. (1997). Modelling and forecasting monthly electric energy consumption in eastern Saudi Arabia using abductive networks. Energy, 22(9), 911921.
3. Al-Saba, T. y El-Amin, I. (1999). Artificial neural networks as applied to long-term demand forecasting. Artificial Intelligence in Engineering, 13(2), 189197.
4. Barrientos, A.F., Olaya, J. y González, V.M. (2007). Un modelo spline para el pronóstico de la demanda de energía eléctrica. Revista Colombiana de Estadística, 30(2), 187-202.
5. Beenstock, M., Goldin, E. y Nabot, D. (1999). The demand for electricity in Israel. Energy Economics, 21(2), 168183.
6. Benavente, J., Galetovic, A., Sanhueza, R. y Serra, P. (2005). Estimando la demanda residencial por electricidad en Chile: El consumo es sensible al precio. Cuadernos de Economía, 42, 3161.
7. Box, G.E.P. y Jenkins, G.M. (1976). Time Series Analysis: Forecasting and Control. San Francisco, CA: Prentice Hall.
8. Castaño, E. (2008). Reconstrucción de datos de series de tiempo: una aplicación a la demanda horaria de electricidad. Revista Colombiana de Estadística, 30(2), 247263.
9. Chaveza, S.G., Bernata, J.X. y Coallab, H.L. (1999). Forecasting of energy production and consumption in Asturias (northern Spain). Energy, 24(3), 183198.
10. Clements, M.P., Franses, P.H. y Swanson, N.R. (2004). Forecasting economic and financial time-series with non-linear models. International Journal of Forecasting, 20(2), 169-183.
11. Conejo, A.J., Contreras, J., Espínola, R. y Plazas, M.A. (2005). Forecasting electricity prices for a day-ahead pool-based electric energy market. International Journal of Forecasting, 21(3), 435-462.
12. Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Mathematics of Control: Signals and Systems, 2, 202314.
13. Ediger, V. y Tatlidil, H. (2002). Forecasting the primary energy demand in turkey and analysis of cyclic patterns. Energy Conversion and Management, 43(4), 473487.
14. Egelioglu, F., Mohamad, A. y Guven, H. (2001). Economic variables and electricity consumption in northern Cyprus. Energy, 26(4), 355362.
15. Franco, C.J., Velásquez, J.D. y Olaya, Y. (2008). Caracterización de la demanda mensual de electricidad en Colombia usando un modelo de componentes no observables. Cuadernos de Administración, 21, 36, 221-235
16. Funahashi, K. (1989). On the approximate realization of continuous mappings by neural networks. Neural Neworks, 2, 183192.
17. Ghiassi, M., Saidane, H. y Zimbra, D.K. (2005). A dynamic artificial neural network model for forecasting time series events. International Journal of Forecasting, 21, 341-362.
18. Harris, J. y Liu, L.M. (1993). Dynamic structural analysis and forecasting of residential electricity consumption. International Journal of Forecasting, 9(4), 437455.
19. Harvey, A. (1989). Forecasting, structural time series models and the Kalman filter. Cambridge, MA: Cambridge University Press.
20. Heravi, C., Osborn, D.R. y Birchenhall, C.R. (2004). Linear versus neural network forecasts for European industrial production series. International Journal of Forecasting, 20(3), 435-446.
21. Hornik, K., Stinchcombe, M. y White, H. (1989). Multilayer feedforward networks are universal approximators. Neural Networks, 2, 359366.
22. Kaastra, I. y Boyd, M. (1996). Designing a neural network for forecasting financial and economic series. Neurocomputing, 10, 215236.
23. Lee, T.H., White, H. y Granger, C.W.J. (1993). Testing for neglected nonlinearity in time series models. Journal of Econometrics, 56, 269-290.
24. Masters, T. (1993). Practical Neural Network Recipes in C++ (1ra. ed.). San Diego, CA: Academic Press Professional.
25. Masters, T. (1995). Neural, Novel and Hybrid Algorithms for Time Series Prediction (1ra ed.). New York, NY: John Wiley and Sons.
26. Medina, S. y García, J. (2005). Predicción de demanda de energía en Colombia mediante un sistema de inferencia difuso neuronal. Revista Energética, 33, 1524.
27. Mirasgedis, S., Sarafidis, Y., Georgopoulou, E., Lalas, D., Moschovits, M., Karagiannis, F. y Papakonstantinou, D. (2006). Models for mid-term electricity demand forecasting incorporating weather influences. Energy, 31(23), 208227.
28. Mohamed, Z. y Bodger, P. (2005). Forecasting electricity consumption in New Zealand using economic and demographic variables. Energy, 30(10), 18331843.
29. Murillo, J., Trejos, A. y Carvajal, P. (2003). Estudio del pronóstico de la demanda de energía eléctrica utilizando modelos de series de tiempo. Scientia et Technica, 23, 3742.
30. Murray, F. y Ringwood, J. (1994). Improvement of electricity consumption forecasts using temperature inputs. Simulation Practice and Theory, 2(2), 121139.
31. Nasr, G., Badr, E. y Dibeh, G. (2000). Econometric modelling of electricity consumption in post-war Lebanon. Energy Economics, 22(6), 627640.
32. Nasr, G., Badr, E. y Joun, C. (2003). Backpropagation neural networks for modelling gasoline consumption. Energy Conversion and Management, 44, 893905.
33. ONeill, B. y Desai, M. (2005). Accuracy of past projections of us energy consumption. Energy Policy, 33(8), 979993.
34. Saab, S., Badr, E. y Nasr, G. (2001). Univariate modelling and forecasting of energy consumption: the case of electricity in Lebanon. Energy, 26(1), 114.
35. Sarle, W. (1994). Neural networks and statistical models. Documento presentado en The Nineteenth Annual SAS Users Group International Conference, Cary, NC, Estados Unidos.
36. Steiner, F. (2000). Regulation, industry structure and performance in the electricity supply industry. OECD Economics Department Working Papers, 238.
37. Stoft, S. (2002). Power System Economics. New York, NY; Wiley-Interscience.
38. Swanson, N. y White, H. (1997a). Forecasting economic time series using flexible versus fixed specification and linear versus nonlinear econometric models. International Journal of Forecasting, 13(4), 439-461.
39. Swanson, N. y White, H. (1997b). A model selection approach to real time macroeconomic forecasting using linear models and artificial neural networks. The Review of Economics and Statistics, 79(4), 540-550.
40. Teräsvirta, T., Lin, C.F. y Granger, C.W.J. (1993). Power of the neural network linearity test. Journal of Time Series Analysis, 14, 209-220.
41. Teräsvirta, T., van Dijk, D. y Medeiros, M. C. (2005). Linear models, smooth transition autoregressions, and neural networks for forecasting macroeconomic time series: A re-examination. International Journal of Forecasting, 21(4), 755-774.
42. Tserkezos, E. (1992). Forecasting residential electricity consumption in Greece using monthly and quarterly data. Energy Economics, 14(3), 226232.
43. Unidad de Planeación Minero-Energética UPME. (2004). Plan de Expansión Preliminar 20042018. Bogotá, Colombia: Autor.
44. White, H. (1989). An additional hidden unit test for neglected nonlinearity in multilayer feedforward networks. Proceedings of the International Joint Conference on Neural Networks, 2, 451-455.
45. Zhang, G., Patuwo, B. y Hu, M. (1998). Forecasting with artificial neural networks: the state of the art. International Journal of Forecasting, 14, 3562.
46. Zhang, G. y Qi, M. (2005). Neural network forecasting for seasonal and trend time series. European Journal of Operational Research, 160(2), 501-514.