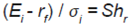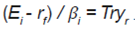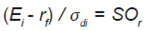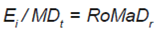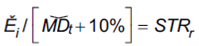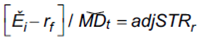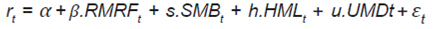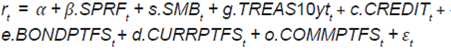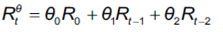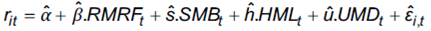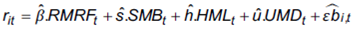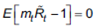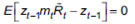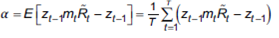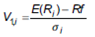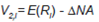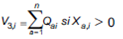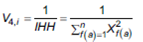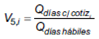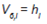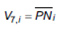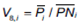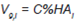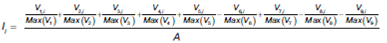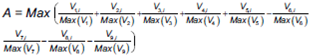1. Introducción
Los modelos de equilibrio, en general, proponen un conjunto de atributos vinculados al riesgo de los activos financieros, que si no se puede diversificar, debería ser recompensado por el mercado. Entonces, una gestión con buen desempeño financiero es considerada aquella con rendimientos superiores, controlando por el nivel de riesgo asumido. En este sentido, luego del trabajo seminal de Jensen (1968) se ha desarrollado un conjunto de métodos para evaluar el desempeño de los fondos, a partir de las habilidades de sus administradores. Estas técnicas pueden clasificarse en dos grandes grupos: a) evaluaciones del desempeño basadas en los rendimientos de los fondos y b) evaluaciones del desempeño basadas en las tenencias (participaciones) de los fondos. Las técnicas indicadas presentan debilidades y fortalezas. Las evaluaciones del desempeño basadas en los rendimientos se destacan en situaciones donde no se revela suficiente información relativa a la composición del fondo y su estrategia de inversión; por lo general en la mayoría de los fondos de inversión los datos relativos a rendimientos son revelados con mayor frecuencia que la composición y participación en el fondo. Las medidas existentes, que nacen mayoritariamente de los modelos de equilibrio tradicionales y trasladan sus supuestos y limitaciones, son la motivación para el desarrollo de un índice multifactorial que permita realizar un ordenamiento de inversiones financieras de acuerdo a su desempeño, teniendo en cuenta un conjunto de factores y no alguno aisladamente.
En este contexto, el objetivo del artículo consiste en desarrollar un método integral para la elaboración e implementación de un índice de desempeño financiero. La medida, además de analizar las métricas clásicas vinculadas al rendimiento y riesgo, incorpora elementos vinculados con la estructura del fondo mediante variables que ponderan: diversificación, liquidez, costos transaccionales, umbrales de rendimiento, tamaño y apalancamiento financiero. Su aplicación se ilustra y valida mediante un estudio de caso sobre el universo de fondos comunes de inversión (FCI) cotizantes en Argentina durante el año 2016, a partir de información secundaria. El resultado obtenido es un ordenamiento consistente basado en el desempeño observado de las nueve variables que integran la medida.
El trabajo se estructura de la siguiente forma: en la sección 2 se resumen los modelos y medidas de desempeño financiero, clasificadas en ratios, análisis econométrico, estudio de tenencias y estructuras de los fondos. En la sección 3 se presenta la medida de desempeño propuesta en el trabajo, la cual consiste en el desarrollo de un índice multidimensional. En el apartado 4 son expuestas las cuestiones metodológicas y de aplicación relativas a la implementación del índice. A tales efectos fue seleccionada como unidad de análisis el conjunto de fondos abiertos negociados en el mercado de capitales argentino, considerando datos correspondientes al año 2016. Los resultados y ordenamiento correspondiente al ranking de fondos arrojado por el índice se presentan en la sección 5. Finalmente, el apartado 6 presenta las conclusiones del trabajo.
2. Modelos para evaluar el desempeño de los fondos de inversión
2.1 Principales modelos de equilibrio
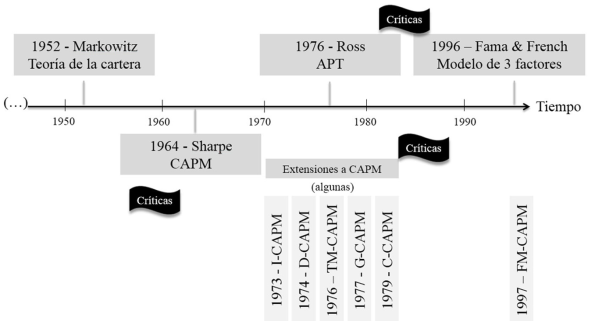
El origen de la evaluación del desempeño de los activos financieros se remonta a los modelos clásicos de equilibrio (figura 1), que nacen con la Teoría de la Cartera (Markowitz, 1952). A partir de este modelo de equilibrio parcial, se desarrolla un concepto clave que es el de eficiencia (Tobin, 1958), el cual se refiere a la condición de las carteras compuestas por un portafolio eficiente óptimo (conocido como cartera de mercado) que diversifica al máximo el riesgo específico de los activos individuales, y un activo libre de riesgo. Dichas carteras se situan sobre la conocida Línea de Mercado de Capitales (CML, por sus siglas en inglés de Capital Market Line); la participación de ambos tipos de inversión dentro de la cartera dependerá de la aversión al riesgo de cada inversor.
Fuente: elaboración propia.
Figura 1 Línea de tiempo de los modelos de equilibrio principales
Posteriormente, Sharpe (1964) plantea el modelo de valuación de activos de capital (CAPM, por sus siglas en inglés de Capital Assests Pricing Model), en donde se considera que el mercado solo paga por el riesgo sistemático o no diversificable de cada activo, cuya medida se conoce como coeficiente beta (β), y explica la variabilidad de los rendimientos esperados de un activo como consecuencia de la variabilidad de los rendimientos de la cartera de mercado. De este modo, surge el concepto de equilibrio, a partir de la comparación del rendimiento requerido o teórico de cada activo financiero, que surge de la línea de mercado de valores (SML, por sus siglas en inglés de Security Market Line) con el rendimiento observado o estimado del activo. La diferencia entre ambos rendimientos se conoce como coeficiente alfa. Si el activo se encuentra valuado en equilibrio ambos rendimientos coinciden, caso contrario se está en presencia de sobre o subvaluaciones, por lo que el coeficiente alfa es diferente de cero (negativo o positivo, respectivamente).
El modelo CAPM recibió duras críticas (Roll, 1977) que dieron lugar a la aparición de diversas extensiones al modelo, las que difieren principalmente en el factor de riesgo sistemático que utilizan como variable explicativa del rendimiento de los activos financieros. Entre ellas se destacan, cronológicamente, el modelo CAPM con desvíos negativos a partir del concepto de semi-varianza (D-CAPM, por downside CAPM) planteado por Hogan y Warren (1974); CAPM internacional o global (G-CAPM) de Stehle (1977); CAPM basado en consumo (C-CAPM) de Breeden (1979); entre otros.
También aparecieron extensiones de CAPM que incorporaron los momentos de orden superior; por ejemplo el CAPM de tres momentos que incorpora la asimetría (TM-CAPM, por las siglas en inglés de three-moment CAPM) a partir del trabajo seminal de Kraus y Litzenberber (1976) y CAPM de cuatro momentos que agrega tanto la asimetría como la curtosis (FM-CAPM, por las siglas en inglés de four-moment CAPM) propuesto por Fang y Lai (1997).
Con relación al número de factores explicativos, surgieron modelos alternativos al CAPM, tales como CAPM intertemporal (I-CAPM) propuesto por Merton (1973), la Teoría de Fijación de Precios por Arbitraje (APT, por las siglas en inglés de Arbitrage Pricing Theory) (Ross, 1976; Roll y Ross, 1980) y el modelo de los tres factores de Fama y French (1996). En el modelo APT el rendimiento de un activo depende de múltiples factores, no sólo de la prima por riesgo de mercado como en el CAPM, surgiendo estos de estimaciones empíricas, siendo variables en número y naturaleza. Habitualmente, los mismos se encuentran asociados a estados que describen la economía, como el tipo de interés, la inflación, el crecimiento del producto interno bruto, el precio de alguna materia prima o divisa, entre otros. Por el contrario, el modelo de Fama y French (1996) especifica tres factores explicativos y nominados como variables explicativas: la prima por riesgo de mercado, tal como CAPM; un diferencial de rendimiento entre carteras de acciones de firmas pequeñas versus carteras de acciones de grandes empresas; y un diferencial de rendimiento entre carteras de acciones con elevado ratio valor libro a valor de mercado versus carteras de acciones con bajo ratio. Es importante aclarar que los dos factores adicionales que consideran estos autores en el modelo se refieren a riesgos específicos de un grupo de activos y, por lo tanto, reflejan riesgos no sistemáticos o diversificables, que se pueden interpretar como ineficiencias del mercado. Se debe tener presente que los modelos multifactoriales han sido testeados empíricamente con resultados muy satisfactorios en cuanto a la eficacia para explicar rendimientos de los activos financieros.
2.2. El desempeño de los fondos comunes como activos de inversión
Desde la perspectiva de la práctica profesional y de los trabajos académicos en materia de desempeño de fondos, estos se pueden clasificar en dos grandes grupos: comunes (mutual) y de cobertura (hedge). Se entiende que un fondo común es una cartera compuesta por un conjunto de fondos aportados por inversores y aplicados a diferentes activos financieros como acciones, bonos e instrumentos del mercado de dinero. Estos son gerenciados por administradores con el fin de obtener rendimientos y ganancias de capital. En su estructura y estrategia activa las tenencias se mantienen o venden con el fin de cumplir los objetivos de inversión indicado en el prospecto de creación. Por otro lado los fondos de cobertura son una especie compleja de fondos que utilizan estrategias activas para obtener rendimientos diferenciales. Estos son administrados de manera agresiva y emplean derivados como apalancamiento financiero (ventas cortas) con el fin de obtener rendimientos equiparables o por encima de un comparable (benchmark). Cabe destacar que los fondos de cobertura se caracterizan por su complejidad y por ser destinados a inversores institucionales, dado que estos fondos están sujetos a una menor regulación.
Todas las medidas de desempeño presentan un común denominador y este consiste en la premisa de evaluación que utilizan. De hecho, se considera buen desempeño aquel caso que arroje resultados positivos originados por estrategias de administración activa de la cartera que no puedan ser fácilmente replicables por inversores desinformados. En otras palabras, el desempeño positivo y la recompensa no van de la mano de estrategias simples, mecánicas y pasivas. Las características que debe reunir el activo que será utilizado como comparable y las condiciones a cumplir por una medida para evaluar desempeño son las siguientes:
Comparable (benchmark): en relación con su uso como medida de referencia para evaluar el rendimiento de un fondo, este debe cumplir las siguientes condiciones (Bailey, 1995): a) específico: su integración y participaciones deben estar especificadas; b) negociable: sujetos a compra - venta en los mercados; c) mensurables: debe ser posible computar medidas de rendimientos válidas sobre la observación de datos de mercado; d) pertinente: las características del comparable deben ajustarse a las estrategias de administración del fondo objeto de evaluación; e) evaluable: el administrador del fondo debe ser capaz de proyectar potenciales rendimientos de la medida de benchmark.
Condiciones de una medida de desempeño: respecto a las medidas de desempeño Chen y Knez (1996) señalan cuatro propiedades que estas deben observar: a) ajuste: en la medición deben capturar las estrategias activas o pasivas que razonablemente sean empleadas por un inversor no informado con variables de control y asignarle una ponderación de cero a los fondos con estas estrategias ''simples''; b) escalabilidad: las combinaciones lineales de las diferentes medidas o indicadores de desempeño deben ser iguales al resultado que arroja medir la combinación lineal de las carteras que integran el fondo; c) continuidad: dos gestiones de fondos con estrategias de gestión similares deben obtener resultados semejantes; d) monotonicidad: la medida de desempeño debe valorar en mayor medida las capacidades positivas de los administradores. Estas propiedades evitan que las medidas de desempeño terminen ponderando positivamente a gestiones de cartera deficientes y que los inversores no paguen honorarios por estrategias que ellos fácilmente podrían llevar a cabo (Wermers, 2000, 2011).
En las siguientes subsecciones son expuestas diferentes técnicas para evaluar el desempeño de carteras de inversión agrupadas en, por una parte, modelos que analizan el desempeño a partir del estudio de los rendimientos, y por otra, aquellos que lo hacen estudiando la composición de inversiones del fondo.
2.3. Medidas de desempeño basadas en el estudio de rendimientos
Para este tipo de estudio es imperativa la existencia de datos de mercado acerca del fondo a evaluar, que permita interpretar a partir del comportamiento de los rendimientos, información relativa al desempeño del fondo, estrategias y perfil riesgo-rendimiento. En este caso, se deben aplicar modelos econométricos cuyos supuestos de partida descansan en el conocimiento del perfil de riesgo de los administradores, empleo de comparables apropiados, definición del punto de ruptura definido por los administradores en relación al riesgo sistemático e idiosincrático del fondo, definición a priori de las estrategias dinámicas para asumir riesgos y la distribución de probabilidad que siguen los retornos. Estos modelos se clasifican en dos grupos: medidas tradicionales y análisis econométrico.
2.3.1. Medidas tradicionales para evaluar desempeño: los ratios
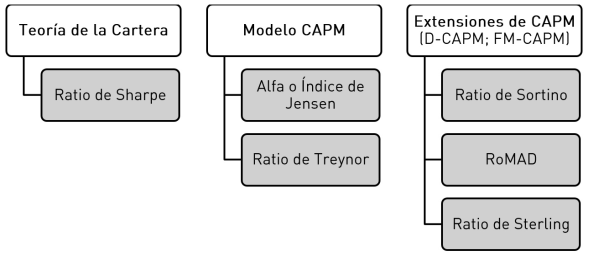
A continuación se presentan algunas de las primeras y clásicas medidas para evaluar el desempeño de inversiones en activos financieros y fondos comunes. Estas medidas emergen de los conceptos de la clásica teoría de la cartera (Markowitz, 1952, 1959) y de las derivaciones de los modelos de equilibrio para la valuación de activos (Wilmott, 2009), como se puede observar en la figura 2. Conjuntamente con las medidas estadísticas como volatilidad, r2 y coeficiente beta, los ratios clásicos para medir desempeño son el coeficiente Alfa o Índice de Jensen, ratio de Sharpe, ratio de Treynor, ratio de Sortino, RoMaD (de las siglas en inglés de return over maximum drawdown) y ratio de Sterling. A continuación se revisará cada uno de ellos.
Fuente: elaboración propia.
Figura 2 Modelos de equilibrio y ratios para evaluación de desempeño financiero.
Alfa: es una clásica medida de desempeño para evaluar rendimientos anormales o en exceso. En la práctica tiene dos usos muy difundidos. El primero en el marco del modelo CAPM, ya que mide rendimientos anormales o en exceso de un activo en particular, por sobre los que prescribe el modelo indicado. En el contexto de los modelos de equilibrio, alfa es conocida como Índice de Jensen (Jensen, 1968), que no debe confundirse con la desigualdad de Jensen1. El índice de Jensen mide los rendimientos por encima o debajo a los proyectados por el modelo CAPM. Es decir, si ri representa los rendimientos observados del activo y re los requeridos o teóricos según el modelo, el índice de Jensen o alfa es: α =ri-re , siendo re = rf +( Em - rf ). βi , representando rf la tasa de rendimiento libre de riesgo, Em el rendimiento de la cartera del mercado y βi el coeficiente beta del activo2. En segundo término es una medida de desempeño de fondos de inversión, ya que compara el rendimiento del fondo contra una medida seleccionada como comparable. La denominación de alfa se asigna al diferencial entre los rendimientos del fondo en relación a los rendimientos del comparable, también conocidos como rendimientos anormales o extraordinarios.
Al emplear esta medida de desempeño se supone que la cartera es eficiente, se encuentra diversificada, y por ende ha eliminado el riesgo asistemático. Al ser una medida que surge de un benchmark, su resultado indica el valor que se agrega o se sustrae al fondo producto de la estrategia de los administradores. En otras palabras, es el rendimiento generado por acciones particulares del inversor, no del mercado. La medida presenta limitaciones, entre ellas la falta de especificidad, ya que si bien es empleada para evaluar una diversidad de activos financieros, a menudo se cae en la tentación de usarlo para realizar comparaciones entre fondos que poco tienen que ver entre sí. Por lo tanto, es de utilidad en la medida en que la comparación se realice entre clases de activos. Asimismo, como la medida se obtiene a partir de un activo comparable es importante la correcta elección del último y su continua estimación, ya que la estructura de los fondos y carteras de inversiones, sujetas a una administración activa, están condicionadas a un continuo rebalanceo.
Ratio de Sharpe: nace a partir de la Teoría de la Cartera y se conoce también como precio del riesgo. Es una medida estándar que permite jerarquizar inversiones en relación con dos dimensiones: rendimiento-riesgo. El ratio es el rendimiento promedio ganado en exceso sobre la tasa de rendimiento libre de riesgo por unidad de riesgo, permitiendo evaluar las estrategias de inversión en relación a la toma de riesgos. La idea que subyace detrás de la medida es la siguiente: a mayor ratio más atractivo es el rendimiento ajustado por riesgo de la cartera. Su forma estructural consiste en un cociente:
(1)
Donde Ei representa rendimientos esperados (ex-ante) u observados (ex-post) de la cartera, rf es la tasa de rendimiento libre de riesgo y σi es la volatilidad de la misma medida a través de su desvío estándar.
Una adaptación la constituye la medida conocida como el ratio de Treynor (Treynor, 1965), donde la volatilidad es sustituida por βi , midiendo rendimientos en exceso por unidad de riesgo sistemático, como se observa a continuación:
(2)
Una de las principales aplicaciones del ratio de Sharpe consiste en estudiar cómo varía el ratio a medida que cambia la estructura de la cartera3. No obstante, la medida no es apropiada en el caso de carteras integradas por derivados financieros, como opciones o warrants, pues en este caso las relaciones riesgo-rendimiento dejan de ser lineales y por lo tanto emergen momentos estocásticos de orden superior, como asimetría y curtosis. Para sortear los inconvenientes indicados se disponen de dos medidas complementarias para evaluar desempeño: Ratio de Sortino y RoMaD.
Ratio de Sortino: su nombre lo debe a Sortino y Price (1994). La medida tiene un razonamiento similar al ratio de Sharpe, es decir a mayor valor mejor desempeño, ya que mide el rendimiento obtenido por riesgo de mala calidad, resultado de calcular la semidesviación típica de los rendimientos negativos. El ratio sigue la siguiente estructura:
(3)
Lo único que varía respecto del ratio de Sharpe es σdi , que representa el riego de valores inferiores o volatilidad asociada a rendimientos negativos4. Esta medida permite trabajar mejor con momentos estocásticos de orden superior, asimetría y curtosis, una importante desventaja en ratios como el Índice de Jensen, el ratio de Sharpe y el de Treynor.
RoMaD: este ratio es una adaptación de la medida empleada en el precio de las materias primas, desarrollada por Young (1991). Es una medida complementaria a los ratios anteriores, siendo el cociente entre los rendimientos y la diferencia entre un punto de máximo de rendimiento y un punto subsecuente de bajo desempeño, tal que:
(4)
Donde Ei representa el rendimiento esperado u observado del fondo y MDt la máxima caída. Esta es una de las medidas más utilizadas en la actualidad para analizar la evolución y el riesgo de fondos de cobertura, ya que una de las maneras de estimar la exposición al riesgo es evaluar el patrón de pérdidas o rendimientos negativos del fondo durante un periodo considerable de tiempo. Además, permite incorporar los momentos estocásticos de orden superior como asimetría y curtosis de la distribución de probabilidad de rendimientos. El rendimiento sobre la máxima caída para un periodo determinado permite evaluar el siguiente interrogante: ¿Se está dispuesto a soportar una pérdida de MDt a cambio de un Ei , exponiéndose durante un determinado periodo de tiempo?5
Ratio de Sterling: este índice presenta su denominación debido a la propuesta de Deane Sterling Jones (Sortino y van der Meer, 1991; Bacon, 2013). Es otra medida de rendimiento ajustado por riesgo para evaluar desempeño de carteras. Es igual al promedio compuesto (media geométrica) de la tasa de rendimiento efectiva anual de los últimos tres años calendarios dividido por el promedio de las máximas caídas de cada uno de esos tres años más un 10% de ajuste. Su estructura es:
(5)
El valor del 10% es un ajuste empírico, ya que se compara el desempeño y se carga de riesgo extra en función al rendimiento libre de riesgo de las letras del Tesoro norteamericano (T-bills) que en el año 1981 era del 10%. La versión ajustada del ratio y aggiornada de la medida se asemeja al ratio de Sharpe, así:
(6)
Al igual que en los casos precedentes un alto ratio indica un correcto desempeño frente a la exposición al riesgo del fondo, siendo su interpretación similar a los ratios anteriores.
2.3.2. Modelos econométricos
En este grupo se encuentran los modelos que aplican técnicas econométricas que van desde el análisis multifactorial mediante regresiones, pasando por técnicas de bootstrap con el fin de analizar el comportamiento de los rendimientos y determinar factores que explican rendimientos en exceso de los FCI, producidos por estrategias activas exitosas en la administración del fondo. A continuación se presentan los principales modelos.
Modelos basados en factores: inspirados en los modelos multifactoriales presentados en la sección 2.1 (Ross, 1976; Fama y French, 1996), los primeros desarrollos se concentraron en determinar qué factores describen estrategias exitosas de administración de fondos. Uno de los primeros modelos de amplia difusión para analizar el desempeño en la administración de fondos de renta variable es el conocido como modelo de cuatro factores de Carhart (1997).
(7)
Donde rt es el rendimiento mensual de la cartera administrada en exceso por sobre el del activo libre de riesgo ( rf ), RMRFt es el rendimiento en exceso de una cartera que replica al mercado donde los activos la integran con base en sus participaciones en el valor total de la cartera, mientras que las carteras SMBt , HMLt y UMDt son portafolios cuyos activos participan en función del valor, replicando rendimientos por tamaño, valor de mercado a valor de libros y el momentum definido a partir de los rendimientos del último año. El modelo tiene sus fundamentos en los resultados de las investigaciones de Fama y French (1992, 1993 y 1996) y Jegadeesh y Titman (1993).
En esta familia de medidas de desempeño y orientado específicamente a los fondos de cobertura (hedge) se encuentra el modelo de siete factores de Fung y Hsieh (2004) .
(8)
Donde los factores son: SPRFt se refiere a los rendimientos del índice Standard & Poor's 500 menos la tasa libre de riesgo, SMBt son los rendimientos de la cartera Wilshire calculados por diferencia entre rendimientos de empresas pequeñas y grandes, midiendo el tamaño por la capitalización bursátil, TREAS10 ytt se refiere a cambios en los rendimientos de los bonos soberanos de Estados Unidos a 10 años, CREDITt son los cambios en el diferencial de rendimientos entre bonos calificados por Moody's como Baa y los rendimientos de los bonos soberanos a 10 años y BONDPTFSt , CURRPTFSt y COMMPTFSt son los rendimientos de tres estrategias clásicas derivadas del mercado de bonos, monedas y materias primas. Para evitar las distorsiones de las bases de datos de los fondos, los comparables son elaborados a partir de rendimientos de activos individuales. Los modelos del tipo de las ecuaciones 7 y 8 parten de un conjunto de supuestos duros. En el caso de los rendimientos de activos y factores, se supone distribución normal, de forma idéntica e independiente (NIID, normally identical independental distributed) y que la varianza se mantiene constante.
El problema del aplanamiento de rendimientos informados por los administradores de fondos fue confirmado por evidencia empírica a partir de trabajos como el de Bollen y Pool (2009). Esta conducta de revelación de información se fundamenta en las preferencias que tienen los inversores, suponiendo que rendimientos planos se correlacionan con menor volatilidad. Por ejemplo un fondo con rendimientos observados del 12% y -8% puede informar tasas compuestas de rendimientos equivalentes al +/- 1,5%, y esto tiene impacto directo sobre dos medidas inobservables en el mercado, como la volatilidad y la métrica para cuantificar la exposición a los factores de riesgo del fondo. Como consecuencia de ello, Getmansky, Lo y Makarov (2004) proponen que los modelos como los planteados en las ecuaciones 7 y 8 sean ajustados para capturar el aplanamiento de rendimientos. Estos sugieren incorporar un ajuste de rendimientos rezagados y actuales sobre las ecuaciones para capturar el efecto del aplanamiento.
(9)
Donde θ0+θ1+ θ2 = 1, en este caso para dos rezagos.
Estudio de residuos mediante bootstrap (alfas no normales): la serie de rendimientos de los fondos a menudo presenta comportamientos no consistentes con el uso de herramientas econométricas tradicionales, ya sea por su forma de distribución o por la elección de los factores de riesgo. Existen algunos hechos estilizados en los rendimientos de los fondos comunes de inversión. En principio existe evidencia respecto de la existencia de asimetrías y curtosis, particular cuestión que si no se emplean técnicas apropiadas, en lugar de las tradicionales herramientas basadas en supuestos de normalidad, se puede incurrir en mediciones erróneas. Una herramienta para ajustar la medida de desempeño alfa es la propuesta por Kosowski, Timmermann, Wermers y White (2006) . En esta aplican la técnica de bootstrap para evaluar desempeños frente a distribuciones de probabilidad no normales, generando alfas sólidos estadísticamente mediante el análisis de residuos a través de la técnica de bootstrap. Su inquietud se fundamenta en la hipótesis de que administradores con alfas extremos (altos-bajos) en relación al promedio del grupo, tienden a tener distribuciones de rendimientos con altos niveles de curtosis y asimetría. Para corroborar esto se implementa bootstrap mediante el modelo de cuatro factores de Carhart (1997). La aplicación de la técnica es similar a la de otros modelos, pero desarrollando un procedimiento novedoso en los pasos a seguir para aplicar el modelo de benchmark. Primero se emplea el modelo de Carhart para calcular los alfas, mediante ajuste por mínimos cuadrados, incorporando factores y estimando residuos. Para ello se emplean las series mensuales de exceso de rendimientos sobre las letras del Tesoro norteamericano (T-bills) por fondo.
(10)
Para cada serie se estiman los coeficientes, los residuos y los estadísticos correspondientes a los alfas estimados, donde
T0,I
;
T1,I
, son los datos para el primero y último mes. Seguidamente, en cada fondo se reemplaza los residuos obtenidos en el paso anterior, con el objeto de crear una nueva muestra correspondiente a una pseudo serie de tiempo de residuos, con el fin de aplicar la técnica de bootstrap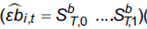
. El objetivo es estimar, 
(b=bootstrap), con muestras aleatorias para la generación de residuos. Con los residuos obtenidos se impone el tercer paso, que es construir una nueva pseudo serie de tiempo de rendimientos en exceso para el fondo, imponiendo como restricción la hipótesis nula de desempeño cero, o lo que es equivalente, alfa = 0. Por lo tanto la expresión resulta como se expone:
(11)
Como indica la ecuación 11, se está frente a una secuencia de rendimientos artificiales con alfas estadísticamente ciertos y cero por construcción. Por lo tanto, cuando nuevamente se regresa para una muestra b generada por el bootstrap sobre el modelo de Carhart, se puede obtener un valor positivo (negativo) de alfa y estadísticamente significativo, resultante del alto número de residuos positivos (negativos) que verifican la conducta de administradores con rendimientos extremos (asimétricos y con curtosis). Recursivamente, aplicado el procedimiento sobre los fondos evaluados (i) y reiteradas veces (b), se puede obtener un corte transversal de los alfas. Si de las iteraciones se llega a concluir que existen alfas positivos con valores significativos estadísticamente, en relación con aquellos observados en el modelo tradicional (ecuación 7), se puede concluir que los alfas extremadamente positivos no son sencillamente originados por las variaciones en la muestra. Por lo tanto, los alfas altos no son debido al azar, claramente existen habilidades en las estrategias implementadas por los administradores, que obtienen rendimientos en exceso más allá de los parámetros capturados por distribuciones normales.
Rendimientos condicionales y factores de descuento estocásticos: existe un conjunto de nuevos modelos, complejos desde el punto de vista matemático, cuyo objetivo es examinar las habilidades de los administradores de fondos durante los ciclos de negocio. Ferson y Schadt (1996) demuestran que los administradores de fondos no mantienen constante la exposición al riesgo, sino que se adaptan según la evolución de indicadores de negocios a través del tiempo. Christopherson, Ferson y Glassman (1998) hallaron evidencia empírica sobre las variaciones en los alfas condicionados a determinadas habilidades y herramientas empleadas por los administradores de fondos ante determinadas condiciones económicas. Las causas son varias, por ejemplo, las habilidades que los administradores van adoptando en el tiempo o empleo de determinadas estrategias durante un ciclo económico. Esto hace que los rendimientos y los alfas se condicionen a factores macroeconómicos. Es decir, ciertas circunstancias económicas condicionan las conductas de los administradores y por lo tanto los rendimientos esperados de los fondos. Moskowitz (2000) y Kosowski (2011) demuestran que, en promedio, los administradores con estrategias activas son más proclives a generar alfas positivos en épocas de recesión. Los modelos basados en los rendimientos condicionales son una derivación de los modelos lineales (Jagannathan y Wang, 1996), sin perjuicio de que exista evidencia a favor y en contra de los mismos (Lewellen y Nagel, 2006). La base consiste en asumir qué parámetros, como alfa y beta en CAPM, capturan y, por lo tanto, se comportan de manera dinámica según el nivel de factores macroeconómicos, por ejemplo las tasas de interés de corto plazo, el rendimiento de la cartera de mercado y otro conjunto de variables. Consecuentemente, las medidas para evaluar el desempeño (por ejemplo ratio de Sharpe o coeficiente alfa) no pueden mantenerse invariables en el tiempo, ajustándose en la explicación de rendimientos anormales a los factores macro que condicionan el resultado de los indicadores y el deber ser de un rendimiento normal.
Otra alternativa es trabajar con factores de descuento estocásticos (SDF, por las siglas en inglés de stochastic discount factors) como medida de evaluación de desempeño (Chen y Knez, 1996; Dahlquist y Soderlind, 1999; Ferson, Henry y Kisgen, 2006). En este campo los precursores son Grinblatt y Titman (1989b), quienes proponen estimar rendimientos a partir de la variación en el tiempo de la utilidad marginal del inversor. Basados en la ley del precio único, debe existir un SDF ( mt ) que valúe los rendimientos esperados de una cartera pasiva, no condicionada a ningún tipo de información, generando un resultado de alfa igual a cero.
(12)
También, los rendimientos esperados generados por estrategias condicionadas a la existencia de información pública al final del periodo anterior ( zt-1 ) generan un resultado de alfa igual a cero.
(13)
A partir de un conjunto de restricciones establecidas, la estimación de SDF se realiza con el método generalizado de momentos6. Las mencionadas restricciones impuestas son las condiciones de momento empleadas en la estimación del SDF, permitiendo al investigador evitar seleccionar apriorísticamente una distribución de probabilidad para carteras activas y pasivas. Estimado el SDF, este sirve para valuar carteras con gestión activa, durante el intervalo de tiempo seleccionado y consecuentemente ponderar el desempeño comparando rendimientos observados con aquellos teóricos estimados a partir del SDF, mediante el alfa.
(14)
En este sentido, el mejor desempeño se encuentra asociado a mayores alfas, obtenidos de los rendimientos en exceso por estrategias activas, cuyo benchmark es el SDF.
2.4. Análisis basados en las tenencias o estructuras de carteras de FCI
En un nivel más específico se encuentran los métodos que analizan el desempeño de los fondos, concentrándose no solamente en los rendimientos, sino también en las tenencias y clases de activos. Bajo este grupo se engloban los estudios conocidos con el nombre de análisis de desempeño basado en tenencias. Las ventajas del método son: a) estudiar las estructuras de inversiones y dinámica del fondo permite elaborar comparables específicos; b) analizar el rebalanceo de inversiones al detalle y permitir calificar; c) evitar la interferencia de los costos de transacción al estudiar inversiones y asignación de fondos antes de computar tales gastos7; d) desagregar el verdadero valor añadido de la estrategia activa, e) el benchmark es más preciso debido a que se construye el comparable en función de las características de los activos que integran el fondo, dejando de ser una cartera de mercado o simple índice macro. A continuación se resumen los dos métodos clásicos empleados en el estudio de composición de fondos.
El método de la autoevaluación (Self-Benchmarking Method of Performance Evaluation): bajo esta denominación se conoce al método desarrollado por los trabajos iniciales de Grinblatt y Titman (1989a) quienes emplearon datos de carteras de fondos publicados por la Security Exchange Commission. Los datos fueron estudiados a nivel de tenencias y composición de carteras. Los autores, a partir de los rendimientos observados en función de las tenencias, desarrollaron lo que denominaron desempeños hipotéticos de administradores con base en patrones de tenencias. Para elaborar medidas de desempeño, regresaron los rendimientos hipotéticos con base en las estrategias planteadas contra comparables seleccionados, con el fin de obtener los alfas correspondientes a los desempeños hipotéticos según la composición de la cartera y evolución de la misma.
Evaluación con base en las características de la cartera: Daniel, Grinblatt, Titman y Wermers (1997) utilizan los resultados de estudios empíricos (Roll y Ross, 1980; Fama y French, 1992, 1993, 1996; Jegadeesh y Titman, 1993) para explicar los factores que determinan el rendimiento de las acciones y con ellos evaluar el desempeño en función a las características que presenta la composición de los fondos de acciones y bonos. Kothari y Warner (2001) manifiestan que este método permite evaluar el fondo, presentando una mayor habilidad para detectar rendimientos anormales que el modelo de Carhart (1997), en particular, si el estilo o características del fondo difieren de la tradicional composición de los índices de mercado. Asimismo, este método incorpora al análisis el volumen de negociación y fondos aplicados, inferidos de los cambios en la composición de la cartera a través del tiempo, mejorando el diagnóstico relativo al desempeño del administrador de cartera.
3. Índice multifactorial para el análisis del desempeño
En el anterior apartado fueron expuestos diferentes modelos y metodologías para evaluar el desempeño de los activos financieros. Conforme fue expresado, el objetivo del presente trabajo consiste en elaborar y testear un índice multifactorial destinado a evaluar el desempeño financiero de fondos comunes de inversión. El modelo propuesto analiza el desempeño de los fondos, añadiendo a la dimensión rendimiento y riesgo, variables tales como diversificación, liquidez, tamaño, riesgo financiero, eficiencia y costos de transacción. Estos factores están relacionados con aspectos que se consideran clave en este tipo de inversiones, como la liquidez, y vinculados a atributos deseables a partir de los modelos y métricas presentados anteriormente, como la diversificación de la cartera.
Con esta propuesta multifactorial se pretende analizar la solidez del fondo, incorporando variables que atañen a su integración estructural, complementando el clásico estudio de las dimensiones rendimiento y riesgo. El presente índice puede ubicarse como un híbrido entre los modelos que analizan desempeño con base en rendimientos y aquellos que analizan las composiciones estructurales de los activos financieros objeto de estudio. Esta aseveración encuentra fundamento en las variables incorporadas en el análisis, como el grado de diversificación, el tamaño y la liquidez. Estas se refieren a la estructura y composición de los fondos. En efecto, el índice se encuentra compuesto por nueve variables que se detallan en la subsección 3.1 y abarcan aspectos relacionados con la eficiencia, diversificación, liquidez, tamaño, riesgo financiero y honorarios.
3.1. Múltiples dimensiones para medir el desempeño: las variables del índice
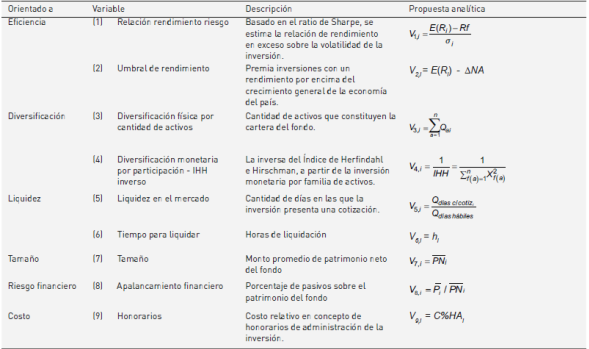
A continuación se describe cada factor propuesto, exponiendo su expresión analítica y las variables operativas seleccionadas para realizar la correspondiente medición.
a) Relación rendimiento riesgo: la presente relación es capturada a través de una medida de eficiencia relativa, basada en el ratio de Sharpe. Se estima para cada clase de fondo la relación de rendimiento en exceso sobre la volatilidad de la inversión. Como rendimiento de la cartera E( Ri ) se toma el rendimiento aritmético diario sobre la cotización de la cuota-parte del fondo y se procede a anualizarlo, multiplicándolo por la cantidad de días hábiles del periodo bajo análisis. Como proxy de la tasa de rendimiento de un activo libre de riesgo Rf se toma la tasa interna de retorno (TIR) de un título soberano emitido en moneda local. Finalmente, para medir la volatilidad σi se trabaja con el desvío estándar anualizado de los rendimientos aritméticos diarios del fondo, multiplicándolo por la raíz cuadrada de la cantidad de días hábiles del periodo. De este modo, la variable V1,i se estima como se presenta a continuación:
(15)
b) Umbral de rendimiento: esta variable pretende premiar aquellas carteras de inversiones que presenten un rendimiento por encima del crecimiento general de la economía del país. La misma es calculada como la diferencia entre el rendimiento anual aritmético del fondo menos el crecimiento o variación de alguna variable macroeconómica que referencie el nivel de actividad (NA). En este caso las alternativas disponibles para el caso de Argentina, utilizando fuentes oficiales, son el crecimiento del producto bruto interno (PBI) durante el período bajo análisis o la variación acumulada de una medida conocida como estimador mensual de actividad económica (EMAE). Se testean alternativamente las dos medidas, escogiéndose trabajar con la variación del EMAE por tener una periodicidad mensual versus la frecuencia trimestral que posee el PBI. La variable V2,i tiene un efecto positivo sobre el índice en cuestión en el caso de aquellos fondos que presenten un rendimiento por encima del umbral, y a la inversa un efecto negativo para las carteras cuyo rendimiento esté por debajo del promedio de actividad económica del país. La expresión formal de la variable V2,i es la siguiente:
(16)
c) Diversificación física por clase de activos: se pretende medir el grado de diversificación del fondo a partir del número de activos que lo componen. La medida es calculada como la sumatoria de la cantidad de activos empleados por el fondo, con participación estrictamente positiva en la cartera durante el período bajo análisis, como se indica en la siguiente expresión:
(17)
Siendo ai los activos que componen la cartera del fondo i, por lo que la sumatoria física de cantidad de activos (Q) se restringe a aquellos con participación estrictamente positiva dentro de la cartera durante el período bajo análisis, esto es con Xa,i > 0.
d) Índice Herfindahl e Hirschman inverso: como complemento de la métrica anterior, se propone una variable que mida la diversificación monetaria a través de la inversa del índice de Herfindahl e Hirschman (IHH)8. El IHH es utilizado habitualmente para medir concentración empresarial en un mercado y en tal sentido, el aporte del presente trabajo consiste en emplear la medida de los cuadrados de las participaciones de las empresas en un mercado. La medida se adaptó para medir la concentración de familias de activos en la cartera, al elevar las participaciones de las familias de activos al cuadrado y sumarlas. Las participaciones en este caso se calculan sobre valores monetarios totales invertidos por el fondo en esa familia de activos sobre el patrimonio total de la cartera en ese plazo, para luego ser expresados en tanto por uno.
(18)
Donde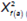 
representa la participación en la cartera del fondo correspondiente a la familia de activos f(a), elevada al cuadrado.
e) Liquidez en el mercado: la variable propuesta como liquidez en el mercado cuantifica, en términos relativos, la cantidad de días en los que la inversión presenta una cotización en el mercado. Sirve para castigar aquellos fondos con un número reducido o nulo de cotizaciones durante todo el periodo bajo análisis, pretendiendo que en el ranking se posicionen mejor los fondos que participaron activamente durante todo el período, es decir aquellos con mercado secundario desarrollado y bajo riesgo de liquidez. La expresión formal de la variable es:
(19)
Siendo 
la cantidad de días en el período donde el fondo presenta cotización en el mercado.
f) Tiempo para liquidar: la siguiente variable es complemento de la anterior, al buscar incorporar una métrica vinculada a la facilidad para deshacerse de la inversión a través de las horas de liquidación del fondo. Dado que a mayor cantidad de horas menor liquidez, la variable V6,i incide negativamente sobre el valor del índice.
(20)
Donde hi son las horas de liquidación del fondo i.
g) Tamaño: el tamaño del fondo está vinculado al valor en unidades monetarias del patrimonio neto promedio de la cartera de inversión durante el período bajo análisis. A mayor tamaño se espera que el fondo sea menos riesgoso, por lo tanto guarda una relación positiva respecto al índice de desempeño financiero.
(21)
Donde 
es el patrimonio neto promedio del fondo i.
h) Apalancamiento financiero: medida de endeudamiento a partir del ratio del pasivo promedio del fondo 
sobre el patrimonio neto del fondo i (). Fondos más apalancados presentan mayor nivel de riesgo financiero, por lo tanto incide negativamente sobre el índice de desempeño financiero.
(22)
i) Honorarios: la última variable incluye el costo del fondo en concepto de honorarios de administración de la inversión. Mayores costos inciden de manera negativa en el valor del índice de desempeño financiero.
(23)
Siendo C%HAi el costo porcentual en concepto de honorarios de administración del fondo i.
A modo de síntesis, la tabla 1 resume los conceptos desarrollados anteriormente, agrupando las variables en función de las dimensiones que se pretenden medir como eficiencia, diversificación, liquidez, tamaño, riesgo financiero y costos.
3.2. El índice multifactorial para evaluar desempeño
Considerando las nueve variables anteriormente mencionadas, el índice ( Ii ) se constituye como una suma algebraica en la que cada métrica está normalizada (ecuación 24). Para este proceso de normalización, en el numerador del índice el valor correspondiente a la variable x para el fondo i ( Vx,i ), se procede a dividirlo por el máximo valor observado para la variable x, este último obtenido de considerar todos los fondos de la muestra objeto de estudio. Por lo tanto, el índice se construye agregando en el numerador las nueve variables normalizadas, suma algebraica situada en el numerador del índice. En el denominador del índice, y a los efectos de escalar e interpretar el resultado de desempeño financiero en un intervalo de valores de situado en el intervalo [-1,1], se divide por el máximo valor de desempeño observado en el mercado. Es decir, el denominador del índice, notado como A, se calcula como el máximo de los numeradores para el universo de fondos (ecuación 25).
(24)
Donde
(25)
El resultado obtenido aplicando la ecuación 24 en cada fondo evaluado permite elaborar un ranking de acuerdo a su desempeño evaluado de manera multidimensional. Aquellos fondos con índices más próximos a la unidad serán los de mejor comportamiento conjunto para las nueve métricas consideradas de interés.
4. Implementación del índice multifactorial de desempeño financiero: análisis de los fondos comunes de inversión en el mercado de capitales argentino
Para ilustrar y validar la metodología propuesta se utiliza el método de análisis de casos (Castro, 2010), bajo un enfoque cuantitativo. El alcance de la investigación es descriptivo-correlacional y el diseño es no experimental y transversal. Para ello, el índice desarrollado en la ecuación 24 se utiliza para elaborar un ranking de desempeño durante el periodo 2016, tomando como unidad de análisis los fondos comunes abiertos negociados en el mercado de capitales argentino. La elección del año en cuestión se justifica por varias causas, a saber: la impulsión del mercado financiero argentino producto de un cambio de gobierno en el país a fines del año 2015, el crecimiento de la inversión en fondos, la actualidad de los datos y un período relativamente breve para no distorsionar las cifras calculadas producto del proceso inflacionario acontecido.
En Argentina, los fondos se pueden clasificar por tipo en: (1) Renta variable: en estos se invierte, principalmente, en acciones del mercado doméstico e internacional, a través de inversiones directas o certificados de depósitos argentinos. La cuotaparte se expresa en dólares o moneda de curso legal. (2) Renta fija: estos fondos invierten, mayoritariamente, en títulos de deuda pública o privada, nacionales o extranjeros. Igual que en el caso anterior, la cuotaparte está denominada en dólares o moneda doméstica. (3) Renta mixta: se trata de inversiones combinadas en acciones y títulos de deuda como los descritos en los casos anteriores, con similares características al fondo de renta fija. (4) Mercado de dinero: en esta categoría se incorporan los fondos de plazo fijo y los de mercado de dinero, los que tienen similar comportamiento aunque se diferencian por su marco regulatorio. Ambos construyen sus carteras con depósitos en entidades financieras (depósitos a plazo fijo y colocaciones a la vista en entidades financieras). Según la Resolución General 622 (2013) de la Comisión Nacional de Valores, tienen como restricción la obligación de ''mantener en todo momento, al menos, un 45% del patrimonio del fondo en colocaciones totalmente líquidas. La cuotaparte está denominada en moneda doméstica o en dólares''. Las colocaciones se circunscriben solamente a entidades financieras nacionales con un horizonte de vencimiento de corto plazo. (5) PyMEs: este tipo de fondo está orientado a instrumentos destinados al financiamiento de las pequeñas y medianas empresas (PyMEs). Su objetivo es alentar el desarrollo de las distintas industrias mediante la administración de una cartera de inversiones constituida de instrumentos financieros y valores negociables, de renta fija y variable, emitidos por este tipo de empresas, incluyendo acciones PyMEs, cheques de pago diferido, pagarés bursátiles, obligaciones negociables para PyMEs, valores de corto plazo, fideicomisos financieros, entre otros. Podrían ser considerados como una especie dentro del tipo de renta mixta, dada la posibilidad que tienen de componer su cartera con instrumentos de renta fija y variable, pero al igual que para el resto de tipos, se consideran una categoría mutuamente excluyente a los fines del trabajo. No obstante, producto de la limitada oferta de acciones PyMEs que presenta el mercado de capitales local, suelen alocar mayoritariamente su patrimonio en activos de renta fija. Según la Resolución General 622 (2013) de la Comisión Nacional de Valores, ''el 75%, como mínimo, del haber de este tipo de fondos deberá invertirse en valores negociables emitidos por PyMEs y/o emitidos por otras entidades cuya emisión tenga como objetivo o finalidad el financiamiento de PyMEs''. (6) Infraestructura: son aquellos que buscan obtener una rentabilidad, principalmente, a través de la inversión en instrumentos de renta fija y variable, emitidos tanto por el sector público como privado, dedicados a financiar, invertir o desarrollar proyectos de infraestructura y transporte y emprendimientos productivos que impulsen el desarrollo de las economías regionales en la Argentina. También podrían ser contemplados como una especie dentro del segmento de renta mixta. De acuerdo a la Resolución General 622 (2013) de la Comisión Nacional de Valores, ''el 75%, como mínimo, del haber de este tipo de fondos deberá invertirse en activos que compongan el objeto especial de inversión antes señalado''. (7) Retorno total (total return): son aquellos cuyo principal objeto es generar un alto nivel de valorización del capital a través de la inversión de su patrimonio indistintamente en activos de renta variable y/o de renta fija, públicos o privados, ambos con oferta pública, y en otros fondos comunes de inversión. La característica principal radica en que, si bien ajustan sus tenencias dentro de los límites máximos y mínimos que establecen sus reglamentos de gestión, poseen una mayor flexibilidad en la asignación estratégica y táctica de sus activos. Asimismo, estos fondos pueden ser diferenciados de aquellos denominados de retorno absoluto (absolute return), puesto que, mientras que los primeros participan de la evolución general de los mercados, los segundos, con igual flexibilidad, tratan de eliminar cualquier relación con los mercados. A diferencia de los productos tradicionales de gestión activa, Molaguero (2016, p. 24) indica que ''los fondos de retorno total se gestionan sin compararse frente a ningún índice de referencia. La filosofía que subyace es que gestionar contra un índice de referencia puede aportar ventajas comerciales pero no añade nada en cuanto a rentabilidad''. Este tipo de fondos puede ser considerado como una categoría dentro de los de renta mixta.
Por otra parte, es importante aclarar que, independientemente de las posibles clasificaciones y las diversas estrategias de composición de cartera (Pesce, Milanesi, Redondo, El Alabi, Amarilla, 2016), los fondos comunes de inversión en Argentina se encuentran sujetos a una importante restricción, reconocida en el artículo 6 de la Ley N° 24.083 (1992), el cual establece que ''en el caso que el haber del fondo consista en valores mobiliarios, estos deben contar con oferta pública en el país o en el extranjero debiendo invertirse como mínimo un 75 % en activos emitidos y negociados en el país''.
Para el estudio se toman como fuentes de datos secundarios las bases provistas por la consultora Economatica® e información complementaria del Instituto Nacional de Estadística y Censos (INDEC) de la República Argentina. La primera fuente de datos la constituyen las cotizaciones diarias, correspondientes a las cuotapartes de los 426 fondos comunes negociados en Argentina durante el período comprendido entre el 01/01/2016 y el 31/12/2016. No se debe perder de vista que las cuotapartes cotizan por clase de fondo. Un mismo tipo de fondo puede tener diferentes clases dependiendo del perfil de los inversores (institucionales o individuales), montos de inversión mínimos, costos de transacción, duración del fondo, etc. A pesar de que la cartera administrada será la misma, las distintas clases buscan generar un producto que se adapte a las necesidades específicas de cada segmento de inversores. De esta manera, con una misma cartera es posible capturar el capital de inversores institucionales y del mercado minorista. Los primeros deben suscribir un capital mínimo mayor, que se traduce en economías de escala para el administrador del fondo y se materializan en menores comisiones de gestión que las abonadas por el inversor minorista. Si bien los objetivos de inversión pueden ser similares, las escalas y necesidades pueden diferir entre distintos tipos de inversores, las distintas clases de un mismo fondo pretenden abarcar dichas particularidades. En cada clase, con numeración internacional de identificación de valores diferente (ISIN, por la sigla en inglés de International Securities Identification Numbering System), los fondos pueden designarse con diferentes letras (A, B, C, I, etc.), respondiendo a la misma categoría, según sean de acumulación o reparto, y dentro de estas, institucionales, minoristas, en moneda extranjera, etc. Cabe destacar que la forma de denominar a las clases no está generalizada, dependiendo de la sociedad gerente.
Consecuentemente se desagregan los fondos por clase para su análisis, arrojando un total de 969 clases en el mercado de Argentina para el período seleccionado. Sobre esta información, son calculados los parámetros para cada clase de fondo, relativos a las variables de la tabla 1, a saber: (1) relación rendimiento riesgo (ratio de Sharpe), (2) umbral de rendimiento y (5) liquidez en el mercado.
La variable rendimiento riesgo (1) o ratio de Sharpe es calculada considerando como tasa libre de riesgo el rendimiento anual promedio de las Letras en pesos del Banco Central de la República Argentina (LEBAC) a un plazo de 252 días.
En relación con la variable (2) son utilizados los datos del INDEC9, tomando la diferencia entre el rendimiento anual por clase de fondo y la variación del EMAE, indicador macroeconómico de actividad seleccionado como proxy de dicha variable.
Al estimar el ratio de liquidez (5) se consideran como días hábiles de cotización los días laborales en función al calendario publicado por el diario La Nación10, observando un total de 247 días al año.
Asimismo se utiliza la información de la composición de las carteras de cada fondo, provista por Economatica® durante el período bajo análisis para estimar los valores correspondientes a las variables de la tabla 1: (3) diversificación física por cantidad de activos, (4) diversificación monetaria por participación - IHH inverso, (7) tamaño y (8) apalancamiento financiero.
Finalmente, se utilizan los datos generales de los fondos comunes con el fin de asignar valor a los atributos de: (6) tiempo para liquidar y (9) honorarios de administración.
Lo anteriormente descrito permite estimar un índice de desempeño financiero para cada clase de fondo, teniendo en cuenta que las variables (1), (2), (5) y (9) pueden presentar diferentes valores para un mismo fondo común. Este es así debido a que cada clase presenta su cotización en el mercado y por lo tanto genera un determinado rendimiento.
5. Resultados
A continuación se exponen los principales resultados obtenidos de manera deductiva, analizando resultados generales y específicos por clases de fondos.
5.1. Resultados del análisis general
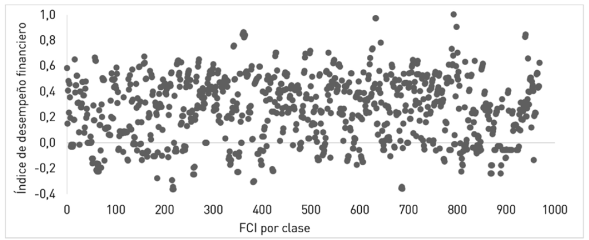
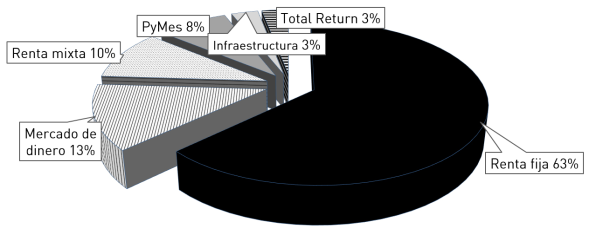
La figura 3 presenta la dispersión de valores correspondiente a todo el mercado de fondos comunes argentino, periodo 2016, producto de aplicar el índice contenido en la ecuación 24. Conforme se puede apreciar, la mayoría de los fondos tuvo un índice mayor a cero. En este grupo la mayor concentración se encuentra en el intervalo [0; 0,6]. Si se analizan los 100 primeros fondos por clase, ordenados a partir del índice de desempeño financiero, aquellos con mejor desempeño son en promedio de renta fija, seguidos por mercado de dinero y renta mixta, conforme se expresa en la figura 4. De ellos, el 92% cotiza originalmente en pesos argentinos y el 8% restante en dólares americanos.
Fuente: elaboración propia.
Figura 3 Dispersión de valores para el índice de desempeño financiero sobre fondos comunes de inversión argentinos
Producto de aplicar el índice propuesto al caso de estudio, la tabla 2 presenta las primeras 40 posiciones de fondos comunes, en función del desempeño observado para el periodo 2016. Las 15 primeras posiciones son ocupadas por fondos del tipo infraestructura, mercado de dinero y renta fija.
5.2. Ranking por tipo de fondos
En esta subsección se presenta el resumen de los resultados obtenidos aplicando el índice sobre los diferentes tipos de fondos. Para facilitar la interpretación de los resultados arrojados en este estudio descriptivo, en la tabla 3 se presenta una serie de estadísticos descriptivos tomando en cuenta los valores estimados de la medida propuesta para evaluar el desempeño de todas las clases por tipo de fondo, con el fin de sistematizar y sintetizar la información arrojada por el índice, expuesta por cada tipo de fondos en los anexos (tablas A1, A2, A3, A4, A5, A6, A7).
Tabla 2 Ranking general de FCI en Argentina - año 2016
| Denominación del fondo | Código | Í (ec.24) | Tipo de fondo |
|---|---|---|---|
| Schroder Infraestructura | 826 | 1,00000 | Infraestructura |
| Pellegrini Renta Pesos | 631 | 0,97253 | Mercado de dinero |
| Pellegrini Renta Pesos | 120 | 0,97076 | Mercado de dinero |
| Schroder Renta Fija | 829 | 0,90249 | Renta fija |
| Fima Ahorro Pesos | 735 | 0,86128 | Renta fija |
| Fima Ahorro Pesos | 193 | 0,85033 | Renta fija |
| Supergestion Mix Vi | 731 | 0,84351 | Renta fija |
| Fima Ahorro Pesos | 734 | 0,84298 | Renta fija |
| Fima Ahorro Plus | 1010 | 0,83895 | Renta fija |
| Fima Ahorro Plus | 1009 | 0,82804 | Renta fija |
| Supergestion Mix Vi | 730 | 0,82516 | Renta fija |
| Fima Ahorro Plus | 1008 | 0,82073 | Renta fija |
| Pionero Renta Ahorro | 727 | 0,77887 | Renta fija |
| Fba Ahorro Pesos | 895 | 0,75679 | Renta fija |
| Fba Ahorro Pesos | 287 | 0,74948 | Renta fija |
| Pellegrini Renta Fija | 633 | 0,73455 | Renta fija |
| Schroder Corto Plazo | 285 | 0,73328 | Renta fija |
| Pellegrini Renta Fija | 271 | 0,72745 | Renta fija |
| Iam Ahorro Pesos | 1293 | 0,71766 | Mercado de dinero |
| Schroder Renta Global Fci | 966 | 0,70250 | Renta mixta |
| Lombard Capital | 786 | 0,70144 | Renta fija |
| Galileo Event Driven | 965 | 0,70093 | Total Return |
| Galileo Event Driven | 583 | 0,70093 | Total Return |
| Iam Ahorro Pesos | 1292 | 0,69913 | Mercado de dinero |
| Hf Pesos Plus | 711 | 0,69502 | Renta fija |
| Schroder Infraestructura | 600 | 0,68059 | Infraestructura |
| Galileo Event Driven | 582 | 0,67443 | Total Return |
| Axis Renta Fija | 1110 | 0,67179 | Renta fija |
| Alpha Ahorro | 73 | 0,66399 | Renta fija |
| Hf Pesos Plus | 712 | 0,66288 | Renta fija |
| Pellegrini Empresas Argentinas Pymes | 961 | 0,66215 | PyMes |
| Tavelli Global | 1057 | 0,65598 | Renta mixta |
| Consultatio Ahorro Plus Argentina F.C.I. | 1035 | 0,65097 | Renta fija |
| Al Abierto Pymes | 874 | 0,64989 | PyMes |
| Maf Pesos Plus | 1020 | 0,64740 | Renta fija |
| Rj Delta Ahorro Plus | 932 | 0,64633 | Renta fija |
| Cohen Renta Fija | 1044 | 0,64374 | Renta fija |
| Alpha Ahorro | 699 | 0,64212 | Renta fija |
| St Renta Plus | 1082 | 0,63916 | Renta fija |
| Cohen Renta Fija | 1043 | 0,63806 | Renta fija |
Fuente: elaboración propia con datos provistos por Economatica ®.
La tabla 3 aporta, a través de los estadísticos descriptivos, una síntesis del desempeño de las clases. Conforme se puede apreciar, el mejor desempeño promedio para el periodo 2016 fue alcanzado por los fondos de mercado de dinero, seguidos por la clase total return. Estas clases de fondos, además de evidenciar un resultado promedio superior al resto del índice, presentan en conjunto un comportamiento más estable, producto de la baja dispersión en el resultado del indicador, interpretado también a través del coeficiente de variación. En el extremo opuesto se encuentran los fondos de renta variable, renta mixta e infraestructura, ordenamiento que surge en función del coeficiente de variación del índice. Esto pone de manifiesto la utilidad del índice, ya que trabajando en una sola dimensión como el rendimiento-riesgo, las conclusiones hubiesen sido opuestas. En este caso, el índice mide el comportamiento integral del fondo evaluando su solidez estructural, a través de variables complementarias al riesgo y el rendimiento, incorporando la liquidez, diversificación y costos de transacción.
Tabla 3 Resumen de resultados correspondiente al índice año 2016
| Clase | Promedio | Dispersión | Máximo | Mínimo | Coeficiente de variación |
|---|---|---|---|---|---|
| Renta fija | 0,28445 | 0,26370 | 0,90249 | -0,36464 | 0,92706 |
| Mercado de dinero | 0,48765 | 0,14485 | 0,97253 | 0,16410 | 0,29704 |
| Renta mixta | 0,18434 | 0,22557 | 0,70250 | -0,24855 | 1,22366 |
| PyMEs | 0,30918 | 0,25245 | 0,66215 | -0,22502 | 0,81651 |
| Total return | 0,41634 | 0,19040 | 0,70093 | 0,01266 | 0,45733 |
| Infraestructura | 0,24380 | 0,27142 | 1,00000 | -0,13638 | 1,11328 |
| Renta variable | 0,13769 | 0,16930 | 0,40154 | -0,27971 | 1,22955 |
Fuente: elaboración propia con datos provistos por Economatica ®.
6. Conclusiones
A menudo los activos financieros son analizados solamente desde la perspectiva del rendimiento o riesgo, sin abordar otros aspectos que determinan su desempeño. Realizar un diagnóstico financiero integral de un fondo implica incorporar variables que expliquen múltiples dimensiones relativas al desempeño que el activo financiero pueda proyectar en el mediano y largo plazo. La medida, sencilla y práctica, se posiciona en el universo de métodos basados en el estudio de rendimientos. Su fuente de información está integrada por un conjunto de datos objetivos de mercado, capturados a partir de indicadores que miden y escalan dimensiones múltiples relativas al desempeño de las carteras. El índice en cuestión incorpora variables que lo hacen novedoso, como la inversa del índice de Herfindahl e Hirschman, complementaria a la medida de diversificación física, el grado de apalancamiento financiero de los fondos y los honorarios percibidos por los administradores. Los resultados que arroja el índice son descriptivos y sintéticos relativos a las dimensiones evaluadas, devengando un criterio de ordenamiento multidimensional.
Para estudiar e ilustrar su funcionamiento se utilizó el método de análisis de casos. Para ello se trabajó con el universo de fondos cotizantes en el mercado de capitales argentino durante el periodo 2016. Los resultados obtenidos permitieron ordenar a los 100 fondos de mejor desempeño. Considerado individualmente, el fondo de mejor desempeño corresponde a la clase infraestructura. Agrupados por tipos de fondos y en función de los resultados arrojados por los estadísticos descriptivos, los mejores desempeños promedios se asocian con fondos del mercado de dinero y total return. Por otro lado, fondos como infraestructura, renta mixta y renta variable en su conjunto presentan altos niveles de dispersión normalizada de acuerdo al valor promedio del índice de desempeño (coeficiente de variación), por lo que su grado de volatilidad no fue compensado por el desempeño financiero del tipo de fondo. De esta forma, se pone de manifiesto que el estudio de una dimensión única, como el rendimiento-riesgo, pueden conducir a conclusiones divergentes, a diferencia de un estudio integral, el cual apunta a evaluar la solidez del desempeño, tomando en cuenta la diversificación, liquidez, costos transaccionales, umbrales de rendimiento, tamaño y apalancamiento financiero.