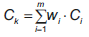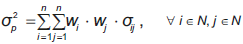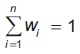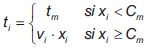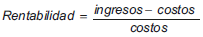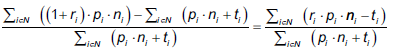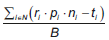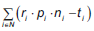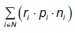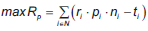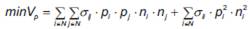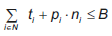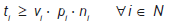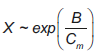1. Introducción
En la administración y evaluación financiera de proyectos es posible encontrar situaciones en las cuales se presentan flujos de caja no convencionales, que de acuerdo con Baca Currea (2004), se obtienen cuando los ingresos y los egresos se encuentran alternados en el tiempo. Esta situación permite la posibilidad de reinversiones en caso de exceso de liquidez. Sin embargo, además de generar una ganancia adicional, dicha reinversión debería entregar sus retornos cuando los flujos de caja así lo requieran. Por lo tanto, de acuerdo al presupuesto, riesgo y costo de capital del proyecto, el gerente de proyectos se enfrenta a una serie de decisiones en esta situación.
En el siguiente ejemplo, tomado de Gómez y Benjumea (2011) , se contrastan dos posibles alternativas: i) no reinvertir y asumir los costos de oportunidad del exceso de liquidez; o ii) reinvertir los dineros disponibles sin afectar el cronograma planteado por el flujo de caja del proyecto:
''Un proyecto requiere una inversión inicial de 80.000 dólares. En el primer periodo los ingresos son iguales a los egresos, en el segundo periodo hay un ingreso neto de 200.000 dólares, en el tercer y cuarto periodo los ingresos y los egresos vuelven a dar un flujo de caja neto de cero, finalmente en el quinto periodo hay un egreso de 120.000 dólares. Suponiendo una tasa de financiación del 25% y la no reinversión del dinero en los diferentes periodos, se obtiene una Tasa Interna de Retorno Modificada (TIRM) del 10,9%. Sin embargo, si se considera la posibilidad de reinvertir el dinero a una tasa del 30% o del 8%, la TIRM que resulta es del 29% y del 16%, respectivamente'' (Gómez y Benjumea, 2011, p. 79).
Lo que se pretende mostrar en el ejemplo anterior es que la reinversión en proyectos con flujos de caja no convencionales puede traer consigo resultados positivos para el proyecto, los cuales están en función de la tasa de reinversión que se obtenga. Por lo tanto, es de interés para el gerente de proyectos conocer alternativas que le permitan aumentar la rentabilidad. Adicionalmente, el riesgo es otro factor de importancia al evaluar las diferentes alternativas. Incluso, el grado de aversión al riesgo puede variar durante la ejecución del proyecto. Por ejemplo, una exposición al riesgo durante cuatro periodos y comprometiendo capital que puede ser requerido en periodos intermedios es menos deseable que asumir riesgos similares en los últimos periodos de la ejecución del proyecto.
Durante los últimos años, el Valor Presente Neto (VPN) y la Tasa Interna de Retorno (TIR) han sido herramientas útiles para la evaluación financiera de inversiones en la gestión de proyectos. Sin embargo, a pesar de su popularidad, Kierulff (2008) muestra que ni el VPN ni la TIR están diseñadas para abordar muchas de las situaciones que se encuentran en la realidad, especialmente aquellas relacionadas con flujos de caja intermedios invertidos a una tasa diferente a la tasa de retorno del proyecto.
Estos flujos de caja adicionales pueden resultar de un exceso de liquidez que, de no ser invertidos apropiadamente, podrían convertirse en un costo de oportunidad constituido principalmente por el costo relativo a las fuentes de financiación del proyecto. Para calcular este costo se utiliza normalmente el costo promedio ponderado de capital o WACC (Weighted Average Cost of Capital) (Baker y Powell, 2009) expresado en la ecuación:
Donde C k es el costo promedio ponderado de capital o WACC, w i es la participación de la fuente i, C i es el costo de financiación de la fuente i después de impuestos y m es el número de fuentes de financiación. Para el problema abordado, el WACC resulta importante porque representa el costo de oportunidad que tiene el proyecto, el cual puede evitarse si se decide reinvertir el exceso de liquidez producto de los flujos de caja no convencionales. El WACC, a pesar de haber recibido algunas críticas en la literatura (Miller, 2009a, 2009b), sigue siendo una buena forma calcular el costo de las fuentes de financiación (Bade, 2009; Pierru, 2009a, 2009b).
No obstante, este exceso de liquidez puede ser reinvertido a una tasa diferente a la TIR del proyecto como propone Baldwin (1959). En este caso se utiliza la Tasa Interna de Retorno Modificada (TIRM) con el fin de calcular la rentabilidad esperada del inversionista. Dicha reinversión lleva asociado un riesgo que depende del perfil del inversionista y también de un plazo que está determinado por los flujos de caja del proyecto.
Así, los mercados financieros se convierten en una opción atractiva para disminuir o eliminar los costos de oportunidad, del mismo modo que algunos autores proponen el mercado financiero como cobertura para la inflación (Arnold y Auer, 2015).
En 2013, Eugene Fama, Lars Peter Hansen y Robert Shiller obtienen el Nobel de Economía por sus estudios del comportamiento de los mercados bursátiles desde diferentes posiciones de pensamiento (Suárez, Duarte y Ortíz, 2015). Esto demuestra la vigencia e importancia que despierta la investigación de los mercados financieros. A la hora de invertir en este tipo de mercados, un inversionista tiene dos alternativas: renta fija y renta variable. La renta fija se refiere a depósitos de corto o largo plazo que generan un interés fijo, mientras que la renta variable está asociada a la variación de los precios que pueden tener los títulos de compañías, materias primas, divisas, entre otros. Esta última tiene un mayor riesgo asociado, lo que generalmente tiene asociado una alta rentabilidad.
El problema de elegir un portafolio puede ser analizado desde diferentes perspectivas. El análisis técnico por ejemplo estudia los patrones del mercado, incluyendo los comportamientos de la demanda y la oferta de las acciones (Achelis, 2000). Para lograr esto, se grafican los datos históricos y se analizan indicadores técnicos, dentro de los que se destacan las medias móviles, las bandas de Bollinger, el momentum, entre otros. Por otro lado, el análisis fundamental, planteado inicialmente por Graham y Dodd (1934), estudia la información financiera de las industrias de un sector con el fin de descubrir si el precio que refleja el valor de la compañía está infravalorado o sobrevalorado en el mercado. Finalmente, se encuentra la teoría de portafolios introducida por Markowitz (1952), en donde se responde la pregunta: ¿cómo se deben distribuir las inversiones dentro de las posibilidades existentes? Aquí, mediante un modelo de optimización, se pretende decidir la proporción del presupuesto disponible que se debe invertir en cada tipo de activo para conformar un portafolio de manera que se maximice la rentabilidad y se minimice el riesgo. En su modelo, Markowitz cuantifica la rentabilidad y el riesgo de un activo, usando medidas estadísticas de su retorno esperado y la desviación estándar. Este problema se conoce como media-varianza. Dado un conjunto N = {1,2,...n} de n acciones disponibles para invertir, matemáticamente la varianza y la rentabilidad se pueden expresar de acuerdo con las ecuaciones (2) y (3), respectivamente.
En (2) el parámetro σ ij representa la covarianza entre los rendimientos de los activos i y j, σ 2 p corresponde a la varianza del portafolio, n denota el número de activos disponibles y, w i y w j indican la proporción del portafolio a invertir en los activos i y j, respectivamente.
Similarmente, en (3) ri y rp son las rentabilidades esperadas del activo i y del portafolio p, respectivamente.
Las restricciones se muestran en las ecuaciones (4) y (5), las cuales indican que se debe invertir el total del capital disponible y que ninguna inversión puede ser negativa.
A pesar de la simplicidad y del planteamiento intuitivo del modelo de Markowitz, pasaron muchos años para que la optimización de portafolios fuera utilizada con dinero real (Kolm, Tütüncü y Fabozzi, 2014). En un principio, por ejemplo, no se consideraban los costos de transacción en la conformación del portafolio; esto hacía que frecuentemente las soluciones encontradas incurrieran en altos costos de este tipo y dejaran de ser soluciones eficientes (Yoshimoto, 1996). Al incorporar los costos de transacción en el modelo, la complejidad del problema aumenta, especialmente en un entorno dinámico, como lo muestra Brown y Smith (2011). Los métodos exactos de optimización presentan dificultades al tratar de encontrar soluciones para problemas con estas características, por lo que el uso de algoritmos heurísticos y metaheurísticos, tales como algoritmos genéticos, se ha ido incrementando en los últimos años (Chang, Yang y Chang, 2009), especialmente en la toma de decisiones financieras (Forbes, Hudson, Skerratt y Soufian, 2015). Por ejemplo, para el problema de selección de portafolios teniendo en cuenta los costos de transacción, Chen y Zhang (2010) implementa un Particle Swarm Optimization (PSO), Xia, Liu, Wang y Lai (2000) presenta un algoritmo genético y Chang, Meade, Beasley y Sharaiha (2000) considera tres algoritmos metaheurísticos: un algoritmo genético, una búsqueda tabú y un recocido simulado.
En este artículo se toma como alternativa de inversión la Bolsa de Valores de Colombia (BVC), la cual puede ser representada por el índice COLCAP. El COLCAP está compuesto por las acciones más líquidas de la BVC (mínimo 20), en donde la participación de cada una de ellas se calcula en función del valor de la capitalización bursátil ajustada. Los datos analizados corresponden a las acciones del índice COLCAP del primer trimestre de 2016, siendo este el periodo más reciente con información disponible al momento de iniciar la experimentación computacional y su respectiva validación. No obstante, la metodología planteada es totalmente independiente de las acciones utilizadas, y podría usarse cualquier periodo que se considere de interés. Los nemotécnicos, los nombres de las compañías y los sectores a los cuales pertenecen de acuerdo con la clasificación de la BVC se describen en la tabla 1. Nótese que el uso de las acciones del índice COLCAP favorece la obtención de un portafolio de alta liquidez, lo cual es de interés para los inversionistas y más aún cuando se tienen horizontes de tiempo cortos.
Tabla 1 Descripción de nemotécnicos
| Nemotécnico | Descripción | Sector |
|---|---|---|
| ECOPETROL | Ecopetrol S.A. | Industrial |
| PFGRUPSURA | Grupo Inversiones Suramericana | Inversiones |
| PFBCOLOM | Bancolombia S.A. | Financiero |
| GRUPOARGOS | Grupo Argos S.A. | Inversiones |
| NUTRESA | Grupo Nutresa S.A | Inversiones |
| CEMARGOS | Cementos Argos S.A. | Industrial |
| EXITO | Almacenes Éxito S.A. | Comercial |
| PREC | Pacific Rubiales Energy Corp | Industrial |
| ISAGEN | Isagen S.A. E.S.P. | Industrial |
| PFAVAL | Acciones y Valores S.A. | Financiero |
| CORFICOLCF | Corporacion Financiera Colombiana S.A. | Financiero |
| BOGOTA | Banco de Bogotá S.A. | Financiero |
| CLH | Cemex Latam Holding | Industrial |
| EEB | Empresa de Energía de Bogotá S.A. E.S.P. | Público |
| CELSIA | Celsia S.A E.S.P | Industrial |
| PFAVH | Avianca Holdings S.A | Industrial |
| ISA | Interconexion Eléctrica S.A. E.S.P. | Industrial |
| CNEC | Canacol Energy LTD | Industrial |
| BVC | Bolsa de Valores de Colombia S.A. | Financiero |
| PFDAV | Banco Davivienda S.A | Financiero |
| GRUPOSURA | Grupo Inversiones Suramericana | Inversiones |
| PFCEMARGOS | Cementos Argos S.A. | Industrial |
| BCOLOMBIA | Bancolombia S.A. | Financiero |
| PFGRUPOARGOS | Grupo Argos S.A. | Inversiones |
Fuente: elaboración propia.
Este trabajo presenta una herramienta que pueden utilizar los gerentes de proyectos para no asumir los costos de oportunidad en situaciones de exceso de liquidez. Dentro de todas las posibilidades que ofrece el mercado financiero (Frunza, 2016), se selecciona la Bolsa de Valores de Colombia como alternativa de inversión. A diferencia de Contreras, Bronfman y Arenas (2015), que también se concentra en el problema de selección de portafolios en la Bolsa de Valores de Colombia, en este trabajo se consideran los costos de transacción y en vez de un solo objetivo (Sharpe Ratio), se tienen en cuenta dos: maximizar la rentabilidad y minimizar el riesgo o varianza del portafolio (Problema Multiobjetivo), teniendo como restricción el presupuesto disponible del gerente de proyectos en ese momento. Además se presenta en un contexto de exceso de liquidez en proyectos, situación que aún no ha sido abordada por la literatura.
En este artículo se propone implementar un algoritmo metaheurístico multiobjetivo de optimización para construir un portafolio eficiente en mercados financieros, con el fin de encontrar alternativas de inversión que tengan una rentabilidad y un riesgo atractivos para el gerente de proyectos en situaciones de exceso de liquidez. Para lograr esto se presenta un modelo de optimización basado en el modelo de media-varianza propuesto por Markowitz, teniendo en cuenta los costos de transacción y restricciones de presupuesto, con el fin de resolver el problema de selección de portafolios en mercados financieros. Luego se implementa un algoritmo genético multiobjetivo basado en el Non-dominated Sorting Genetic Algorithm II (NSGA-II) (Deb, Pratap, Agarwal y Meyarivan, 2002), con el fin de encontrar portafolios eficientes en la Bolsa de Valores de Colombia. Finalmente, se analiza el impacto de las características específicas del modelo propuesto, como el presupuesto y los costos de transacción, en las variables de desempeño del portafolio como apoyo a la toma de decisiones financieras en proyectos.
Luego de esta introducción, este documento se organiza de la siguiente forma: en la sección 2 se hace una revisión del estado del arte. Se continúa con una descripción del problema y una formulación matemática del mismo en la sección 3. La sección 4 describe el método de solución propuesto y luego, en la sección 5, se discuten los resultados computacionales obtenidos. El documento finaliza con las conclusiones en la sección 6.
2. Estado del arte
En este artículo se extiende el modelo de optimización de portafolios de tipo media-varianza mediante la inclusión de restricciones adicionales relativas a los costos de transacción, también conocidos como costos de comisión. En Yoshimoto (1996) se demuestra que ignorar los costos de transacción puede resultar en portafolios ineficientes. Problemas similares han sido abordados en la literatura mediante algoritmos evolutivos (Chen y Zhang, 2010; Ruiz-Torrubiano y Suárez, 2015; Chen, 2015) y heurísticos iterativos (Lobo, Fazel y Boyd, 2006). Por otra parte, Filomena y Lejeune (2012) comparan diferentes formulaciones matemáticas convexas, mientras que Mansini, Ogryczak y Speranza (2015) propone modelos lineales enteros mixtos para resolver el problema, considerando funciones lineales por tramos para representar algunas no linealidades. Por otro lado, Woodside-Oriakhi, Lucas y Beasley (2013) proponen un modelo de programación cuadrática entera mixta para el problema de rebalanceo de portafolios con costos de transacción. Aunque la optimización de portafolios de inversión con costos de transacción ha sido estudiada previamente en la literatura, a diferencia de los trabajos anteriores, este artículo plantea una metodología multiobjetivo en la cual se genera una frontera eficiente en una ejecución del algoritmo.
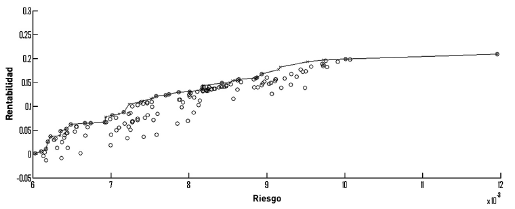
En el problema que se plantea se presentan dos objetivos que están en conflicto por naturaleza (rentabilidad y riesgo), por lo tanto, se deben utilizar algoritmos de optimización multiobjetivo para encontrar la frontera eficiente, también denominada frontera de Pareto (Nakayama, Yun y Yoon, 2009). En términos de portafolios de inversión, la frontera eficiente se refiere al conjunto de portafolios eficientes los cuales son todos aquellos que, para un nivel de rendimiento dado, son los que menor riesgo representan; o de manera análoga, aquellos que, para un nivel de riesgo dado, son los que mayor rentabilidad representan.
Como lo plantea Ehrgott y Gandibleux (2000), dado un conjunto de soluciones o portafolios X y un conjunto de Q funciones objetivo a minimizar z={ z 1 ,z 2 ,...,z Q}, un conjunto de portafolios S ∈ X es eficiente si no existe otro portafolio factible S' ∈ X tal que z j(S')≤z j (S) para todo j = {1,...,Q}, con estricta desigualdad para al menos uno de los objetivos. El conjunto correspondiente a z(S) = {z 1 (S),..,z Q(S)} es llamado no dominado.
En la figura 1, donde el eje vertical representa la rentabilidad y el horizontal el riesgo, cada solución obtenida se muestra como un punto en el plano. Para el caso particular, la frontera eficiente está dada por las cruces que están unidas por la línea recta, las cuales dominan el resto de soluciones o puntos.
Los algoritmos evolutivos (EA) multiobjetivo se han vuelto cada vez más populares debido a la aparición de nuevas clases de algoritmos y aplicaciones (Coello, 2005). Aunque hay muchas clases de EA, se pueden definir de manera general como procedimientos que consideran un conjunto de soluciones simultáneamente, llamado población. Se utilizan operadores de cruce o recombinación y de mutación para crear nuevas soluciones o individuos. Los mejores individuos o con mayor aptitud tienen mayor probabilidad de generar descendencia y de componer la población de la siguiente generación o iteración. Diferentes formas de evaluar la calidad de los individuos, de recombinarlos, de mutarlos, de actualizar la población, entre otros, produce las diferentes clases de algoritmos. El hecho de considerar un conjunto de soluciones permite a estos algoritmos encontrar múltiples soluciones de la frontera eficiente en una ejecución del algoritmo, en lugar de realizar series de ejecuciones separadas. Adicionalmente, los EA son menos sensibles a la forma, continuidad y otras propiedades matemáticas de la frontera eficiente (Coello, 2005).
En optimización de portafolios los EA han sido utilizados por Mishra, Panda y Majhi (2014), Ponsich, Jaimes y Coello (2013), Rodríguez, Cortez, Méndez y Garza (2015), Chen (2015), Chen et al. (2010), Chang et al. (2000), Soleimani, Golmakani y Salimi (2009) , Metaxiotis y Liagkouras (2012), Suksonghong, Boonlong y Goh (2014), Doerner, Gutjahr, Hartl, Strauss y Stummer (2004), entre otros.
Entre los algoritmos evolutivos multiobjetivo se destacan el Multi-Objective Genetic Algorithm (MOGA) (Fonseca y Fleming, 1995), Pareto Archived Evolution Strategy (PAES) (Knowles y Corne, 2000), Strength Pareto Evolutionary Algorithm-II (SPEA-II) (Zitzler, Laumanns y Thiele, 2001), y Non-Sorted Genetic Algorithm II (NSGA-II) (Deb et al., 2002), los cuales se describen brevemente a continuación.
En el MOGA, la aptitud de cierto individuo corresponde al número de individuos en la población actual por el cual es dominado. Todos los individuos no dominados se les asigna un ranking o aptitud igual a 1, mientras que los dominados son penalizados de acuerdo a la densidad de población de la región correspondiente. La función de aptitud se calcula de la siguiente forma: primero se organiza la población de acuerdo al ranking. Se continua calculando la aptitud de los individuos interpolando desde el mejor (ranking 1) hasta el peor, de la forma que propone Goldberg (1989), de acuerdo a alguna función, normalmente lineal, pero no necesariamente. Finalmente, se promedia el ajuste de los individuos con el mismo ranking, de tal forma que todos ellos estén incluidos en la misma categoría. Este procedimiento conserva constante el ajuste de la población global manteniendo una presión selectiva apropiada, como lo define la función usada.
El PAES utiliza una estrategia (1+1) de evolución (un solo padre genera una sola descendencia) en combinación con un archivo que guarda el histórico de las soluciones no dominadas previamente encontradas. Este archivo es usado como conjunto de referencia contra el cual cada individuo mutado es comparado. Un aspecto interesante de este algoritmo es el procedimiento utilizado para mantener la diversidad, el cual consiste en un procedimiento de hacinamiento que divide el espacio objetivo de una manera recursiva. Cada solución es ubicada en cierta posición basada en los valores de sus objetivos (los cuales son usados como coordenadas o posición geográfica). El mapa resultante se conserva, indicando el número de soluciones que residen en cada posición. Como el procedimiento es adaptativo, no se requieren parámetros extras (excepto por el número de divisiones del espacio objetivo).
El SPEA-II se construye a partir de su predecesor, el SPEA (Zitzler y Thiele, 1999). El SPEA utiliza un archivo que contiene soluciones no dominadas previamente encontradas. En cada generación, los individuos no dominados son copiados en un conjunto externo no dominado. Para cada individuo en este conjunto externo, se calcula un valor de fuerza o strength. Esta fuerza es similar al valor del ranking del MOGA, ya que es proporcional al número de soluciones a las cuales cierto individuo domina. En el SPEA, la aptitud o fitness de cada individuo en la población actual se calcula según las fuerzas o strengths de todas las soluciones externas que lo dominan. Adicionalmente, una técnica de clustering llamada average linked method (Morse, 1980) es utilizada para preservar la diversidad. El SPEA-II presenta tres diferencias con respecto a su predecesor: (i) incorpora una estrategia de asignación de ajuste fino que tiene en cuenta para cada individuo el número de individuos que domina y que lo dominan; (ii) utiliza una técnica de estimación de densidad del vecino más cercano que hace la búsqueda más eficiente, y (iii) tiene un método mejorado de truncamiento que garantiza la preservación de soluciones en la frontera.
En esta investigación se desarrolla un algoritmo genético basado en el método NSGA-II, el cual se detalla en las siguientes secciones. En Zhou, Qu, Li y Zhao (2011) y Coello (2005) el lector puede encontrar una revisión del estado del arte de algoritmos evolutivos multiobjetivo.
En los últimos años, a pesar del desarrollo creciente en la capacidad de cómputo, la complejidad de los modelos de optimización ha hecho que investigadores concentren sus esfuerzos en el desarrollo de algoritmos metaheurísticos, los cuales están basados principalmente en los fenómenos biológicos, sociales o físicos observados en la naturaleza. En Ponsich et al. (2013) , por ejemplo, se hace una revisión del estado del arte de diferentes propuestas aplicadas al problema de selección de portafolios. Dentro de ellas se encuentran los algoritmos genéticos, que fueron propuestos por primera vez por Holland (1992). Este tipo de algoritmos, así como otros algoritmos evolutivos, poseen características que los hacen particularmente útiles para la solución de problemas multiobjetivo, como el uso de múltiples soluciones. Los algoritmos genéticos se basan principalmente en el principio de Darwin: ''sobrevive quien mejor se adapte''. Al igual que la evolución biológica, en donde los individuos con los genes más aptos son los que mayores probabilidades tienen de sobrevivir, en los algoritmos genéticos las mejores soluciones son las que tienen una mayor probabilidad de sobrevivir y generar descendencia.
En los algoritmos genéticos, una población inicial (de individuos o soluciones) contiene un número determinado de cromosomas generados de manera que se garantice diversidad. En el contexto de optimización de portafolios, cada cromosoma representa la proporción w i que cada activo tiene en el portafolio. Se define una función de aptitud (evaluación) con el fin de evaluar cada cromosoma y así determinar cuáles de ellos representan una buena solución. Utilizando métodos de cruce entre cromosomas y mutaciones para generar nuevas soluciones, la población converge a un conjunto con las soluciones mejor adaptadas. El cruce entre cromosomas se refiere a una solución (hijo) obtenida al combinar otras dos o más soluciones (padres), mientras que la mutación ocurre bajo cierta probabilidad y trae como consecuencia un cambio aleatorio en una solución obtenida (hijo), como por ejemplo la inclusión o remoción de una acción aleatoria en el portafolio. Los componentes básicos de un algoritmo genético se presentan a continuación:
Paso 1: generar una población inicial diversa.
Paso 2: evaluar cada individuo de la población inicial.
Paso 3: seleccionar los individuos de la población para generar nuevos individuos hijos.
Paso 4: realizar la operación de cruce entre los individuos seleccionados.
Paso 5: actualizar la población actual con la nueva generación.
Paso 6: si las condiciones para que el algoritmo se detenga se cumplen, parar, de otro modo ir al paso 2.
Entre los algoritmos genéticos multiobjetivo destacados en la literatura se encuentra NSGA-II (Metaxiotis y Liagkouras, 2012), propuesto por Deb et al. (2002), el cual adapta la estructura de los algoritmos genéticos para tratar problemas con múltiples objetivos. Éste utiliza un método de dominancias para guiar a los individuos a la frontera eficiente, en donde un individuo es dominado por otro si tiene menor rentabilidad y mayor riesgo. En primer lugar, los individuos no dominados son identificados con el fin de constituir la primera frontera no dominada de ranking 1. El ranking de una solución indica el nivel de dominancia de la misma. Así, luego se clasifican progresivamente los individuos en fronteras eficientes con ranking k si solo son dominados por individuos pertenecientes a fronteras con ranking menor a k. El mecanismo de distancia de hacinamiento o Crowding Function se utiliza para preservar la diversidad en la población, discriminando entre individuos con el mismo ranking. Finalmente, el operador de actualización intenta conservar los individuos con ranking más bajo y distancia de hacinamiento más alta.
3. Descripción y formulación matemática del problema
En esta sección se presenta la descripción del problema de optimización y una formulación matemática del mismo. Para este caso se trata de un modelo multiobjetivo no lineal entero mixto para el problema de selección de portafolios con costos de transacción y presupuesto limitado. Adicionalmente, en lugar de definir la participación de cada tipo de acción en el portafolio por medio del porcentaje de inversión, este modelo define la cantidad de acciones a comprar de cada tipo de acción para discretizar el espacio de solución con el fin de reducirlo y ajustarlo a la realidad.
El problema de selección de portafolios con las características ya descritas puede ser expresado de la siguiente forma:
Dado un conjunto N = {1,2,...,n} de n acciones y un presupuesto limitado B, se desea conocer la cantidad de acciones a comprar de cada tipo de acción en el mercado.
Cada tipo de acción i ∈ N tiene una rentabilidad esperada r i, un precio p i y costo de transacción v i . Se asume, sin pérdida de generalidad, que todos los valores r i, p i y v i son estrictamente positivos. Por otro lado, para cada par de acciones (i,j),donde i, j ∈ N, σ ij = σ ji representa la covarianza entre ambos tipos de acciones. Nótese que σ 2 ii representa la varianza de la acción i.
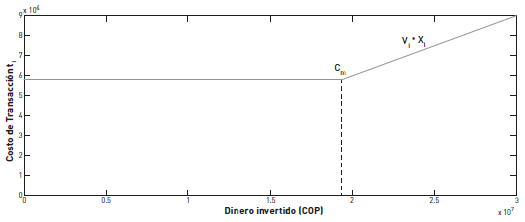
Cada vez que se invierte en una acción i, se deben tener en cuenta dos tipos de costos: el costo de compra de la acción, el cual es variable, y el costo total de transacción, que puede ser fijo o variable. En la BVC, así como en otros mercados financieros, se utiliza una estructura mixta para el costo de transacción. En la figura 2 se observa una representación del comportamiento de los costos de transacción con base en la estructura real actual de algunos comisionistas de la BVC. Para cualquier inversión, el costo de transacción debe ser mayor que un valor fijo t m. Sin embargo, para inversiones superiores a cierto monto C m , toma la forma v i • x i, donde v i representa una comisión en porcentaje para una inversión x i en la acción i. Así, el costo de transacción t i puede ser expresado como el máximo entre ambos: t i = max {t m ,v i •x i}.
La siguiente ecuación es una representación matemática de la función en la figura 2.
Adicionalmente, se puede notar que, como cada acción i tiene asociado un precio p i, el problema no está definido en términos de la cantidad de dinero x i invertido en cada acción, como en el problema original en Markowitz (1952), sino del número de acciones n i adquiridas.
El problema descrito tiene dos funciones objetivo. La primera consiste en maximizar la rentabilidad total del portafolio R p, mientras que la segunda busca minimizar el riesgo del mismo. En este modelo, se utiliza la varianza del portafolio V p para representar el riesgo del portafolio. Estas dos funciones objetivos son las dos más comunes en la literatura. Un tercer objetivo utilizado por los inversionistas se relaciona con maximizar la liquidez. En este modelo dicho objetivo no es formulado explícitamente ya que puede ser tenido en cuenta limitando las acciones disponibles a aquellas con mayor liquidez en el mercado.
Es importante resaltar que la primera función objetivo y todas las restricciones son funciones lineales, y que la única ecuación no lineal es la segunda función objetivo, asociada al riesgo. Esto es importante debido a que los modelos presentados en la literatura utilizan funciones no lineales para representar los costos de transacción. Por otro lado, la presencia de variables enteras y binarias afecta la convexidad y la complejidad del problema.
Este modelo matemático tiene en cuenta las siguientes variables de decisión: n i es el número de acciones de tipo i en el portafolio, t i corresponde al costo de transacción incurrido al adquirir la participación en las acciones i en el portafolio, y y i es una variable de decisión binaria que indica, para la acción i, si el número de acciones adquiridas es cero (y i = 0) o es un número positivo (y i = 1). Nótese que con estas variables de decisión, la cantidad de dinero invertido en acciones de tipo i puede ser expresada como x i = p i • n i, y el costo total asociado a la adquisición de las acciones de tipo i como p i • n i + t i .
En este tipo de sistemas el costo de transacción tiene dos efectos. En primer lugar, para inversiones con bajo presupuesto, no es atractivo diversificar el portafolio ya que los costos de transacción pueden volverse muy representativos frente a lo realmente invertido. Y en segundo lugar, se debe considerar la disminución de la rentabilidad global del portafolio debido a dichos costos.
La función objetivo relativa a la rentabilidad puede ser deducida de la siguiente definición:
Reemplazando los respectivos valores se obtiene la siguiente función no lineal:
Finalmente, se puede asumir que el inversionista desea invertir la totalidad del presupuesto disponible, esto es 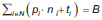 , por lo que la rentabilidad total puede ser reescrita como:
, por lo que la rentabilidad total puede ser reescrita como:
Ahora, como el presupuesto B es un valor constante, maximizar dicha función objetivo es equivalente a maximizar los beneficios, la cual puede ser escrita como:
Lo anterior implica que, aunque los valores de beneficios y rentabilidad no son iguales, los portafolios obtenidos por el modelo de optimización si lo son.
Se debe tener en cuenta que la inclusión de los costos de transacción implica una reducción en la rentabilidad igual a 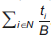 .
.
Cuando no se tienen costos de transacción (ti = 0), la función objetivo puede ser expresada como:
Esta última ecuación es equivalente a la función objetivo utilizada por Markowitz (1952) cuando se reemplaza por pi • ni por xi.
Por lo tanto, el modelo matemático completo puede ser descrito por las ecuaciones (12) a (20):
Donde la ecuación (12) representa la función objetivo relacionada con la maximización de la rentabilidad R p, mientras que la ecuación (13) corresponde a la minimización del riesgo, es decir, la varianza del portafolio V p. Las restricciones (14) indican que cuando un tipo de acción i ∈ N pertenece al portafolio (y i = 1), el máximo número de unidades puede ser B/p i y, cuando no pertenece (y i = 0), el número máximo de unidades es cero (n i = 0). La ecuación (15) limita el dinero invertido de acuerdo al presupuesto B. Las restricciones (16) y (17) limitan los costos de transacción para cada tipo de acción i. La ecuación (16) indica que el costo de transacción debido a un tipo de acción i ∈ N debe ser mayor que un valor fijo t m si dicha acción pertenece al portafolio (y i = 1) y, similarmente, la ecuación (17) indica que ésta debe ser mayor que un valor proporcional al número de acciones n i, el precio p i y la tasa v i. Finalmente, las restricciones (18), (19) y (20) definen el dominio de cada variable de decisión.
4. Método de solución propuesto
A continuación se describe el método de solución propuesto, el cual se basa principalmente en el algoritmo genético multiobjetivo conocido como NSGA-II (Deb et al., 2002). Los métodos para generar la población inicial, de actualización de población, los operadores de selección, cruce y mutación son adaptados específicamente para el problema planteado.
El algoritmo 1 resume el método de solución propuesto en esta investigación. En el ciclo entre las líneas 4 y 15, cada valor del contador gen representa una generación o iteración del algoritmo, donde nGen indica el número total de generaciones a realizar. Similarmente, en el ciclo entre las líneas 5 y 11 cada valor del contador hijo indica la creación de un hijo, donde nHijos representa el número de hijos creados en cada generación. En la línea 8, se genera un número aleatorio, el cual activa el operador de mutación si es inferior al parámetro pbbMut.
Algoritmo 1 - NSGA-II propuesto
1: Generar población inicial
2: Evaluar funciones objetivos de población inicial
3: Asignar ranking a individuos de acuerdo a función de dominancia
4: for gen ← 1 to nGen do
5: for hijo ← 1 to nHijos do
6: Operador de selección
7: Operador de cruce
8: if aleatorio < pbbMut then
9: Operador de mutación
10: end if
11: end for
12: Evaluar nueva población
13: Asignar ranking a individuos de acuerdo a función de dominancia
14: Actualizar población de acuerdo a función de hacinamiento
15: end for
En los algoritmos genéticos, así como en otros metaheurísticos, es común medir la aptitud de un individuo usando la función objetivo. Sin embargo, dado que el problema en estudio es de carácter multiobjetivo, el NSGA-II usa una función que asigna la aptitud de acuerdo al nivel de dominancia o ranking (líneas 3 y 13). En otras palabras, se clasifican progresivamente los individuos en fronteras eficientes con ranking k si solo son dominados por individuos pertenecientes a fronteras con ranking menor a k. En la figura 3 se presenta un ejemplo en el cual los puntos rellenos corresponderían a los individuos con ranking 1, mientras que los otros tres individuos tendrían ranking 2. Otra característica especial del NSGA-II es el uso de la denominada crowding function o función de hacinamiento para la actualización de la población (línea 14). Dicha función consiste en ordenar de mayor a menor las soluciones con el mismo ranking de acuerdo a la distancia que existe entre dichas soluciones y las dos soluciones adyacentes con igual ranking con el fin de favorecer la diversidad de soluciones. Para estimar el hacinamiento o densidad de soluciones alrededor de una solución particular en la población, se calcula la distancia promedio entre los dos puntos más cercanos hacia cada uno de los objetivos. Este valor sirve como estimación del perímetro de un rectángulo formado usando los puntos vecinos más cercanos como vértices. En la figura 3, la distancia de hacinamiento para la i-ésima solución en su frontera (marcada con círculos rellenos) es la longitud promedio de los lados del rectángulo mostrado con líneas punteadas.
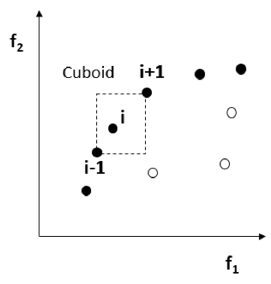
Fuente: elaborado con base en Deb et al. (2002).
Figura 3 Ejemplo de soluciones con diferentes rankings y cálculo de la distancia de hacinamiento.
Para representar una solución se utiliza un vector en donde el número de elementos representa la cantidad de tipos de acciones disponibles. Cada valor en dicho vector se encuentra entre cero y uno, y su significado corresponde a la proporción del presupuesto que se va a invertir en la respectiva acción una vez descontados los costos de transacción. Así, la suma de todos los elementos del vector debe ser igual a uno. La proporción invertida en cada acción tiene en cuenta los costos de transacción, así como también los precios de las mismas, por lo tanto el monto total invertido no necesariamente coincide con el presupuesto disponible. Por ejemplo, si se tiene un presupuesto de 10.000.000 de pesos colombianos (COP) y se desea invertir la totalidad del dinero en una acción con un valor de 27.500 COP, se obtendrían 359 acciones, se pagarían 116.000 COP de comisiones de compra, y quedaría un monto de 11.500 COP sin invertir.
Para determinar si una solución A es mejor que otra solución B, se deben evaluar sus respectivas funciones objetivo, rentabilidad y varianza. Si la solución A obtiene una mayor rentabilidad y una menor varianza que B se dice que A domina a B, por lo tanto, A es mejor solución que B. En otras palabras, el ranking de la solución A es menor que el ranking de la solución B. Por otro lado, si A tiene mayor rentabilidad que B, pero B tiene una menor varianza, no es posible determinar cuál de las dos alternativas es mejor. Cuando una solución no es dominada por ninguna otra solución se dice que dicha solución es no dominada. Así, el objetivo en los problemas multiobjetivo consiste en obtener un conjunto de soluciones no dominadas. El conjunto de soluciones no dominadas conforma la frontera eficiente o frontera de Pareto.
Los elementos a considerar para la configuración del algoritmo son: número de generaciones, población inicial (forma de generarla), tamaño de la población, operador de selección, operador de cruce, probabilidad de mutación y método de actualización de la población. Dichos elementos son descritos a continuación.
El número de generaciones representa el número de iteraciones que realiza el algoritmo. Para este caso los mejores resultados se obtienen utilizando 100 generaciones.
Para generar la población inicial en el algoritmo, se utiliza un método que se caracteriza por su tendencia a diversificar a medida que el presupuesto aumenta, y viceversa. Así, se asume una distribución exponencial con media para determinar el número de tipos de acciones en las que se debe invertir, de acuerdo con la ecuación (21). Nótese que cuando aumenta, la probabilidad de invertir en un número grande de acciones incrementa.
Una vez definido en número de acciones, las acciones específicas a invertir y el monto se eligen aleatoriamente.
El tamaño de la población indica el número de individuos o soluciones que son almacenados simultáneamente en cada iteración. Como valor se escogen 100 individuos en cada iteración. Además, en la implementación realizada en esta investigación el número de hijos generados en cada iteración es igual al tamaño de la población.
Los operadores de selección permiten seleccionar un conjunto de individuos de la población, en este caso dos, para combinar sus cromosomas y generar soluciones hijas. Se utiliza el método de selección por torneo que consiste en escoger 4 individuos diferentes aleatoriamente, los cuales posteriormente son divididos en dos parejas para iniciar un torneo. De cada uno de estos dos enfrentamientos resulta un ganador, correspondiente a aquel con mayor aptitud (ranking). Éstos dos individuos, llamados padres, son los elegidos para hacer el cruce.
Los operadores de cruce permiten al algoritmo generar nuevos individuos (hijos) con información genética de los padres. En este trabajo se implementa el cruce uniforme. En éste, en primer lugar se generan tantos números aleatorios como acciones disponibles hayan. En este caso el hijo se va construyendo con la información genética de un padre si el número aleatorio generado es menor o igual a 0,5, o con la del otro si es mayor. Para garantizar una solución en donde al menos se invierta en una acción, se selecciona una acción pivote cuya participación en el primer padre sea diferente de cero. En dicha acción pivote no se aplica el operador de cruce para evitar obtener una solución nula.
Los operadores de mutación permiten generar hijos con características que no están presentes en la población actual. Una vez hecho el cruce puede ocurrir una mutación de acuerdo a una probabilidad establecida (30% para el caso), lo que genera cambios aleatorios sobre un gen. El operador de mutación varía de acuerdo al individuo que debe ser mutado. El primer tipo de mutación corresponde al caso más general, en el cual el portafolio se compone de más de una acción y menos de n, y la mutación consiste en seleccionar una acción aleatoriamente y cambiarle su participación de forma aleatoria. En este caso, la acción seleccionada inicialmente puede o no hacer parte del portafolio original. El segundo tipo corresponde al caso en el cual el portafolio está compuesto por una sola acción. El procedimiento es similar, pero garantizando que la acción seleccionada al inicio no pertenezca al portafolio para obtener una solución diferente. El último caso corresponde a un portafolio en el que todas las acciones tienen participación diferente de cero en el portafolio. En éste se selecciona una acción aleatoriamente y se cambia su participación a 0%.
En la actualización de la población se conforma una nueva con el 30% de los mejores padres y el 70% restante con los mejores hijos. Los mejores individuos se seleccionan de acuerdo al ranking que cada uno tiene. Sin embargo, en caso de empate, se utiliza la Crowding Function para ordenar los individuos con el mismo ranking y así seleccionar los individuos más aislados de la población. Esto garantiza mayor diversidad en las nuevas generaciones.
5. Resultados computacionales
En esta sección se describen los experimentos realizados con el fin de analizar y comparar los resultados ante diferentes condiciones del problema. El algoritmo fue programado en MATLAB 2016, y las pruebas fueron ejecutadas en un computador con sistema operativo Windows 10, procesador Intel i7, 16GB de RAM y 4GHz.
Inicialmente, en la Sección 5.1 los experimentos se centran en el impacto que tiene el presupuesto disponible en la composición del portafolio. En la Sección 5.2 se comparan, para diferentes presupuestos, los resultados del algoritmo ante la presencia o no de costos de transacción. Finalmente, en la Sección 5.3, se valida el modelo propuesto en un caso aplicado en la gerencia de proyectos.
Para realizar las pruebas que se presentan a continuación se utilizan los precios de cierre diarios de las acciones del COLCAP durante el segundo semestre de 2015. Sin embargo, como ya se mencionó previamente, podría usarse cualquier periodo que se considere de interés.
5.1. Composición del portafolio para diferentes presupuestos
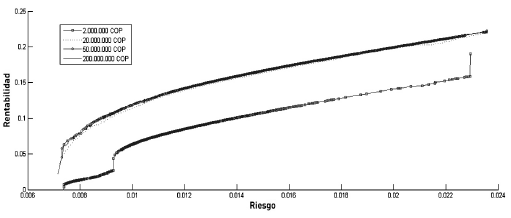
En los siguientes experimentos, se presentan los efectos de tener un presupuesto limitado B en la configuración del portafolio, el cual toma valores de 2.000.000, 20.000.000, 50.000.000 y 200.000.000 COP. Debido a la naturaleza multiobjetivo del problema abordado, se obtienen cuatro fronteras eficientes con varias soluciones para cada uno de los presupuestos.
En la figura 4 se presentan las fronteras eficientes para los presupuestos previamente mencionados. Las soluciones que aparecen como cuadrados unidos por una línea representan la frontera eficiente cuando el presupuesto a invertir es 2.000.000 COP. Se observa que esta frontera eficiente está muy por debajo de las otras 3 (línea punteada, línea unida por círculos y línea continua), las cuales no presentan una diferencia significativa entre ellas y se ven a simple vista como una sola línea ya que están superpuestas. Esto se explica principalmente por el impacto que tienen los costos de transacción en inversiones de montos bajos.
Al incrementar el monto invertido, la diversificación no se penaliza significativamente por dichos costos, lo que le permite al algoritmo encontrar portafolios más rentables con el mismo riesgo.
A continuación se analiza el impacto del presupuesto en cuatro puntos sobre la frontera eficiente. Los dos primeros son los extremos de la frontera, que están dados por la máxima rentabilidad y el mínimo riesgo. El tercer caso es un punto intermedio, que está expresado por el mínimo coeficiente de variación, el cual resulta de la división del riesgo sobre la rentabilidad. El último representa portafolios con diferente presupuesto, y una rentabilidad alrededor de 8,6%. Para estos experimentos se toman 10 presupuestos, siguiendo la expresión B n = B • n 2, donde B n es un presupuesto inicial de 2.000.000 COP.
5.1.1. Máxima rentabilidad
Al maximizar la rentabilidad, el algoritmo converge siempre a una única solución, que es aquella que obtiene mayor rentabilidad en el periodo evaluado. Este comportamiento es el esperado dado que en este criterio el riesgo no es importante. Por otro lado, la rentabilidad de cada portafolio, aunque tengan la misma composición, puede cambiar debido a los costos de transacción. La acción a invertir, de acuerdo al periodo de tiempo seleccionado es ISAGEN.
5.1.2. Mínimo riesgo
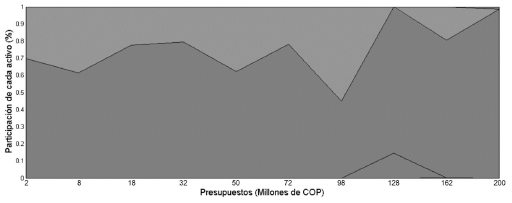
En la figura 5 el eje vertical representa la participación de cada activo dentro del portafolio y el eje horizontal los diferentes valores que puede tomar el presupuesto. Cada acción se representa en una escala de grises. Por ejemplo, para un presupuesto de 8 millones de COP, se presentan 4 escalas de grises, lo que significa que el algoritmo propone adquirir 4 acciones diferentes para dicho monto. Se observa que para disminuir el riesgo, el algoritmo sugiere la adquisición de varias acciones, entre 4 y 9 en promedio.
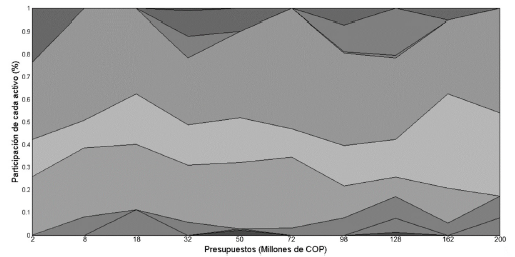
Fuente: elaboración propia
Figura 5 Composición de portafolio de mínimo riesgo para presupuestos variables.
No se identifica una tendencia definida a medida que se aumenta el presupuesto. Esto se explica debido a la no inclusión de los costos de transacción en la función objetivo asociada al riesgo, como se observa en la ecuación (7). Las diferencias en la composición de los portafolios se pueden atribuir al carácter estocástico del método de solución. Sin embargo, es importante resaltar que sin importar el presupuesto, siempre se invierte en las acciones de BOGOTA y EEB.
5.1.3. Mínimo coeficiente de variación
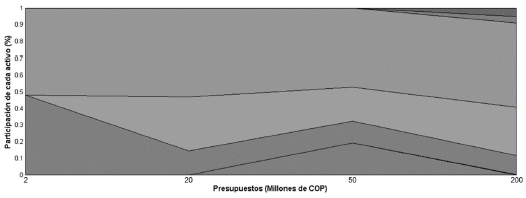
En la figura 6 se presenta la composición del portafolio que minimiza el coeficiente de variación. A medida que aumenta el presupuesto, la proporción invertida entre dos de las acciones (ISAGEN y CORFICOLCF) va variando hasta incluir una tercera y cuarta (CEMARG y CNEC) con los presupuestos más altos. Al igual que en el caso anterior, no hay diferencias significativas en el número de acciones, representadas por las diferentes tonalidades de gris.
5.1.4. Rentabilidad alrededor de 8,6%
Para este caso se toman los presupuestos definidos en la sección 5.1: 2.000.000, 20.000.000, 50.000.000 y 200.000.000 COP. En la figura 7 se muestra cómo al aumentar el presupuesto y manteniendo una rentabilidad definida, el algoritmo tiende a diversificar y por ende, a disminuir el riesgo. Cabe resaltar que en todos los casos de este ejemplo se invierte una porción del presupuesto en ISAGEN y en EEB. Sin embargo, para presupuestos superiores 2 millones de COP dichas porciones disminuyen y se incluyen otras acciones representadas por diferentes tonos de gris.
5.2. Costos de transacción
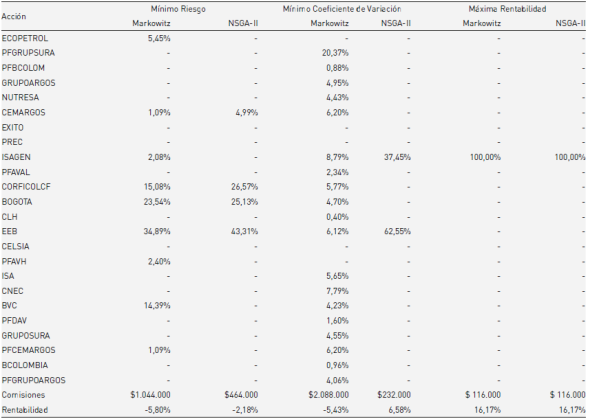
En esta sección se busca analizar el impacto de los costos de transacción en las soluciones, número de activos y valores de la función objetivo. Para esto se comparan los resultados del algoritmo propuesto contra los portafolios obtenidos a partir del modelo clásico de Markowitz. Dicha comparación se presenta en la tabla 2, en donde se contrastan los portafolios de mínimo riesgo, de mínimo coeficiente de variación y de máxima rentabilidad de cada uno de los métodos, para una inversión en la BVC de 10.000.000 COP. Los portafolios se construyen con datos del segundo semestre de 2015 y son evaluados en el primer semestre de 2016.
En las últimas dos filas de la tabla 2 se encuentran los valores correspondientes a las comisiones y rentabilidad de los portafolios. Note que el modelo de Markowitz no considera comisiones, sin embargo, son recalculadas con el fin de realizar la comparación entre rentabilidades.
Al ignorar los costos de transacción, el modelo de Markowitz tiende a diversificar el portafolio invirtiendo en muchas acciones. Esto trae como consecuencia una disminución en la rentabilidad por los altos costos en las comisiones de compra y venta de activos que se tienen en la vida real. Por ejemplo, el portafolio que minimiza el coeficiente de variación en el modelo de Markowitz sugiere la compra de casi todas las acciones del COLCAP, lo que en un escenario realista como el que se estudia resultaría inviable por dichos costos. Para el caso de la mínima varianza, el algoritmo propuesto también presenta una mejor rentabilidad (aunque negativa). Sin embargo, para el escenario donde se maximiza la rentabilidad, ambos métodos proponen la misma solución como alternativa de inversión.
5.3. Caso de aplicación
En esta sección se presenta un caso de aplicación en el cual se utiliza el ejemplo mencionado en la Sección 1, en donde los periodos se interpretan como semestres y se tiene en cuenta el segundo de 2015. Siguiendo los flujos de caja allí planteados, se tiene que para el primer semestre de 2016 se cuenta con un exceso de liquidez de 200.000 USD, que a la TRM de enero de 2016 ($3.149 COP/USD) equivalen a 629.800.000 COP. Teniendo esto en cuenta, se utiliza el modelo planteado para ver si la BVC sirve como una alternativa de inversión para que dicho exceso de liquidez no se convierta en un costo de oportunidad, sino que por el contrario retorne beneficios adicionales.
Por lo tanto, se empieza ejecutando el algoritmo con los datos del COLCAP del segundo semestre de 2015 con el fin de encontrar los portafolios eficientes y presentar tres escenarios para el gerente de proyectos: uno de máxima rentabilidad, uno de mínimo riesgo y otro intermedio, que se calcula como el de mínimo coeficiente de variación. Una vez hecho esto se simulan los resultados que se hubieran obtenido con cada uno de los portafolios durante el primer semestre de 2016, para evaluar con un caso el modelo y el algoritmo planteado.
En el caso de mayor rentabilidad, el algoritmo sugiere invertir todo el capital únicamente en ISAGEN, que fue la acción que mayor rentabilidad obtuvo en el segundo semestre de 2015, con una valorización del 22,58%. Con esta posición de alto riesgo, el gerente de proyectos hubiera obtenido una rentabilidad para el primer semestre de 2016 de 16,4%. Con esto, la TIRM del proyecto hubiera sido de 21,5%.
Para un escenario de mínimo riesgo, el algoritmo encuentra una solución invirtiendo de la forma que se muestra en la tabla 3. Teniendo en cuenta los costos de transacción, la rentabilidad al finalizar el primer semestre de 2016 de este segundo portafolio hubiera sido de 2,20 %, con lo que la TIRM del proyecto sería de 12,3%.
Tabla 3 Portafolio de mínimo riesgo
| Acción | Inversión (%) |
|---|---|
| PFBCOLOM | 1,69% |
| ISAGEN | 5,50% |
| CORFICOLCF | 31,79% |
| BOGOTA | 17,49% |
| EEB | 25,42% |
| BVC | 17,38% |
| PFCEMARGOS | 0,73% |
Fuente: elaboración propia.
Como última alternativa, el gerente de proyectos podría elegir el portafolio de menor coeficiente de variación, el cual se presenta en la tabla 4. Para este último caso, el gerente de proyectos tendría una rentabilidad del 4,62% y una TIRM del 13,9%.
Tabla 4 Portafolio de mínimo coeficiente de variación
| Acción | Inversión (%) |
|---|---|
| CEMARGOS | 2,78% |
| ISAGEN | 31,55% |
| EEB | 58,55% |
| CNEC | 1,84% |
| PFCEMARGOS | 5,20% |
Fuente: elaboración propia.
En cualquiera de los tres casos analizados, el gerente de proyectos hubiera obtenido una TIRM mayor a 10,9 % que se obtendría si no se reinvirtiera el exceso de liquidez.
6. Conclusiones
En esta investigación se combinan conceptos provenientes de diferentes áreas de conocimiento. El contexto del problema proviene de la gerencia de proyectos y de la necesidad de aumentar la rentabilidad de los mismos. Como alternativa para aumentar dicha rentabilidad se toma de las finanzas la evaluación financiera, y los conceptos de portafolio y riesgo. Finalmente, se toman de las matemáticas aplicadas y la investigación de operaciones las técnicas y algoritmos de optimización para problemas multiobjetivo.
Este artículo propone un modelo cuadrático de optimización. Este modelo está compuesto por restricciones lineales, una función objetivo lineal y una función objetivo cuadrática. Dicho modelo, aunque no es utilizado explícitamente para hablar portafolios eficientes, tiene características matemáticas que no han sido utilizadas por otros autores. Por otro lado, usar este modelo para hallar la frontera eficiente implicaría ejecutar sucesivamente un algoritmo que resuelva este modelo.
Se implementa un algoritmo genético basado en el NSGA-II para encontrar portafolios eficientes en la BVC. A través de datos reales y con un ejemplo aplicado, se muestra que los mercados financieros pueden convertirse en una alternativa atractiva para que los gerentes de proyecto inviertan el exceso de liquidez y mejoren la rentabilidad del proyecto.
En la comparación que se realiza con el modelo clásico de Markowitz, se comprende el impacto que tienen los costos de transacción y el presupuesto en la composición de portafolios. Para montos bajos de inversión, los costos de transacción hacen que el algoritmo propuesto concentre la compra en pocos activos. Esto, a diferencia del modelo de Markowitz, disminuye las comisiones y le dan una mejor rentabilidad al gerente de proyectos. Para los casos donde la inversión es alta, los costos de transacción no resultan significativos en cuanto a la composición de los portafolios cuando se comparan ambos métodos.
Aunque el algoritmo propuesto ha mostrado un gran potencial en la solución de problemas de optimización de portafolios de inversión con múltiples objetivos, a la hora de la implementación es necesario utilizar criterios adicionales para apoyar la toma de decisiones del gerente de proyectos o usuario final. Por otro lado, el algoritmo propuesto utiliza una población o conjunto de soluciones iniciales, así como operadores genéticos diseñados particularmente para el problema particular, los cuales ayudan al algoritmo a obtener fronteras eficientes con mayor diversidad de portafolios.
Sin embargo, los datos con los que se construye el portafolio pueden determinar el éxito o fracaso del mismo. Por lo tanto, el entorno macroeconómico resulta de gran importancia a la hora de aplicar el modelo planteado. Por esta razón, se propone como trabajo futuro incluir en el modelo la posibilidad de recomposición del portafolio, esto con el fin de reaccionar a tiempo ante los cambios que vive día a día el mercado. La recomposición de portafolios puede considerar técnicas relacionadas con indicadores y análisis técnico, o con modelos que consideren el costo de vender una posición en el mercado al sugerir la compra de una nueva posición.
Otras direcciones de investigación futura pueden considerar la inclusión de restricciones o características adicionales de los mercados financieros o los inversionistas, como la existencia de dividendos, limitar las soluciones a portafolios con características específicas (poco riesgosos, rentabilidad mayor a un valor dado, etc.), entre otras.
Algunos autores han propuesto también la consideración de diferentes medidas de riesgo como el Valor en Riesgo (o Value at Risk - VaR) propuesta por Linsmeier y Pearson (1996), el valor en riesgo condicionado (o Conditional Value at Risk - CVaR) introducida por Rockafellar y Uryasev (2000), la desviación absoluta media, entre otros.