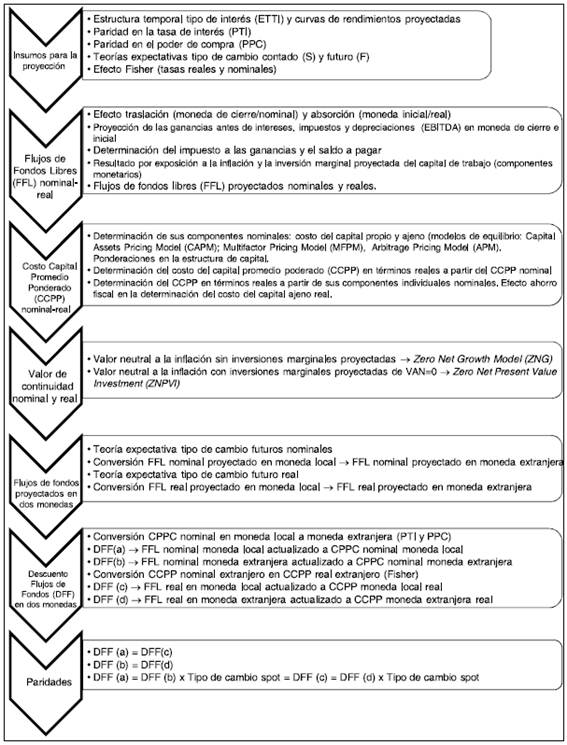
Fuente: elaboración propia.
Figura 1 Modelo de valuación en dos monedas en mercados emergentes.
Artículo
DOI: 10.1016/j.estger.2017.10.001
Valuación de empresas: enfoque integral para mercados emergentes e inflacionarios
Company valuation: integral approach for emerging and inflationary markets
Avaliação de empresas: abordagem integral para mercados emergentes e inflacionários
Gastón Silverio Milanesi*
* Profesor titular, Departamento de Ciencias de la Administración, Universidad Nacional del Sur, Buenos Aires, Argentina. Autor para correspondencia. San Andrés 800 Campus Universitario, 8000 Bahía Blanca, Departamento Ciencias de la Administración, Universidad Nacional del Sur, Buenos Aires, Argentina. Correo electrónico: milanesi@uns.edu.ar
Recibido 03 de Febrero de 2017
Aceptado 03 de Octubre de 2017
On-line 8 de diciembre de 2017
Resumen
En contextos inflacionarios los fundamentos de las teorías de paridad son requeridos por el modelo de descuento de flujos de fondos para asegurar la solidez de sus resultados, aspecto frecuentemente descuidado por los practicantes. En tal sentido se propone un método integral basado en las teorías de la paridad, con el objetivo de traer soluciones técnicas sobre las variables del modelo y estimar valores intrínsecos consistentes expresados en dos monedas. Inicialmente, se exponen el conjunto de teorías, herramientas y pasos secuenciales del modelo. Posteriormente, con un caso de aplicación y análisis de escenarios se examina su funcionamiento. Los resultados obtenidos aseguran relaciones entre valores intrínsecos en dos monedas, partiendo de magnitudes nominales y reales, apoyado sobre las teorías de paridad.
Palabras-clave: Inflación; Descuento de flujos de fondos; Teoría de la paridad; Valuación
Códigos JEL: G31. M21. F31.
Abstract
In order to guarantee the strength of its results at inflationary contexts, the foundations of the parity theories are required by the discount cash flow model, an aspect that is not frequently taken into consideration by the practitioners. In that sense, we propose an integral method based in the parity theories, with the aim of bringing technical solutions over the model variables and estimating consistent intrinsic values expressed in two currencies. First, the conjunct of theories, the tools and the sequential steps of the model are stated. Next, with an application case and scenarios techniques, its functioning is examined. The results secure the relationship between intrinsic values in two currencies, starting with nominal and real magnitudes, and supported by the parity theories.
Key words: Inflation; Discounted cash flow; Parity theorym; Valuation
JEL classification: G31. M21. F31.
Resumo
Em contextos inflacionários, os fundamentos das teorias de paridade são exigidos pelo modelo de descontó de fluxo de caixa com objeto de garantir a solidez de seus resultados, um aspecto frequentemente negligenciado pelos praticantes. Neste sentido, propõe-se um método integral baseado nas teorias da paridade, com o objetivo de obter soluções técnicas nas variáveis do modelo e estimar valores intrínsecos consistentes expressos em duas moedas. Inicialmente, o conjunto de teorias, ferramentas e etapas sequenciais do modelo são expostos. Mais tarde, a sua operação é examinada com um caso de aplicação e análise de cenários. Os resultados obtidos asseguram relações entre os valores intrínsecos em duas moedas, a partir de magnitudes nominais e reais, suportadas pelas teorias de paridade.
Palavras-Chave: Inflação; Desconto de fluxos de Caixa; Teoria da paridade; Avaliação
Classificações JEL: G31. M21. F31.
1. Introducción
La inflación en precios se caracteriza por su naturaleza no neutral, afectando tanto la demanda y oferta de bienes y servicios como la evolución de las relaciones entre los precios de los productos. Los efectos ocasionados por la inflación alcanzan a todos los actores de un sistema económico. En el caso de las empresas, la inflación impacta directamente en los conductores de valor, como los ingresos, las estructuras de costos y el costo de las fuentes de financiamiento. Por lo tanto, en contextos inflacionarios, los modelos de valuación de empresas deben contemplar los efectos que la inflación genera sobre las variables que hacen al valor de la firma. Así se logrará una medición coherente del valor intrínseco de la firma. No obstante, la teoría financiera entendida como el marco científico y cimiento teórico de los modelos de valuación de empresas, a menudo presenta propuestas metodológicas pensadas solamente para mundos caracterizados por la estabilidad de precios. Estas propuestas aplicadas directamente en contextos emergentes e inflacionarios, sin consideraciones sobre la inflación, derivan en conclusiones erróneas (Modigliani y Cohn, 1984).
Motivado por el argumento precedente el presente trabajo desarrollará una propuesta metodológica, destinada a la valuación de empresas en contextos emergentes e inflacionarios. Se explicita el uso del modelo de descuento de flujos de fondos (DFF)1, con variables expresadas en términos nominales y reales2, expresadas en moneda local y extranjera. En este sentido, el trabajo resume y expone todas las consideraciones técnicas, relativas al tratamiento de las variables que componen las magnitudes financieras proyectadas, el flujo de fondos libres, tasas de costo del capital y valor terminal. Todas expresadas en términos nominales y reales, tanto en moneda local como extranjera.
Respecto a las técnicas y herramientas utilizadas, estas son provistas por un importante cuerpo de publicaciones (Modigliani y Cohn, 1984; Copeland, Koller y Murrin, 2000; Titman y Grinblatt, 2002; Velez Pareja, 2006; Damodaran, 2006; Emery y Finnerty, 2007; Bradley y Gregg, 2008; Pratt y Grabowski, 2008; Tham y Velez Pareja, 2011; López Dumrauf, 2014b). De esta forma, el principal aporte consiste en vincular y sintetizar un conjunto de teorías, técnicas y procedimientos contenidos en los trabajos mencionados, para lograr una metodología de valuación, integral y coherente, en dos monedas, para contextos inflacionarios.
La estructura del trabajo es la siguiente: el punto de partida lo constituyen las teorías de paridad de poder de compra, tasas de interés, expectativas en los tipos de cambio y los modelos de pronóstico de curvas de tasas de interés. A continuación, se analizan las técnicas de proyección correspondientes a magnitudes financieras en moneda inicial y de cierre; determinación del costo promedio ponderado del capital; y cálculo del valor de continuidad neutral a la inflación. Los anteriores apartados son insumos a ser utilizados en la valuación con el descuento de flujos, en dos monedas. Para ilustrar el funcionamiento del modelo se utiliza el estudio de casos como metodología, seleccionándose una empresa en marcha como unidad de análisis, a los efectos de estimar su valor intrínseco con la propuesta metodológica del presente trabajo. Finalmente, se presentan las principales conclusiones obtenidas.
2. Modelo integral de valuación de empresa: el descuento de flujo de fondos, inflación y las teorías de paridad
En esta sección son desarrolladas brevemente las teorías, técnicas y herramientas a ser utilizadas para obtener las variables insumos del modelo de descuento de flujos de fondos en contextos inflacionarios, expresados en moneda local y extranjera.
El punto de partida está dado por las relaciones entre inflaciones esperadas y tasas de interés real y nominal, entre el mercado local y el extranjero. La lógica de las relaciones mencionadas es explicada por las teorías de paridad, propias de las finanzas internacionales y las técnicas para estimar las curvas de rendimientos. Las últimas son las proveedoras del primer insumo (las tasas nominales de interés esperadas), que permitirán proyectar tasas de inflación y tipos de cambios.
Seguidamente, se explicitarán el conjunto de variables que definen el valor de la firma y su tratamiento específico en contextos inflacionarios, a saber: proyección de los flujos en moneda de cierre e inicio; efectos generados por la inflación (resultados por exposición, rubros monetarios, corrección de precios y distorsión en la base imponible del impuesto a las ganancias); determinación del costo promedio ponderado del capital y estimación del valor de continuidad. Finalmente, las variables mencionadas serán utilizadas en el marco del descuento de flujos de fondos, estimando el valor intrínseco de la firma en moneda doméstica y extranjera, con magnitudes expresadas en términos nominales y reales. La coherencia del resultado obtenido está dada por las teorías de paridad y contenida en la propuesta del trabajo. La secuencia lógica correspondiente a la propuesta metodológica se expone en la figura 1.

Fuente: elaboración propia.
Figura 1 Modelo de valuación en dos monedas en mercados emergentes.
A continuación, será desarrollado el abordaje teórico del modelo comenzando por las teorías de la paridad y el efecto Fisher; la proyección de las curvas de rendimientos y el uso de bootstrapping; los conceptos de magnitudes financieras en moneda de cierre e inicial; las proyecciones de resultados y flujos de fondos libres con inflación; el costo del capital promedio ponderado; y el valor terminal incorporando las correcciones propias de los modelos neutrales a la inflación. En la última subsección será expuesto el modelo integral de descuento de flujos de fondos en moneda doméstica y extranjera, trabajando magnitudes en moneda de cierre e inicio.
2.1. Los insumos: las teorías de la paridad y el ''efecto Fisher''
A continuación son presentadas las cuatro teorías clásicas de paridad, que en condiciones de equilibrio de mercado explican las relaciones de valor entre tasas, inflación y tipo de cambio esperado correspondiente a dos países.
Paridad en la tasa de interés (PTI): manifiesta la relación entre tasas nominales de interés local (r t,d,n ) y extranjera (r t,e,n ) explicando la relación entre el tipo de cambio contado (spot) (S) y el tipo de cambio futuro nominal (F t,n ).
Paridad en el poder de compra (PPC): por la ley del precio único, el mismo bien negociado en dos mercados diferentes debe valer lo mismo en ambos mercados en términos de poder adquisitivo de la población. Si la ley se cumple, entonces en el mercado extranjero el bien A que cuesta $1 (unidad monetaria extranjera) debe valer lo mismo en el mercado doméstico $1 (unidad monetaria extranjera). La diferencia nominal en el valor del bien, entre dos países, la explica solamente el tipo de cambio entre la moneda extranjera y la moneda de curso legal del país bajo estudio. Por lo tanto, si la PPC se verifica, el tipo de cambio y el resto de los bienes deben ajustar su valor por el diferencial de tasas de inflación esperadas entre los dos países (Emery y Finnerty, 2007)3. Matemáticamente la relación es expresada como el cociente entre la tasa de inflación esperada doméstica y extranjera, que explica el diferencial entre el tipo de cambio contado y spot esperado, así:
De esta forma, utilizando la ecuación 2 se puede inferir la tasa de inflación para un periodo, como se muestra a continuación:
Teoría de expectativas del tipo de cambio esperado contado y futuro: implica que cuando el mercado se encuentra en equilibrio se cumple la convergencia entre el tipo de cambio futuro Ft,n y el tipo de cambio contado esperado para el horizonte del contrato futuro, tal que:
Efecto Fisher: implica que el mercado revela información sobre tasas de interés nominales incorporando en estas las expectativas inflacionarias. Esto se conoce como efecto Fisher4. A partir de tal concepto, se formaliza la distinción entre tasas de interés real y nominal, mediante la ecuación de Fisher (Argandoña, 2013). Por lo tanto, la tasa esperada nominal es:
Si el efecto Fisher es válido, la diferencia entre las tasas de interés para dos economías se explica por los diferenciales de inflación. En términos reales, la tasa queda expresada como:
El efecto Fisher supone que la tasa real entre ambos países r t,r debe ser similar y converger. Por lo tanto, la ecuación de arbitraje de Fisher entre tasas nominales y reales es la siguiente:
Despejando en función de la tasa nominal r t,d,n = (1 + π t,d )(1 + r t,r ) − 1, la tasa queda planteada de la siguiente manera:
Cabe destacar que un frecuente error de especificación reside en no considerar el segundo término de la ecuación. En efecto, a menudo, la relación es planteada de la siguiente manera: r t,d,n = r t,r + π t,r y para la tasa real r t,r = r t,d,n + π t,d 5.
2.2. Los insumos: la curva de rendimientos proyectada en mercados emergentes
Desde el punto de vista instrumental, estimar la PTI y PPC requiere de tasas de intereses proyectadas como insumos. Para ello, se debe calcular una curva teórica de rendimientos o estructura temporal de tipos de interés (ETTI), empleando títulos en moneda doméstica y extranjera emitidos por el mismo país. A partir de la PTI y PPC se supone que el diferencial entre tasas de interés esperadas, en moneda local y extranjera, captura la depreciación (apreciación) de la moneda doméstica frente a la divisa. Cabe destacar que un requisito metodológico de la ETTI es que esta debe construirse con tasas contado. Esto es posible en mercados financieros desarrollados con suficiente profundidad y liquidez6, siendo inconveniente en mercados emergentes. En su construcción son utilizadas diversas técnicas, las más comunes son el bootstrapping y el ajuste logarítmico.
Bootstrapping: a partir de bonos cupón cero a un año, se puede derivar el resto de los plazos con Treasury STRIPS7, en tanto y en cuanto estos tengan liquidez (mercado secundario). Si no se cumple el requisito de liquidez, el uso de STRIPS distorsiona la relación rendimientos y plazos de la curva spot. En esos casos, la técnica a la cual se recurre es el bootstrapping (Fabozzi y Fabozzi, 1996). Para ello son utilizados los bonos cupón cero con horizontes de corto plazo. El mediano y largo plazo se resuelve en orden ascendente utilizando tasas spot estimadas, que son calculadas por despeje respecto del último pago, a partir del uso de bonos tipo bullets8.
Ajuste logarítmico: es una técnica alternativa que consiste en derivar la curva de rendimientos de bonos, mediante regresión logarítmica entre la duración (duration) modificada9 y la tasa interna de retorno (TIR) de los bonos en moneda doméstica y extranjera. Con el ajuste logarítmico10 se obtiene una ecuación del estilo i t = α+ βln (t), en donde t representa el tiempo suponiendo rendimientos ascendentes. Su implementación requiere de bonos provenientes del mismo emisor, en moneda doméstica y extranjera con similares características de riesgo, liquidez, garantías, duración e interés fijo.
2.3. Proyecciones: valores nominales y reales. Efectos traslación y absorción
Las magnitudes financieras proyectadas pueden expresarse en moneda con poder adquisitivo de cada periodo, también conocida como de cierre o nominal, y en moneda con poder adquisitivo inicial, conocida como de inicio o términos reales. Estas son las dos alternativas para expresar las magnitudes financieras cuando se proyecta con inflación. En un proceso de valuación de empresas, no se debe perder de vista que una de las primeras tareas consiste en definir si la proyección se trabaja en moneda inicial (real) o en moneda de cada periodo (cierre). Esta elección es crucial, ya que condicionará la manera en la cual serán expresadas las variables del modelo de descuento de flujos de fondos.
Conforme fue indicado, las magnitudes nominales o expresadas en moneda de cierre son aquellas que contienen la inflación proyectada. En el otro extremo, los valores deflactados de inflación serán referenciados como cifras reales o expresadas en moneda inicial. En el primer caso, el acto de incorporar la inflación esperada a una cifra proyectada es conocido como traslación. La segunda manera de expresar las magnitudes monetarias implica quitar la inflación, expresando flujos futuros con poder adquisitivo del presente. Esto se conoce como absorción.
De esta forma, las magnitudes financiares nominales o en moneda de cierre (traslación) son estimadas utilizando un coeficiente que se construye a partir de un número índice, de base 1 en el momento t=0, conforme se expone a continuación:
Donde id es el índice y π t,1 es la evolución en el nivel de precios para (t) y el activo (i). Conforme fue indicado, la inflación proyectada es una variable obtenida de los datos provenientes de la curva de rendimientos, y de operar las ecuaciones de PTI y PPC. El coeficiente (nx t ) surge de:
Expresando la magnitud financiera en moneda de cierre (v t,n ),
Referente a las magnitudes financiares reales o en moneda inicial (absorción), la lógica es inversa al proceso anterior. Primero se debe calcular la variación relativa de precios para un ítem específico (Δπ t,i ). Para ello se construye un índice que relaciona la evolución del precio del flujo (π t,i ) y el índice general de precios (inflación general)11 (π t,g ), así:
Los valores nominales proyectados se deflactan empleando el coeficiente (rx t )
La magnitud en moneda inicial (V t,r ) se obtiene de:
Finalmente, las relaciones entre una proyección financiera expresada en términos nominales y reales tienen un común denominador: efectos absorción (ecuación 15) y traslación (ecuación 16);
Las magnitudes nx t,a y rx t,a son acumuladas hasta el momento t.
2.4. Descuento de flujos de fondos: magnitudes financieras proyectadas e inflación
Las variables requeridas por el modelo de descuento de flujo de fondos son: flujos de fondos proyectados correspondientes al horizonte explícito de proyección, la tasa de costo del capital12 y valor terminal (Copeland et al., 2000; Pratt y Grabowski, 2008). La presente sección abordará el tratamiento de la primer variable, la estimación de la medida flujos de fondos en moneda de cierre (efecto traslación, ecuación 16) y en moneda inicial (efecto absorción, ecuación 15).
a) Ingresos y costos en moneda de cierre: el primer ejercicio prospectivo en la determinación de ingresos y gastos proyectados consiste en estimar unidades esperadas para cada periodo del horizonte de proyección. Para ello se deben proyectar, en unidades, los niveles de producción (q p,t ) y ventas (q v,t ) como la política de inventarios13, ya que estos integran los rubros no monetarios del capital de trabajo estimado.
Los ítems indicados expresados en unidades son transformados en magnitudes financieras utilizando los precios proyectados que incorporan la inflación esperada. Por lo tanto, son proyectados precios unitarios de venta (PVU t,n ), costo variable (CVU t,n ) y el costo fijo unitario (CFU t,n ). Con estos datos se está en condiciones de estimar el costo total unitario CTU t,n = (CVU t,n + CFU t,n ). Cabe destacar que los costos e ingresos para cada periodo (t) surgen del producto entre precio en t-1 y el coeficiente (ecuación 10), así se tiene:
Los flujos de ventas y costos proyectados surgen del producto entre precios unitarios (ecuaciones 17,18 y 19) y cantidades proyectadas (q p,t , q v,t ). De esta manera, las magnitudes financieras obtenidas son: i) ingresos IT t,n = PVU t,n × q v,t ; ii) costos variables y fijos CVT t,n = CVU t,n × q p,t ; CFT t,n = CFU t,n × q p,t y iii) costos totales de producción CTP t,n = CTU t,n × q p,t .
Los inventarios juegan un rol importante, en particular para la estimación del capital de trabajo. Para estimar las unidades de inventarios finales (EF q,t ), su cálculo requiere de utilizar las unidades de ventas, producción y existencias iniciales (EI q,t ) proyectadas, conforme surge en la siguiente ecuación.
La valuación de las existencias surge del producto entre las cantidades por costo total unitario proyectado: EF q,t × CTP t,n = CTU t,n . El valor proyectado del costo de artículos vendidos (CAV t,n ) es obtenido de multiplicar las proyecciones de ventas y costo total unitario proyectado CAV t,n = CTU t,n × q v,t .
b) Impuesto a la ganancia: algunas legislaciones tributarias no reconocen el impacto de la inflación en la determinación del impuesto a las ganancias; por lo tanto, para estimar la base imponible el costo de artículos vendidos se computa a valores históricos. La estimación de las bases imponibles correspondientes al impuesto proyectado en cada periodo debe realizarse de manera separada de los resultados proyectados. Por lo general, las existencias iniciales (EI q,t ) están valuadas a su precio histórico, mientras que la producción q p,t y EF q,t por el costo total unitario corriente (CTU t,n ). Con tales consideraciones, el costo histórico computable a los efectos tributarios es: CAV t,H = (EI q,t × CTU t−1 ,n) + (q p,t × CTU t,n )− (EF q,t × CTU t,n )14. La base imponible proyectada del impuesto surge de la siguiente expresión:
Donde IT t,n representa a los ingresos del periodo, CAV t,H el costo de artículos vendidos histórico, CFT t,H el costo fijo histórico, A t,H amortización histórica y BI base imponible proyectada. El impuesto a las ganancias determinado proyectado (ID t ) surge del producto ID t = BI t × T, donde T representa la alícuota marginal. Si la legislación tributaria vigente dispone el ingreso de anticipos de pagos de impuestos (AP t ), la cifra de impuesto a pagar proyectado (IP t ) surge por diferencia entre el impuesto determinado y los anticipos ingresados en el periodo anterior (AP t−1 ) ; IP t = ID t – AP t−1 15.
c) La proyección del resultado operativo: primero debe proyectarse el EBITDA t en moneda de cierre. Este es calculado de la suma algebraica de las magnitudes monetarias proyectadas en términos nominales, IT t,n – CAV t,n – CFT t,n . En la siguiente ecuación, R Ot representa al resultado operativo después de impuestos. Este surge de restar al EBITDA t la amortización en moneda de cierre (A t,n ) y el impuesto a las ganancias proyectado determinado (ID t,n ).
d) Capital de trabajo, rubros monetarios y no monetarios: los elementos que integran el capital de trabajo proyectado deben ser separados, según su exposición a la inflación, en monetarios y no monetarios. En el caso de las partidas monetarias, la inflación produce un resultado negativo del activo (efectivo y cuentas a pagar sin indexación en moneda doméstica) y positivo producto del pasivo monetario (deudas sin indexación en moneda doméstica). Por lo tanto, la variación total correspondiente a la inversión incremental proyectada en capital de trabajo se descompone en:
Donde ΔCT representa el incremento total en el capital de trabajo, integrado por la variación de los componentes monetarios ΔCTM y no monetarios ΔCTNM. Respecto de los últimos, cabe destacar dos tratamientos para calcular el resultado por exposición a la inflación. Una primera alternativa consiste en calcular ΔCTM como la diferencia entre la magnitud inicial de cada partida expresada en moneda de poder adquisitivo del ejercicio anterior CTM (t−1),mi y la magnitud final expresada en moneda de poder adquisitivo de cierre (ejercicio presupuestado) CTM (t),mc 16. En este caso la variación total contiene el incremento real (aumento físico) y la variación nominal por exposición a la inflación (resultado proyectado por exposición a la inflación neto, (REI t )).
Otra alternativa consiste en expresar las magnitudes iniciales en moneda de poder adquisitivo de cierre; ΔCTM (real)t,n = CTM (t),mc – CTM (t−1),mc . La variación obtenida representa la efectiva inversión incremental o liberación de fondos. En este caso el resultado proyectado por exposición a la inflación se explicita como un componente más en el flujo de fondos proyectados en moneda de cierre (ecuación 24), siendo ΔCTM (total)t,n – ΔCTM (real)t,r = REI t . Para rubros no monetarios (inventarios), la variación real (inversión-desinversión) se obtiene comparando las magnitudes iniciales y finales expresadas en moneda de igual poder adquisitivo ΔCTNM (real)t,n = CTNM (t),mc – CTNM (t−1),mc
d) Flujos de fondos libres en moneda de cierre (FFL t,n ): surge de la suma de magnitudes monetarias vistas en el apartado anterior, agregando las inversiones incrementales en activos fijos operativos (ΔAF t,n ), así:
En la ecuación anterior la variación sobre el capital de trabajo monetario no depura el incremento real en las partidas monetarias. Si se aplica el segundo camino, debe incorporarse el efecto del resultado neto por exposición REI t .
e) Flujos de fondos libres en moneda inicial (FFL t,r ): se obtiene a partir del flujo de fondos libre en moneda de cierre (ecuación 25), deflactado (ecuación 15):
En el caso de estimar el flujo por el método indirecto, las magnitudes deben calcularse en moneda de poder adquisitivo inicial.
Para ello se deben emplear las ecuaciones 12,13 y 14 para elaborar el índice, coeficiente y transformación de magnitudes de nominales a reales. Seguidamente son estimados: el impuesto a las ganancias en términos reales, la inversión incremental real en capital de trabajo y el resultado del periodo por exposición a la inflación17.
f) Valor actual de los flujos: el valor actual será coherente en la medida que exista consistencia entre el poder adquisitivo en que se expresan flujos y tasa. Los flujos proyectados en moneda de cierre (nominal) deben actualizarse al costo del capital nominal, cuyo tratamiento será abordado en la próxima sección (ecuación 28).
Donde VA d,n representa el valor actual en moneda doméstica y ko n,t el costo del capital nominal. Con similar criterio los flujos proyectados en moneda inicial deben actualizarse al costo del capital real:
La tasa real del costo del capital es ko r,t , y las ecuaciones 28 y 29 deben conducir al mismo resultado18.
2.5. Descuento de flujo de fondos: costo del capital e inflación
Los efectos de la deuda sobre el valor del negocio están representados en el costo de capital promedio ponderado (CCPP o WACC). En términos nominales su expresión se representa mediante la siguiente ecuación;
Donde W e y W d representan ponderaciones de las fuentes de financiamiento con capital propio y deuda, ke n,t y ki n,t se refieren al costo del capital propio y de la deuda, siendo T la tasa marginal de impuesto a las ganancias. Aplicando la ecuación de Fisher, el costo del capital propio y ajeno en términos nominales se descompone en ke n,t = ke r,t + π t,d + (ke r,t × π t,d ) y ki n,t = ki r,t + π t,d + (ki r,t × π t,d ). La magnitud CCPP en términos reales se puede estimar de forma directa o indirectamente. El primer camino consiste en deflactar la ecuación 30 (Bradley y Gregg, 2008; Tham y Velez Pareja, 2011) de la siguiente manera:
El segundo camino consiste en estimarlo indirectamente, calculando en términos reales las tasas de cada componente del CCPP (ecuación 30). En este caso, uno de los errores de especificación más frecuente resulta del incorrecto tratamiento del ahorro fiscal sobre el costo del capital ajeno. A menudo, de manera incorrecta, se toma directamente la tasa nominal de la deuda antes de impuestos, para luego transformarla en real. Recién allí se incorpora el efecto del ahorro fiscal19. El punto de partida siempre debe ser el costo nominal de la deuda después de impuestos (ki
n,t
(1 −T)), y luego estimar la tasa real kidp
r,t
= 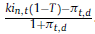 . La expresión del CCPP (deflactado) (Tham y Velez Pareja, 2011) es:
. La expresión del CCPP (deflactado) (Tham y Velez Pareja, 2011) es:
2.6. Descuento de flujo de fondos: valor de continuidad e inflación
El valor de continuidad, o también nombrado como valor terminal (VT), representa el valor actual correspondiente de los flujos de fondos esperados considerando un horizonte perpetuo. Para su estimación se utiliza el conocido modelo de descuento de dividendos con crecimiento constante (Gordon, 1962), adaptado a los conductores de valor (value driver) de la firma (Rappaport, 1998; Copeland et al., 2000; Brealey, Myers y Allen, 2006; Pratt y Grabowski, 2008). Siguiendo a Copeland et al. (2000), el valor terminal se puede expresar como:
La nueva variable es la tasa de crecimiento nominal esperada G y Rt la tasa de rendimiento nominal de la firma. La ecuación anterior surge de la clásica expresión,
Donde los flujos de fondos libres pueden plantearse en términos de FFLn,t = ROn,t × (1 − tr), siendo tr la tasa de reinversión o porcentaje del resultado reinvertido en el negocio cada año. Surge de la relación entre la tasa de crecimiento de los resultados G y la tasa de rendimiento de la firma Rt, donde G = Rt × tr, siendo la expresión de tasa de crecimiento de mayor difusión. Despejando, en función a la tasa reinversión, se obtiene que tr = G/Rt. Por lo tanto, el flujo de fondos libres es igual a FFLn,t = ROn,t × (1 − G/Rt) y se concluye como resultado en la ecuación 33.
Siguiendo a Bradley y Gregg (2008), a menudo se comenten errores de especificación con las variables del modelo, en particular con la forma de expresar la tasa de crecimiento y su tratamiento relativo de la inflación. Aplicando la paridad de Fisher, la tasa de rendimiento nominal (Rt) sobre los activos de la firma (CIt−1) queda expresada de la siguiente manera:
Siguiendo el mismo criterio, la correcta especificación de la tasa de crecimiento de los flujos de fondos libres de la firma debe ser la siguiente:
La ecuación precedente explica el crecimiento en términos nominales mediante dos componentes: i) la tasa de crecimiento en los flujos de fondos libres nominales generados por las nuevas inversiones (tr × Rt) y ii) el aumento en el valor nominal del activo fijo de la firma, producido solamente por efectos de la inflación ((1 − tr) × πt,d). Entonces hay dos elementos que conducen el crecimiento de los flujos: el primero es el incremento en los flujos de fondos nominales producto de las nuevas inversiones y el segundo se origina por el revalúo en procesos inflacionarios del capital, cuyo valor aumenta más que la inflación. No obstante, es el segundo término el ignorado por la literatura, especificando la tasa de crecimiento con la clásica expresión G = tr × Rt. Por lo tanto, el efecto de la inflación en la tasa de crecimiento de la firma dependerá de la tasa de reinversión (tr). Si esta es 0 entonces G = πt,d y todo el crecimiento es atribuible a la revaloración de la inversión en activos. Si es > 1 el aumento provocado por activos fijos se ve acompañado por un incremento en los flujos de fondos de nuevas inversiones. La conexión entre tasa nominal y real de crecimiento (g) es la siguiente: G = g + πt,d + g × πt,d, siendo la tasa real g = tr × r.
En el supuesto que no exista inversiones previstas la expresión que define el valor terminal se conoce como Zero Real Growth Model (ZRG). A partir de la expresión contenida en las ecuaciones 33 y 34 (caso general), sustituyendo la tasa de crecimiento por la expresión de la ecuación 36 se obtiene:
Cuando la tasa de reinversión es cero, la ecuación queda reducida a:
Debido a que G = πn,t captura, en términos nominales, el efecto inflación sobre capital invertido, y en términos reales el crecimiento es nulo porque la reinversión no existe. El modelo supone: i) flujos de fondos reales constantes a perpetuidad, ii) flujos de fondos nominales no constantes a perpetuidad, aumentando a razón de la tasa de inflación (π) , por el revalúo del capital invertido. Al especificar la tasa de crecimiento de esta manera hace que el modelo sea neutral a la inflación, obteniendo la siguiente igualdad20:
Si las inversiones proyectadas generan un rendimiento igual al costo del capital el modelo se conoce como Zero Net Present Value Investment (ZNPI), en donde las inversiones marginales tienen VAN = 0. Incorporando la expresión tasa de crecimiento (ecuación 36) nuevamente se obtiene:
Este se reduce a la siguiente expresión 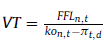 , consistente a valores reales y nominales, a partir de las ecuaciones 33 y 34.
, consistente a valores reales y nominales, a partir de las ecuaciones 33 y 34.
2.7. Descuento de flujos de fondos: valuación en dos monedas, proyecciones en moneda de cierre e inicial
Las PTI y PPC (ecuaciones 1 a 5) brindan el marco consistente para valuar en moneda doméstica (d) y extranjera (x) de cierre e inicio. Para ello existen dos caminos:
a) Conversión de flujos nominales en moneda local a flujos nominales en moneda extranjera: se parte de los flujos de fondos proyectados estimados en la ecuación 25. Primero se debe proyectar la evolución del tipo de cambio futuro. Para ello se utiliza la curva de rendimientos estimada para cada periodo (ecuación 1) (Hull, 2005; López Dumrauf, 2014b). Seguidamente, los flujos nominales (FFL t,n ) son convertidos a moneda extranjera empleando el tipo de cambio futuro (F t,n ), para obtener los flujos nominales en moneda extranjera (FFL xt,n ), así:
Luego los flujos nominales (ecuación 41) se actualizan al CCPP nominal en moneda extranjera. El CCPP nominal extranjero (kox n,t ) se obtiene a partir del CCPP nominal doméstico (ecuación 3), así:
Referente al valor actual en moneda extranjera (VA x ) este es:
b) Conversión de flujos reales en moneda local a flujos reales en moneda extranjera: el insumo son los flujos reales domésticos (ecuación 27). Primero se debe estimar el tipo de cambio futuro real (F t,r ). Para ello se calcula el tipo de cambio futuro nominal (ecuación 1), y luego se ajusta por la inflación extranjera y se deflacta por la doméstica, así:
Adicionalmente, el flujo en moneda extranjera en moneda inicial (FFL xt,r ) es:
Por otra parte, el CCPP (ecuación 44) es deflactado para obtener el CCPP en términos reales (kox r,t ), así:
Actualizando los flujos en moneda inicial con el CCPP real se llega al mismo valor que en términos nominales:
El proceso asegura que el valor en moneda doméstica (VA d ), dividido el tipo de cambio spot sea igual al valor actual en moneda extranjera.
A la inversa, el valor en moneda extranjera multiplicado por el tipo de cambio spot es igual al valor actual en moneda doméstica.
3. Metodología. Análisis de caso de valuación en dos monedas de empresa en marcha
Se utiliza la metodología del estudio de casos21 ya que no se pretende establecer soluciones generalizables estadísticamente. En tal sentido, en este apartado será utilizado un caso de estudio que complementa e ilustra el modelo integral desarrollado en la sección precedente. Como unidad de análisis fue utilizada una empresa del tipo pequeña-mediana que opera y funciona en un mercado emergente como el sistema económico argentino. Dado lo anterior, se pretende determinar su valor intrínseco a través del modelo de descuento de flujo de fondos, trabajando las variables en términos nominales y reales, expresando valores en moneda local y extranjera. De esta forma, la primera moneda es el peso argentino y la segunda el dólar estadounidense. A continuación se desarrolla el caso respetando la secuencia lógica planteada en la figura 1.
a) Proyección de las variables macro: tasas de interés, inflación y tipo de cambio:
Suponiendo que las relaciones de Fisher se sostienen, la primera tarea a desarrollar consiste en proyectar las tasas esperadas de interés doméstica y extranjera. No se debe perder de vista que Argentina se caracteriza por tener un mercado de capitales emergentes, en consecuencia no se encuentran disponibles bonos cupón cero, ni STRIPS o americanos que abarquen el horizonte de proyección de 6 años. Descartada la técnica de bootstrapping, se opta por la estimación de la curva logarítmica de rendimientos. Para esto se usaron los datos correspondientes a la duración modificada y TIR de bonos soberanos en moneda doméstica22 y dólares estadounidenses publicados por el Instituto Argentino de Mercados de Capitales (IAMC), referenciadas en las tablas A2 y A3 del anexo.
En tal sentido, las curvas obtenidas para la proyección de las tasas son: i) TIR pesos argentinos: -0,064ln(x) + 0,2283; ii) TIR dólares: 0,0104ln(x) + 0,0402; -212,6ln(x) + 1.618,18. Se debe tener presente que el ajuste logarítmico fue empleado en la proyección de la inflación local (Π t,d) (ecuación 3). Por lo tanto, primero se calculó la curva por ajuste logarítmico correspondiente a la inflación extranjera (Π t,e) utilizando datos correspondientes a la inflación promedio anual de Estados Unidos desde el año 1999- 2016 (Agosto)23. La tabla 1 presenta los resultados obtenidos para las tasas esperadas, tipo de cambio esperado (ecuación 1), inflacióndoméstica esperada a partir de la inflación extranjera (ecuación 3) y efecto Fisher internacional (ecuación 6).
Tabla 1 Tasas de interés proyectadas E(i d ), E(i x ); tipo de cambio futuro nominal F t,n ; tasa de inflación proyectada Π t,e , Π t,d ; tasa real suponiendo equilibrio de Fisher
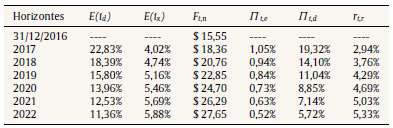
Fuente: elaboración propia.
b) Proyección de ingresos, costos, resultados operativos y flujos de fondos:
Con los valores obtenidos en la tabla 1 se construyen los coeficientes para expresar las magnitudes financieras en moneda de cierre o nominal (ecuaciones 9,10 y 11) e inicial o real (ecuaciones 12,13 y 14). Para las proyecciones es definido un horizonte explícito de cuatro periodos. Los valores resultantes de las proyecciones de unidades vendidas, producidas, precios, ingresos totales, costos variables, costos fijos y existencias finales e iniciales de bienes de cambio en moneda de cierre e histórica son expuestos en la tabla A4 del anexo (ecuaciones 17 a 20). El detalle correspondiente al impuesto a las ganancias proyectado (ecuación 21), resultados operativos después de impuestos proyectados (ecuación 22) y la inversión incremental en capital de trabajo (ecuaciones 23 y 24) son expuestos en la tabla A5 del anexo, donde las cifras se expresan en miles de pesos argentinos. La tabla 2 presenta los flujos proyectados nominales (ecuación 25), y los flujos en términos reales (ecuaciones 16 y 26).
Tabla 2 Flujos de fondos proyectados nominales (moneda de cierre) y reales (iniciales) (en miles)
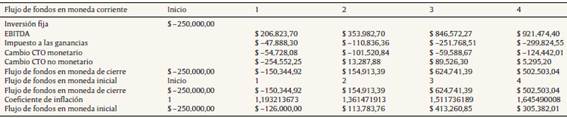
Fuente: elaboración propia.
c) Estimación del costo del capital en términos nominales y reales:
Uno de los insumos para estimar el CCPP es la tasa de rendimiento requerido por los propietarios, o costo del capital propio. Para ello se empleó el clásico modelo CAPM adaptado a mercados emergentes. En este caso se utilizó el modelo G-CAPM (Global CAPM) ajustado por riesgo país, propuesta ampliamente difundida y utilizada por los practicantes24. La tasa de costo de capital propio se estimó en dólares estadounidenses. Como proxy de la tasa libre de riesgo (r f ) se utilizó el promedio aritmético 1928-2016 correspondiente a T-Bonds, y en el mismo sentido el adicional por riesgo de mercado, a partir del promedio aritmético de la diferencia entre el índice S&P500 y T-Bonds25. El coeficiente beta (β i) se obtuvo a partir del beta sectorial desapalancado para el sector retail, correspondiente a países emergentes, siendo βu = 0,855726. Para su apalancamiento, se le incorporó la estructura capital objetivo de la firma (D = 30%; E = 70%) y se supuso deuda no riesgosa27. Finalmente, se incorporó el adicional por riesgo país (Country Risk Premium, CR) con base en el modelo de Damodaran (2015); arrojando un adicional del 586 puntos básicos para el año 201728. Obtenida la tasa de rendimiento requerido en dólares estadounidenses (E(r i,US$)), este se convierte a pesos domésticos E(r i) empleando la ecuación 42. En dicha estimación son empleadas las tasas de inflación proyectadas para Argentina y Estados Unidos (ecuaciones 7 y 8). Los valores desagregados de los componentes integrantes del costo del capital propio son expuestos en la tabla 3.
Tabla 3 Estimación tasa de rendimiento requerida (k e )
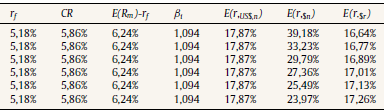
Fuente: elaboración propia con base en los datos del sitio http://www.stern.nyu.edu/∼adamodar/pc/datasets
La tabla 3 constituye un paso previo para obtener el CCPP nominal (ecuación 30), el CCPP real directo (ecuación 31) e indirecto (ecuación 32) expresado en pesos. Los valores obtenidos para el CCPP son expuestos en la tabla 4. En este caso se supuso como tasa de deuda en términos nominales aquella que se cobra para empresas de primera línea. Por lo tanto, obtenido el CCPP nominal se deriva la tasa real del costo de capital (ecuación 7).
Tabla 4 Proyección del CCPP expresado en términos nominales y reales
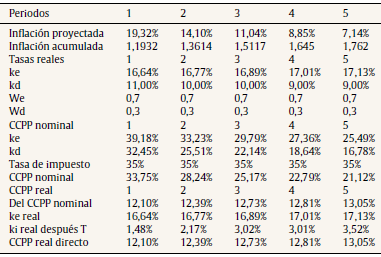
Fuente: elaboración propia.
En la tabla 5 se presentan los valores relativos al CCPP en dólares, empleando las ecuaciones 42 y 46.
Tabla 5 Proyección del CCPP en dólares en términos nominales y reales

Fuente: elaboración propia.
d) La determinación del valor de continuidad (valor terminal):
En la tabla 6 se presentan las variables utilizadas y los resultados obtenidos en la estimación del valor de continuidad. Se supone que el comportamiento de los flujos de fondos en T-1 (año 4) se estabiliza en T (año 5), momento definido como horizonte de continuidad. En la tabla 6 se presentan los resultados de los modelos: (i) ZRGM en moneda de cierre e inicial (A y B) (ecuaciones 38 y 39); (ii) ZNPIM nominal con crecimiento equivalente (C) y crecimiento mayor (D) (ecuación 40) a la inflación. En ZNPI las inversiones incrementales generan un VAN = 0.
Tabla 6 Determinación del valor de continuidad ZRGM y ZNPI (miles)
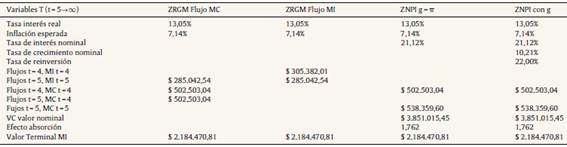
Fuente: elaboración propia.
En todos los casos queda demostrado que los modelos son neutrales a la inflación, y consistentes en su formulación, ya que arrojan el mismo valor.
e) Determinación del valor actual en moneda doméstica y extranjera, en términos nominales y reales:
Las tablas precedentes son las piezas necesarias para armar el modelo propuesto en la figura 1. Por lo tanto, las variables estimadas en moneda local, nominales y reales son convertidas en flujos nominales y reales expresados en dólares futuros. Las tablas empleadas como insumo son: tabla 1 que provee los valores de i) tasas de interés proyectadas local y extranjera; ii) inflación esperada local y extranjera; iii) tipo de cambio futuro. Tablas 4 y 5 de donde se obtiene el CCPP nominal para Argentina y Estados Unidos. De esta forma, la tabla 7 expone los valores correspondientes al tipo de cambio proyectado peso-dólar (ecuación 1), nominal deflactado (ecuación 16) y real proyectado (ecuación 44).
Tabla 7 Tipo de cambio futuro nominal, deflactado y real
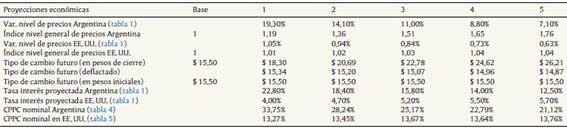
Fuente: elaboración propia.
Las variables de la tabla 7 son las que permiten la conversión de los flujos de fondos proyectados nominales en pesos a dólares, aplicando la ecuación 43. Para convertir el costo del capital a dólares se utilizó la ecuación 42. Finalmente, el valor actual en dólares se obtiene aplicando la ecuación 43. Los flujos expresados en pesos de poder adquisitivo de inicio son convertidos a dólares utilizando el tipo de cambio futuro real (ecuación 45). El CCPP extranjero real y el valor actual (ecuaciones 46 y 47) son expuestos en la tabla 8.
Tabla 8 Valor actual flujo de fondos nominales y reales en dólares estadounidenses
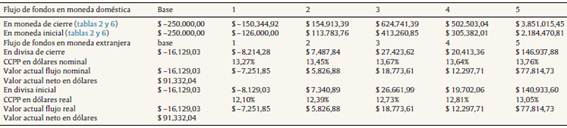
Fuente: elaboración propia.
f) Consistencia entre valor actual en moneda local y extranjera: Los resultados obtenidos demuestran la congruencia del modelo y la clave reside en plantear las proyecciones de tasas de interés, inflación esperada y tipo de cambios desde las teorías de paridad (PTI, PPC). A esto debe sumarse la correcta especificación de las variables que definen el descuento de flujo de fondos en contextos inflacionarios: proyección de magnitudes financieras, costo del capital y valor terminal, respetando técnicamente los efectos absorción y traslación.
La tabla 9 expone los valores correspondientes a los flujos en términos reales y nominales, así como su valor actual en pesos, ratificando la consistencia del enfoque con el valor estimado en dólares. Con las ecuaciones 48 y 49 se obtiene que el cociente entre el valor en pesos dividido el tipo de cambio spot ($1.415.646,61/$15,50) arroja un resultado de US$91.332,04 y viceversa.
Tabla 9 Valor actual flujos de fondos nominal y real en pesos

Fuente: elaboración propia.
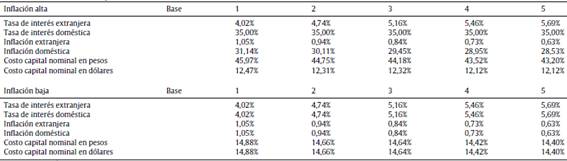
Como complemento se realizó un análisis de escenarios, suponiendo dos extremos de inflación (alto y bajo) con el fin de observar la sensibilidad de las variables del modelo ante diferentes niveles de inflación y el valor de la firma. Se supusieron tasas de interés nominal directamente vinculadas con los escenarios, por ser estas los insumos primarios para el cálculo de la inflación, tipo de cambio y coeficientes. En el escenario de alta inflación se supone una tasa de interés doméstica constante del 35%; para el escenario de baja inflación se supone que la tasa de interés local es similar a la proyectada para Estados Unidos. La tabla 10 presenta los resultados correspondientes a las principales variables del modelo, mientas que el valor del costo del capital promedio ponderado en ambas monedas, tasas de interés e inflación doméstica y extranjera se presenta en la tabla A6 del anexo.
Tabla 10 Escenarios alta-baja inflación y valor de la firma
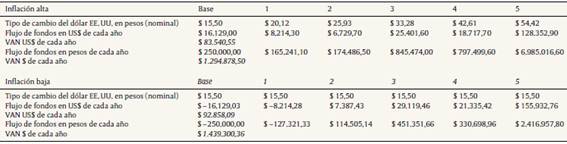
Fuente: elaboración propia.
La variación relativa obtenida de comparar los valores de la firma correspondientes a los escenarios y el resultado del caso base indica que, en contextos de baja inflación, la variación es del 1,67%. Para niveles de alta inflación en términos absolutos asciende al 9%. Si bien estos resultados no son concluyentes, se observa la relación negativa valor-inflación, en parte como resultado del aumento exponencial del factor de actualización, si se lo compara con el incremento que experimentan los valores de las proyecciones financieras. El comportamiento inverso se observó en contextos de baja inflación, donde se presentó un menor impacto en la reducción del factor de descuento.
4. Conclusiones
En el presente artículo se plantea como objetivo explicitar una secuencia lógica de valuación mediante el método de descuento de flujos de fondos en contextos inflacionarios. El modelo procura obtener resultados consistentes en moneda local y extranjera, como consecuencia de aplicar las teorías de la paridad, en las proyecciones de magnitudes financieras en moneda de cierre (nominal) e inicial (real). Apoyado en un importante cuerpo de publicaciones relativas al tema, se propuso una secuencia lógica de trabajo. El punto de partida, y al mismo tiempo principal sostén del modelo, lo constituyen las teorías de la paridad. Sobre la base de las anteriores, se desarrollaron las consideraciones técnicas para el tratamiento de magnitudes financieras proyectadas, tasas de costo del capital, valor terminal y conversión de valores monetarios en moneda local a moneda extranjera.
El modelo cumple con el objetivo de brindar coherencia lógica en el valor estimado en moneda doméstica y extranjera, puesto que el punto de partida reside en la aplicación de las teorías de paridad y la consistencia de los efectos absorción y traslación en los flujos y tasas. El simple ejercicio de escenarios desarrollado en la parte final arroja como resultado una relación negativa y asimétrica entre el valor intrínseco del descuento de flujos de fondos y los niveles de inflación. Adicionalmente, se puede atribuir un sesgo negativo pronunciado en procesos de alta inflación, propio del comportamiento exponencial e incremental del factor de descuento.
Conflicto de intereses
Los autores declaran no tener ningún conflicto de intereses.
Notes
1 En la tabla A1 del anexo se incluye un listado de abreviaciones que se emplearán en el documento, esto con el fin de facilitar su lectura.
2 De aquí en adelante será empleada la acepción nominal para las variables monetarias que incorporan la inflación esperada o poder adquisitivo futuro. La terminología real se reserva para aquellas variables expresadas en poder adquisitivo de origen o inicio. Se consideran sinónimo de nominal la palabra moneda de cierre y en el caso de real moneda de inicio.
3 Si un litro de leche cuesta $1 (unidades monetarias extranjeras) en el extranjero, en el mercado doméstico debería costar lo mismo en términos de divisas. Si en el extranjero el índice de inflación esperada es del 3% y en la economía doméstica es del 7%, se espera que el tipo de cambio se aprecie en términos nominales (en el caso contrario, se espera que la moneda doméstica se deprecie en términos nominales) a razón de (1,07/1,03) = 3,88%. En ese caso el precio del litro de leche en unidades de moneda extranjera mantiene el valor en el mercado local, producto de la paridad en el poder de compra.
4 Irving Fisher planteó el hecho de que las tasas nominales de interés reflejan la expectativa colectiva inflacionaria, y que dicha tasa compensa a los agentes de los efectos negativos de la inflación sobre el rendimiento real de sus inversiones (Fisher, 1965).
5 Si se parte de una tasa de interés real 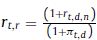 ; despejando en función de la tasa nominal se tiene r
t,d,n
= r
t,r
+ π
t,d
+ (r
t,r
× π
t,d
), or
t,d,n
= r
t,r
+ π
t,d
(1 + r
t,r
). La anterior expresión indica que la tasa nominal varía en función a las expectativas inflacionarias, sin perjuicio que la tasa real se mantenga constante. De esta forma, se tendría para dos periodos de tiempo r
d,n,1
– r
d,n,0
= r
t,r
+ π
d,1
(1 + r
r
) − r
r
+ π
d,0
(1 + r
r
) y reagrupando términos r
d,n,1
– r
d,n,0
= ( π
t,1
– π
t,0
) × (1 + r
r
). Consecuentemente, al variar la tasa de inflación de un periodo a otro, la tasa nominal se debe modificar proporcionalmente, para que la tasa real se mantenga constante.
; despejando en función de la tasa nominal se tiene r
t,d,n
= r
t,r
+ π
t,d
+ (r
t,r
× π
t,d
), or
t,d,n
= r
t,r
+ π
t,d
(1 + r
t,r
). La anterior expresión indica que la tasa nominal varía en función a las expectativas inflacionarias, sin perjuicio que la tasa real se mantenga constante. De esta forma, se tendría para dos periodos de tiempo r
d,n,1
– r
d,n,0
= r
t,r
+ π
d,1
(1 + r
r
) − r
r
+ π
d,0
(1 + r
r
) y reagrupando términos r
d,n,1
– r
d,n,0
= ( π
t,1
– π
t,0
) × (1 + r
r
). Consecuentemente, al variar la tasa de inflación de un periodo a otro, la tasa nominal se debe modificar proporcionalmente, para que la tasa real se mantenga constante.
6 En mercados emergentes, el no cumplimiento de las condiciones precedentes hace que no exista una oferta de títulos con distintos vencimientos y torna dificultosa su implementación.
7 STRIPS es un acrónimo de Separated Trading of Registered Interest and Principal of Securities. En esencia son bonos cupón cero que nacen de un bono principal o nota, siendo estos los cupones de los primeros. El acto de separar el cupón del bono principal, y negociarlos en el mercado se conoce como stripping. Desde ese momento, los cupones (STRIPS) pasan a ser bonos y su rendimiento es la diferencia entre el valor de compra y el valor de mercado a fecha de venta o el nominal si son mantenidos en cartera hasta el vencimiento.
8 Por ejemplo, un bono bullet con vencimiento a tres semestres (1,5 años), 5% cupón anual, tasas spot para el primer y segundo semestre de 2% y 2,125%. Si no se conoce la tasa en el tercer periodo, entonces $100 = $2, 5(1 + 0, 2)–1 + $2, 5(1 + 0, 02125)–2 + $102, 5(1 + i3)–3, se procede a descontar el valor del cupón $95, 15 = $102, 5(1 + i 3 )–3 y se despeja en función de la tasa i 3 = 0, 0251. Se utiliza otro bullet con vencimiento a 2 años (cuatro semestres) y se completa las tasas con los datos anteriores: spots observadas (i 1 , i 2 ), estimada mediante bootstrapping (i 3 ) y nuevamente se despeja (i 4 ).
9 La duración (duration) a menudo se la asocia con el tiempo, en el sentido del plazo de recuperación de la inversión comprometida en el bono. En realidad, la medida representa el centro de gravedad de los pagos del bono, ya que los pondera por el tiempo y su participación en el valor actual del título. La duración modificada es un coeficiente para establecer el cambio en el precio del bono ante un cambio en el tipo de interés, para cambios pequeños, suponiendo relación lineal precio-tasa. La convexidad es la segunda derivada de la curva precio-tasa y mide la reacción en el precio del bono ante cambios de mayor magnitud en su TIR.
10 Se emplea la curva logarítmica debido a que esta es la que mejor ajusta a la relación duración modificada-TIR, ya que al aumentar la duración el crecimiento de la TIR es rápido al principio para luego suavizarse frente a mayores duraciones (López Dumrauf, 2014a).
11 Nótese que la ecuación anterior mide el cambio en precios relativos pronosticados, a diferencia de la ecuación 9, donde se analiza la evolución nominal de un precio.
12 Respecto del costo del capital los tres métodos empleados son (Ruback, 2002; Damodaran, 2006; Booth, 2007; Fernández, 2014): a) Costo capital promedio ponderado (CCPP o WACC por sus siglas en inglés de Weighted average cost of capital); b) Flujos de fondos a capital; c) Valor presente ajustado (APV, por su sigla en inglés). En el presente trabajo se adoptará la técnica del CCPP.
13 No es el objetivo del presente trabajo indagar sobre las técnicas prospectivas utilizadas en la proyección de estados financieros. Sin perjuicio de ello, la metodología de mayor difusión está dada por el uso de la técnica de escenarios (Miller y Waller, 2003; Wright, Cairns y Goodwin, 2009; Esandi, Milanesi y Pesce, 2012).
14 En rigor las existencias iniciales a valores históricos equivalen a las existencias finales del periodo anterior.
15 Cabe aclarar que, suponiendo que en el año de determinación se liquida el impuesto y este se paga en dicho ejercicio, el anticipo de impuesto genera un activo corriente monetario con resultado negativo por exposición a la inflación.
16 Positivo en el caso de que los pasivos monetarios sean superiores a los activos monetarios, y negativo en el caso inverso.
17 En el caso de trabajar con moneda inicial (ecuación 27) se debe prestar atención al tratamiento del impuesto a las ganancias y el capital de trabajo: a) Impuesto a las ganancias: las cifras se expresan en moneda de poder adquisitivo inicial, tanto ventas como costo de artículos vendidos. Se debe incorporar el resultado por la inflación en ingresos (EI t = IT t,n – IT t,r ;efecto positivo) y costos (EC t = CMV t,n – CMV t,r ; efecto negativo), en el último caso para incorporar en la base imponible el incrementos de los valores por los productos comprados, las existencias finales e iniciales en cada periodo se computan en moneda de poder adquisitivo inicial. Las amortizaciones e ingresos por venta de bienes de uso se computan en moneda inicial, consecuentemente el impuesto determinado es equivalente al estimado en moneda de cierre, IT t,r – CMV t,r + E It – EC t – A t,r – IVAF t,r = BI × T. El impuesto determinado se deflacta (ecuación 15). b) Capital de trabajo: se debe expresar el resultado por exposición a la inflación en el flujo de fondos (ecuación 27) y este surge de la diferencia entre la variación total y real del capital de trabajo monetario: ΔCTM (total)t,n – ΔCTM (real)t,r = REI t .
18 La TIR en términos reales no se estima directamente a partir de la nominal, ya que esta medida es una tasa promedio y por lo tanto la nominal promedia la inflación de todo el periodo. Debe calcularse a partir de los flujos reales. Una medida alternativa a la TIR, que mitiga sus defectos, es la conocida como tasa interna de retorno promedio o TIRP (Magni, 2013; Milanesi, 2016). Muchos de los problemas de la TIR se subsanan con la TIRP, entre ellos la posibilidad de aplicar la paridad de Fisher para derivar la TIRP real.
19 En este caso se verifica una sobreestimación del valor del CCPP y subestimación del valor de la firma, ya que el ahorro fiscal se calcula sobre intereses nominales (Modigliani y Cohn, 1984). La diferencia en la tasa de CCPP entre el procedimiento correcto e incorrecto es  .
.
20 Esto es así ya que si en la ecuación 38 el denominador ko n,t – π n,t se sustituye por [kor,t + πt,d + kor,t × πt,d]− π t,d , operando se reduce a ko r,t (1 + π t,d ). Seguidamente, los coeficientes de capitalización a inflación esperada (1 + π t,d ) en el numerador y denominador se simplifican.
21 El estudio de casos como metodología de investigación no debe confundirse con el análisis o estudio de casos como herramienta pedagógica, la cual busca analizar un aspecto concreto relacionado con las organizaciones para fomentar el debate o discusión (Castro Monge, 2010). En este caso se busca analizar el funcionamiento de proposiciones teóricas con el fin de ampliar o generalizar una teoría (Yin, 1994).
22 El rendimiento de los bonos indexados por el coeficiente de estabilización de referencia (CER) fue ajustado por una inflación proyectada del 17% para el primer año, conforme los datos oficiales plasmados en la ley de presupuesto nacional para el ejercicio 2017 (ver Ministerio de Hacienda y Finanzas Pública, Presidencia de la Nación Argentina http://www.economia.gob.ar/).
23 Obtenida del sitio www.us.inflator.calculator.com arrojando una curva y = –212,6ln(x) + 1.618,8.
24 En relación con el CAPM, son conocidas las limitaciones que presenta, en particular para estimar tasas de rendimiento requerido en contextos emergentes; una excelente revisión actualizada del tema se puede ver en Fama y French (2004). En lo que respecta a soluciones empleadas por los profesionales para estimnar tasas de rendimiento que reflejen los riesgos de emergentes, existe una importante cuerpo literario, entre los que se puede citar a Copeland et al. (2000); Fornero (2003); Damodaran (2006); Pratt y Grabowski (2008); Damodaran (2009).
25 Los datos fueron extraídos del sitio elaborado por A. Damodaran, Discount rate estimation, Annual returns on stock, bonds and t-bills 1928-current. http://www.stern.nyu.edu/∼adamodar/pc/datasets/histretSP.xls
26 Los datos fueron extraídos del sitio elaborado por A. Damodaran, Discount rate estimation, Total beta by sector, Emerging. http://www.stern.nyu.edu/∼adamodar/pc/datasets/betas.xls
27 El apalancamiento de βu se realizó con la clásica ecuación βi = βu × (1 + D (1 − t) /C.
28 Los datos son obtenidos del sitio de A. Damodaran, correspondiente al riesgo país depurado de riesgo crediticio, http://people.stern.nyu.edu/adamodar/New_Home_Page/datafile/ctryprem.html
Bibliografía
Argandoña, A. (2013). Irvin Fisher: un gran economista (I. B. Navarra, Ed.). Working Paper WP-1082 (IESE insight 11/2013), pp. 1-44 [consultado 2 Oct 2016]. Disponible en: Disponible en: http://www.iese.edu/research/pdfs/WP-1082.pdf
Booth, L. (2007). Capital cash flow, APV and valuation. European Financial Management, 13(1), 29-48.
Bradley, M. y Gregg, J. (2008). Expected inflation and the constant growth valuation model. Journal of Applied Corporate Finance, 20(2), 66-78.
Brealey, R., Myers, S. y Allen, F. (2006). Principles of corporate finance (8 th ed.). Boston: McGraw Hill Primis.
Castro Monge, E. (2010). El estudio de casos como metodología de investigación y su importancia en la dirección y administración de empresas. Revista Nacional de Administración, 2(1), 31-54.
Copeland, T., Koller, T. y Murrin, J. (2000). Valuation: Measuring and managing the value of companies (3 rd ed.). New York: Wiley.
Damodaran, A. (2006). Damodaran on valuation (2 nd ed.). New York: John Wiley & Sons.
Damodaran, A. (2009). Volatility rules: Valuing emerging market companies. Working Paper [consultado 17 May 2017]. Disponible en: Disponible en: http://people.stern.nyu.edu/adamodar/pdfiles/papers/emergmkts.pdf
Damodaran, A. (2015). Country risk: Determinants, measures and implications. Social Science Research Network (SSRN) [consultado 17 May 2017]. Disponible en: Disponible en: https://documents.tips/documents/ssrn-id2630871pdf.html
Emery, D. y Finnerty, J. (2007). Corporate financial management (3 rd ed.). New Jersey: Prentice Hall.
Esandi, J., Milanesi, G. y Pesce, G. (2012). Análisis de escenario y opciones reales: un caso de aplicación para empresas de base tecnológica. XXXII Jornadas Sociedad Argentina de Docentes en Administración Financiera SADAF, 63-82 [consultado 17 May 2017]. Disponible en: Disponible en: http://www.sadaf.com.ar/espanol/publicaciones/publicacion_individual.php?id=212
Fabozzi, F. y Fabozzi, D. (1996). Bond Markets, analysis and strategies. New Jersey: Prentice Hall.
Fama, E. y French, K. (2004). The capital asset pricing model: Theory and evidence. Journal of Economics Perspectives, 18(3), 25-46.
Fernández, P. (2014). Valoración de empresas y sensatez (3.a ed.). Barcelona: IESE Business School-Universidad de Navarra.
Fisher, I. (1965). The theory of interest. New York: August Kelley.
Fornero, R. (2003). Finanzas de empresas en mercados emergentes. XXIII Jornadas de Sociedad Argentina de Docentes en Administración Financiera SADAF, 107-125 [consultado 4 Mar 2017]. Disponible en: Disponible en: http://www.sadaf.com.ar/espanol/publicaciones/publicacion_individual.php?id=212
Gordon, M. (1962). The investment, financing and valuation of the corporation. Illinois: Irwin Homewood.
Hull, J. (2005). Futures, options and other derivatives (5 th ed.). New Jersey: Prentice Hall .
López Dumrauf, G. (2014a). Análisis cuantitativo de bonos (1.a ed.). Buenos Aires: Alfaomega.
López Dumrauf, G. (2014b). Currency choice in valuation: An approach for emerging markets. The Business and Economics Research Journal, 7(1), 11-22.
Magni, C. (2013). The internal rate of return approach and the AIRR paradigm: A refutation and a corroboration. The Engineering Economist, 58(2), 73-111.
Milanesi, G. (2016). La Tasa interna de retorno promedio borrosa: desarrollos y aplicaciones. Journal of Economics, Finance and Administrative Science, 21, 39-47.
Miller, K. y Waller, G. (2003). Scenarios, real options and integrated risk management. Journal of Long Range Planning, 36(1), 93-107.
Modigliani, F. y Cohn, R. (1984). Inflation and corporate financial management. MIT Sloan School Working Paper, pp. 1-37 [consultado 4 Mar 2017]. Disponible en: Disponible en: http://mitsloan.mit.edu/faculty-and-research/academic-groups/work-andorganization-studies/publications-and-working-papers/
Pratt, S. y Grabowski, R. (2008). Cost of capital: applications and examples (3 rd ed.). New Jersey: John Wiley & Sons.
Rappaport, A. (1998). Creating shareholder value (2 nd ed.). New York: The Free Press.
Ruback, R. (2002). Capital cash flow: A simple approach to valuing risky cash flow. Financial Management, 31(2), 85-103.
Tham, J. y Velez Pareja, I. (2011). Will the deflated WACC please stand up? And the Real WACC should sit down. Cuadernos Latinoamericanos de Administración, 6(12), 1-17.
Titman, S. y Grinblatt, M. (2002). Financial markets and corporate strategy. New York: McGraw-Hill.
Velez Pareja, I. (2006). Valoración de flujos de caja en inflación. El caso de la regulación en el Banco Mundial. Academia. Revista Latinoamericana de Administración, 36, 24-49.
Wright, G., Cairns, G. y Goodwin, P. (2009). Teaching scenario planning: Lessons from practice in academe and business. European Journal of Operational Research, 194(1), 323-335.
Yin, R. (1994). Case study research: Design and methods. Thousand Oaks, CA: Sage Publications.
Tabla A1 Listado de abreviaciones empleadas en el documento

Fuente: elaboración propia.
Tabla A2 Bonos soberanos nominados en pesos
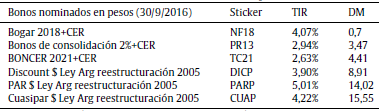
Fuente: elaboración propia a partir de la información del Instituto Argentino de Mercado de Capitales.
Tabla A3 Bonos soberanos nominados en dólares
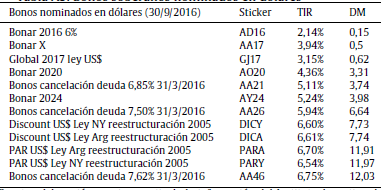
Fuente: elaboración propia a partir de la información del Instituto Argentino de Mercado de Capitales.
Tabla A4 Proyección unidades ventas-producción, precios, costos unitarios, ingresos totales, costos totales y existencias en moneda de cierre
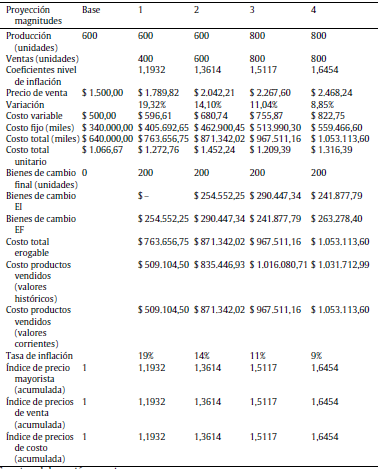
Fuente: elaboración propia
Tabla A5 Proyección resultados operativos, determinación del impuesto a las ganancias y capital de trabajo
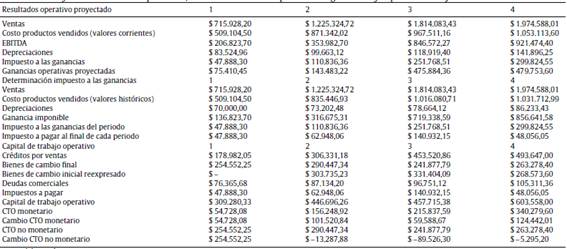
Fuente: elaboración propia
Tabla A6 Variables empleadas en la simulación
Fuente: elaboración propia