CONSTANT LEVERAGE AND CONSTANT COST OF CAPITAL: A COMMON KNOWLEDGE HALF-TRUTH

IGNACIO VÉLEZ–PAREJA1, RAUF IBRAGIMOV2, JOSEPH THAM3

1Ingeniero Industrial, M. Sc. en Ingeniería Industrial. Profesor Asociado, Universidad Tecnológica de Bolívar, Cartagena, Colombia. ivelez@unitecnologica.edu.co, nachovelez@gmail.com

2Matemático, Ph.D en Ciencias (Candidato), Maestría en Administración. Profesor asociado, Graduate School of Finance and Management, Moscow, Russia. ibrauf@rambler.ru

3Matemático, EdD, Harvard University. Profesor asistente visitante, Duke University - Duke Center for International Development, Estados Unidos joseph.tham@duke.edu

First version: June 29, 2007

This version: July 8, 2008

Fecha de recepción: 21-04-2008 Fecha de corrección: 20-05-2008 Fecha de aceptación: 29-05-2008

ABSTRACT

A typical approach for valuing finite cash flows is to assume that leverage is constant (usually as target leverage) and the cost of equity, Ke and the Weighted Average Cost of Capital, WACC are also assumed to be constant. For cash flows in perpetuity, and with the cost of debt, Kd as the discount rate for the tax shield, it is indeed the case that the Ke and WACC applied to the FCF are constant if the leverage is constant. However this does not hold true for finite cash flows.

In this document we show that for finite cash flows, Ke and hence WACC depend on the discount rate that is used to value the tax shield, TS and as expected, Ke and WACC are not constant with Kd as the discount rate for the tax shield, even if the leverage is constant. We illustrate this situation with a simple example. We analyze five methods: DCF using APV, FCF and traditional and general formulation for WACC, present value of CFE plus debt and Capital Cash Flow, CCF.

KEY WORDS

WACC, constant cost of capital, constant leverage, cash flows.

Clasificación JEL: D61, G31, H43

RESUMEN

Un enfoque típico para valorar flujos de caja finitos es suponer que el endeudamiento es constante (generalmente como un endeudamiento objetivo o deseado) y que por tanto, el costo del patrimonio, Ke y el costo promedio ponderado de capital CPPC, también son constantes. Para los flujos de caja perpetuos, y con el costo de la deuda, Kd como la tasa de descuento para el ahorro en impuestos o escudo fiscal, Ke y el CPPC aplicado al flujo de caja libre FCL son constantes si el endeudamiento es constante. Sin embargo esto no es verdad para los flujos de caja finitos.

En este documento mostramos que para flujos de caja finitos, Ke y por lo tanto el CPPC dependen de la tasa de descuento que se utiliza para valorar el ahorro en impuestos, AI y según lo esperado, Ke y el CPPC no son constantes con Kd como la tasa de descuento para el ahorro en impuestos, aunque el endeudamiento sea constante. Ilustramos esta situación con un ejemplo simple. Analizamos cinco métodos: el flujo de caja descontado, FCD, usando APV, el FCD y la formulación tradicional y general del CPPC, el valor presente del flujo de caja del accionista, FCA más deuda y el flujo de caja de capital, FCC.

PALABRAS CLAVE

Costo promedio ponderado de capital, CPPC, costo de capital constante, endeudamiento constante, flujos de caja.

INTRODUCTION

In this document we show that using the findings of Tham and Velez-Pareja (2002), for finite cash flows, Ke (cost of levered equity) and hence WACC (Weighted Average Cost of Capital), depend on the discount rate that is used to value the tax shield (TS), and as expected, Ke and WACC are not constant with Kd (cost of debt) as the discount rate for the tax shield, even if the leverage is constant. We illustrate this situation with a simple example. We analyze five methods: DCF Discounted Cash flows (the Free Cash Flow, FCF) using APV, FCF and traditional and general formulation for WACC, present value of Cash Flow to equity (CFE) plus debt and Capital Cash Flow (CCF).

A typical approach for project or firm valuation which could be found in practice (See for example World Bank (2002), Benninga (1997, 2006), Brealey and Myers (2000, 2003), Brealey, Myers and Allen (2006), Copeland, Koller and Murrin (1995, 2000) is to discount cash flows expected within the finite time horizon at constant cost of capital, (usually as a target leverage) assuming that target leverage is maintained throughout the life of the project, and thus its cost of levered equity Ke and the WACC are constant. Though it might be convenient to perform calculations under such assumption, it is not in fact always true that Ke and WACC are constant under the constant leverage financing policy. As could be seen from the findings and example of Inselbag and Kaufold (1997), and as a general expression for Ke and WACC derived by Tham and Velez-Pareja (2002), both the cost of levered equity and the Weighted Average Cost of Capital depend on the value of the interest tax shield (VTS), and in the case of finite cash flows valuation, they could be changing from period to period if certain choice is made for the rate to discount expected tax shields.

The case of variable leverage has been studied elsewhere by Mian and Velez Pareja (2008), Velez-Pareja (2004, 2005), Velez-Pareja and Burbano (2006), Velez-Pareja and Tham (2001, 2004, 2006a, 2006b), and Tham and Velez Pareja (2002, 2004). In these cases, they find complete consistency between all methods and with different assumptions about the discount rate for the tax shields.

Practitioners frequently assume that the risk (and corresponding discount rate, ψ) of the interest tax shield is the cost of debt, Kd. This is done explicitly when, for example, the APV method is applied, or implicitly, if popular formula Ke= Ku + (Ku-Kd)×(1-T)×D/E (Ku, the cost of unlevered equity; T, corporate tax rate; D and E are market values of debt and equity, respectively) is used to estimate the cost of equity capital. As Taggart (1991) and Tham and Velez-Pareja (2002, 2004) prove, this formulation is valid only for a fixed (in perpetuity) dollar amount of debt, thus under constant leverage assumption it could be applied only to perpetual cash flows. However, this formula is used by Fernandez (2002), Shapiro (2005) and others even within finite planning horizon and when dollar amount of debt is changing from period to period. Another example of implicit ψ = Kd assumption is applying Hamada’s formulation to unlever and relever betas. Initially developed by Hamada (1972) for flat perpetuity and risk free debt, his formula is persistently used in conjunction with discounting at constant WACC under constant leverage assumption,1 potentially producing significant valuation errors as can be seen from the comprehensive example analyzed by Mian and Velez-Pareja (2008). Velez-Pareja and Tham (2004, 2006a, 2006b) repeatedly show that, if assumptions and formulae are mismatched, inconsistencies arise when calculating value with different methods. So analysts should be very careful dealing with finite cash flows. To obtain correct and consistent valuation results one should specify assumption for the risk of the tax shield (ψ) first, and from that assumption choose the proper formulation for Ke and WACC.

Different values one proposes for ψ, the risk or discount rate for the TS might be questioned based on the particular debt policy and underlying expectations for the cash flow profile. However, when selecting the assumption or approach for ψ, we have to be consistent in the use of the formulation for the cost of capital. If under the constant leverage financing policy the risk ψ of the interest tax shield is assumed2 to be equal to Kd, then Ke and WACC could not be assumed constant. Put it another way, ψ = Kd and constant Ke and WACC are incompatible assumptions within the constant leverage set up.

To illustrate the scenario of non constant cost of capital with constant leverage3 we present a simple example, and analyze five DCF methods:

  1. Adjusted present value (APV);
  2. Discounting FCF at WACC calculated from the traditional formulation;
  3. Discounting FCF at WACC calculated from the general formulation;4
  4. Cash flow to equity (CFE) discounted at the cost of levered equity plus the value of debt, and
  5. Capital Cash Flow (CCF) discounted at the corresponding cost of capital.

The rest of the document is organized as follows: in Section Two, we present the generalized formulation for the cost of capital for the finite cash flow valuation, and in particular formulae under the assumption that the discount rate for the tax shield (TS) is Kd. In Section Three we show a simple example. In Section Four we conclude.

1. GENERAL FORMULATION FOR KE AND WACC

Taggart (1991) presents a revision of the set of formulations for the cost of levered Ke and WACC for perpetuities and finite cash flows. He introduces the formulation with and without personal taxes and for different level of risk for discounting the TS, including the Miles and Ezzell (1980). However, Taggart does not include the case of ψ = Kd for finite cash flows. Inselbag and Kaufold (1997) include the formulation of Ke and WACC for the case of Kd, the cost of debt as the level of risk for the TS and finite cash flows, but neither Taggart (1991) nor Inselbag and Kaufold (1997) show the formulation for the cost of capital appropriate to discount capital cash flow (CCF) under ψ = Kd and finite cash flows scenario.

Tham and Velez-Pareja (2002) present a derivation of the general expression for Ke, the cost of levered equity for different levels of ψ corresponding to the risk of the tax shields, and resulting formulations for the general WACC, which should be applied to discount the Free Cash Flow (FCF) and Capital Cash Flow (CCF) both for finite time horizon valuation and for perpetuities.

The general formulation for Ke is,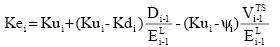

Where Ku is the unlevered cost of equity, ψ is the risk (discount rate) of the TS, D is market value of debt, E is market value of equity and VTS is the market value of TS; i is the period of analysis.

The general formulation for WACCFCF is,

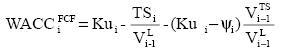
where TS is tax savings, VL is the market value of the levered firm and the other variables were defined above.

Following the path of the classic WACC derivation, we can easily show that general expression for the classic WACC is

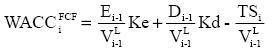
and we obtain traditional formula

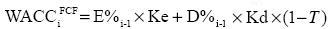
when TSi = Kd×Di-1×T.

The general formulation for the WACCCCF is

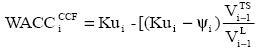
The general formula for the value of TS is

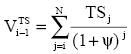
When the risk of TS, ψ, is Ku, then Ke simplifies to

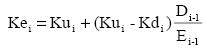
This formulation is valid for finite cash flows or perpetuities.

The WACC for the FCF simplifies to

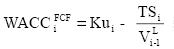
When taxes are paid when accrued and there is enough EBIT to earn the TS, then WACCFCF is

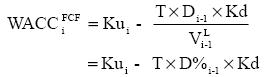
And the WACC for the CCF simplifies to

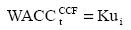
The value of the TS is

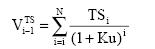
When the risk of TS, ψ, is Kd, then Ke simplifies to

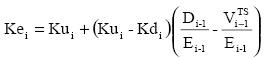
for finite cash flows and

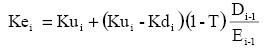
for perpetuities.

The WACC for the FCF simplifies to

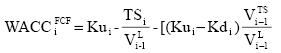
for finite cash flows.

And the WACC for the CCF simplifies to

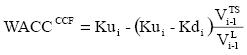
The value of the TS is

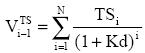
Observe that in the case of ψ = Ku, Ke does not depend on TS and does not depend on the value of TS. Instead, when ψ = Kd, Ke depends on TS and the value of TS. On the other hand, when ψ = Ku, WACC depends on TS and it will be constant when taxes are paid when accrued and there is enough EBIT to earn the TS. Instead, when ψ = Kd, WACC depends on TS and the value of TS.

From these formulations we can conclude that for finite cash flows leverage and cost of capital are constant when:

  1. There is enough EBIT to fully earn the TS.
  2. Taxes are paid when accrued.
  3. The risk of TS is Ku.
  4. Tax rate T, is constant.
  5. Interest rate on debt is equal to the (market) cost of debt, Kd.

With this set of formulations we can illustrate with a simple numerical example that Ke and WACC are not constant when leverage is maintained constant if one assumes Kd (or any other value different from Ku) to be the appropriate discount rate for the expected interest tax shields. This can be seen in the formulation for Ke and WACC.

Full consistency in valuation results could be obtained for all five methods we mentioned in the Introduction if proper formulation for the cost of capital is applied to discount corresponding cash flow.

2. SIMPLE EXAMPLE

A typical approach for valuing finite cash flows is to assume that leverage is constant and hence, Ke and WACC are introduced as constant. In this document, we show that using the findings of Tham and Velez-Pareja (2002), Ke, and hence WACC, depends on the value of the tax shield, TS, and as expected, Ke and WACC are not constant when we assume the risk of TS as Kd. We illustrate this situation with a simple example. We analyze five methods:

  1. APV;
  2. DCF using FCF and traditional formulation for WACC;
  3. DCF using FCF and general formulation for WACC;
  4. Present value of CFE plus debt, and
  5. Capital Cash Flow, CCF discounted at the WACC for CCF.

In the Appendix, the reader will find the complete information and the financial statements.

Assume a project (or the firm) with the following information:

  1. Some input data.
  2. Income Statement, Cash Budget and Balance Sheet.
  3. Cash flows derived from the financial statements.

Assume that the input data is as in Table 1.

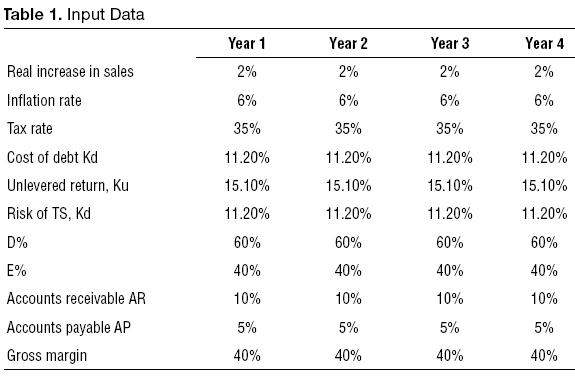
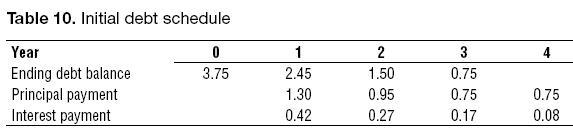
Sales start with $10 in year 1. The fixed assets cost $4. The expected ending balance for the initial debt is shown in Table 2.

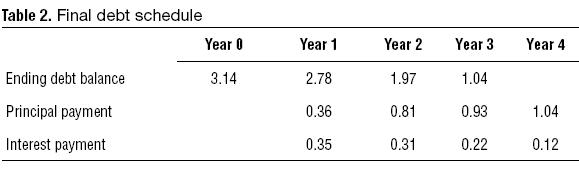
The complete financial statements are shown in the Appendix. From the financial statements we derive the following cash flows:

  1. Free Cash Flow, FCF.
  2. Cash Flow to Debt, CFD.
  3. Cash Flow to Equity, CFE.
  4. Tax savings.

Now we calculate the working capital for each year.

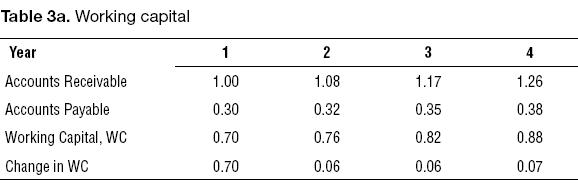
With the change in working capital we can construct the FCF using the indirect method.

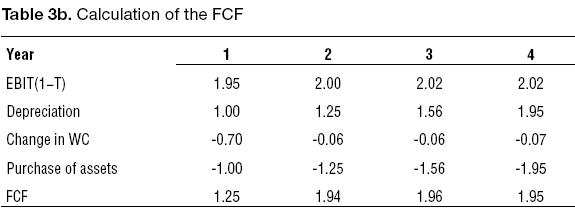
We show the different cash flows in the next table.

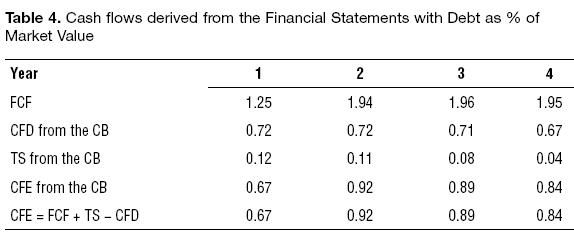
With this information we can perform the valuation of the cash flows. In the next tables we show the valuation for each method after solving the iteration process to solve the circularity between value and discount rate, where necessary.

Using the APV and assuming that the discount rate for the TS is Kd:

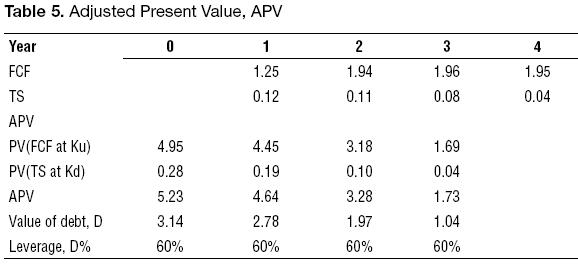
Using the DCF, the traditional WACC, and assuming that the discount rate for the TS is Kd:

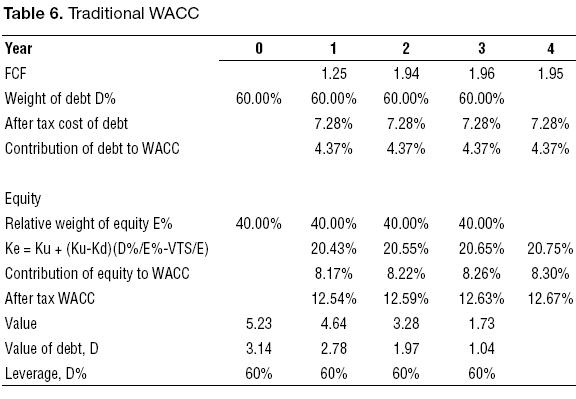
Observe that Ke and WACC are not constant. This occurs because the Ke is a function of the value of TS.

Using the DCF, the general WACC, and assuming that the discount rate for the TS is Kd:

Using the CFE and assuming that the discount rate for the TS is Kd:

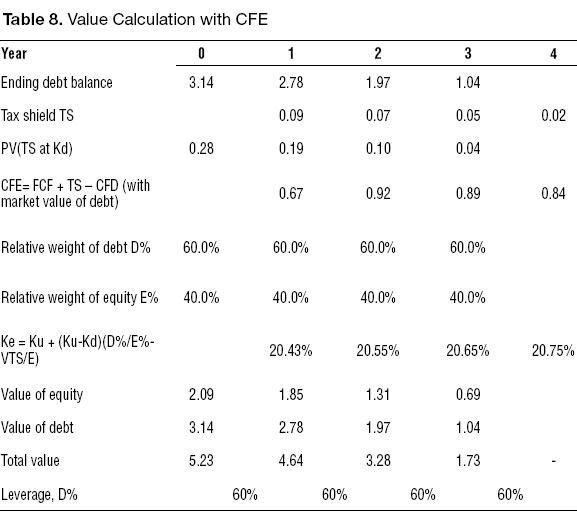
And finally, using the CCF with the WACCCCF , and assuming that the discount rate for the TS is Kd:

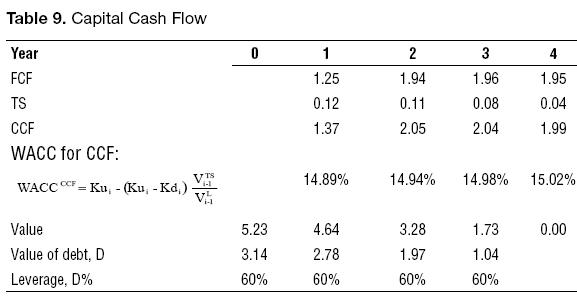
Observe that the WACCCCF is not constant even if we assume that Ku is constant. WACCCCF is constant and equal to Ku (assuming no change in the operating risk for the firm and constant inflation) when we assume that the discount rate for the TS is Ku. The reason is identical to the one that makes Ke and WACCFCF non constant when leverage is constant and we assume the risk of TS equal to Kd: Ke, WACCFCF and WACCCCF depend on the value of TS.

As we have shown, first of all, all methods match5 when we use the proper formulation for the cost of capital (Ke and WACC); second, we have shown that the constant leverage does not mean that Ke and WACC are constant. Tham and Velez-Pareja (2002, 2005), and Velez-Pareja and Tham (2006a, 2006b) have shown that when using Ku as the risk for the TS and some conditions regarding the payment of taxes, the existence of enough EBIT to earn the TS and the source of the TS, the cost of capital is constant.6

Observe that the value calculated assuming ψ equal to Kd is higher than the value when we assume that ψ equal to Ku. A question arises here: is it reasonable to think that, changing the financing policy from constant leverage to predetermined debt schedule (non constant leverage), the firm will increase its value? We leave the answer to this question for another work.

Now we can check the difference between the initial debt schedule and the new debt schedule based on the market value of debt.

The new debt schedule is shown in next table.

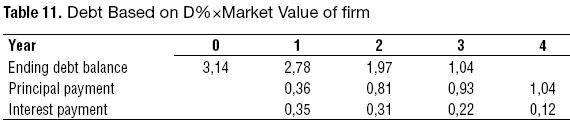
This means that management has to adjust debt from the beginning in order to achieve the target leverage. The difference in debt level is as follows.

3. SUMMARY AND CONCLUDING REMARKS

We have shown that a constant leverage does not grant that the cost of capital is constant when the risk of the TS is Kd. Moreover, in order to achieve a proper valuation of finite cash flows with a constant leverage when the risk of TS is Kd, we have to use some formulations that differ from the traditional used by practitioners and textbooks. In other words, assuming constant leverage is not a sufficient condition to have constant cost of capital. We need to make explicit assumptions on the risk for the TS and use formulation for the cost of capital that is consistent with the assumed risk of the tax shield. Using the proper formulation in this scenario, we obtain full consistency in the calculation of value. This means that there are no advantages of one method over another. All of them give the same value (when properly done) and all of them (even the APV) require iterations when the risk of the TS is Kd.

In short, we can conclude that for finite cash flows leverage and cost of capital are constant when:

  1. There is enough EBIT to fully earn the TS.
  2. Taxes are paid when accrued.
  3. The risk of TS is Ku.
  4. Tax rate T, is constant.
  5. Interest rate on debt is equal to the (market) cost of debt, Kd.

In addition, we have to be aware that performing cash flow valuation with constant Ke and WACC under constant leverage assumption implies that particular formulations must be used for the estimation of Ke. Since the possibility of constant leverage and constant cost of capital scenario arises only when ψ = Ku, analysts should use formula

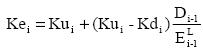
to calculate the cost of levered equity directly, and formula

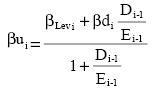
or

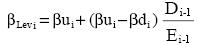
for unlevering and levering the beta in case they use the CAPM. Here βu and βLev are the unlevered and levered β’s and Dt-1 and Et-1 are the market values of debt and equity.

When we assume that the risk of the TS is Kd, we cannot assume constant WACC or Ke because leverage is constant. The formulations for Ke and WACC (either for the Free Cash Flow, FCF or the Capital Cash Flow, CCF) depend not only on the constant leverage, but on the value of the TS and that refrains the cost of capital from being constant even if leverage is constant.

Summary of results assuming Kd as the risk of the TS, Table 13.

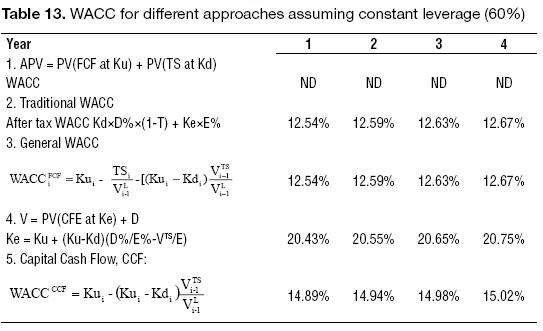
In the case of the risk for the TS equal to Ku, we can observe the equations for Ke, WACC for the FCF and the CCF, as follows:

The general formulation for Ke is,

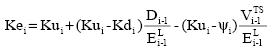
When the risk of the TS is Ku, the third term of the RHS of the equation vanishes and Ke depends only on Ku, Kd and leverage (constants). Hence, Ke is constant.

The general formulation for WACCFCF is,

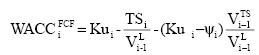
When the risk of the TS is Ku, the third term in the previous equation vanishes and the second term is T×Kd×D% and hence WACCFCF depends only on leverage which is constant. Hence, WACC is constant.

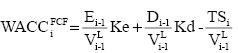
In this case, if Ke is constant then WACCFCF is constant.

The general formulation for the WACCCCF is

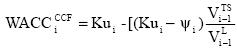
When the risk of the TS is Ku, the second term of the RHS of the equation vanishes and WACCCCF = Ku which is a constant.

FOOTNOTES

1. Here we can mention very different texts from practitioners and academics: Pratt, Reilly and Schweihs (2000), Abrams (2001), Damodaran (2002),

2. This assumption is by itself debatable

3. Which for example could be achieved through debt rebalancing at the end of every period to keep constant its percentage of the estimated project value)

4. See Tham and Velez-Pareja (2002, 2004).

5. This is a matching of identical results. We have tested it for more than 10 decimals and the difference is strictly, zero. The interested reader might receive the spreadsheet upon request to the authors.

6. We are assuming that EBIT≥0. When this condition is not met, the traditional expression for WACC is no longer valid. When this happens we should use equation (4) and as can be seen from it, WACC might not be constant (imagine that there is not TS earned during some period). When TS is not earned, WACC for the FCF is just Ku.

BIBLIOGRAPHY

Abrams, J.B. (2001). Quantitative Business Valuation: A Mathematical Approach for Today’s Professional. New York, NY: McGraw-Hill.

Benninga, S.Z. (2006). Principles of Finance with Excel. New York, NY: Oxford University Press.

Benninga, S.Z., & Oded, H.S. (1997). Corporate Finance. A Valuation Approach. New York, NY: McGraw- Hill.

Brealey, R. & Myers, S.C. (2000). Principles of Corporate Finance (6th ed.). New York, NY: McGraw Hill-Irwin.

Brealey, R. & Myers, S.C. (2003). Principles of Corporate Finance (7th ed.). New York, NY: McGraw Hill-Irwin.

Brealey, R., Myers, S.C., & Allen, F. (2006). Principles of Corporate Finance (8th ed.). New York, NY: McGraw Hill-Irwin.

Copeland, T.E., Koller, T. & Murrin, J. (1995). Valuation: Measuring and Managing the Value of Companies (2nd ed.). New York, NY: John Wiley & Sons.

Copeland, T.E., Koller, T. & Murrin, J. (2000). Valuation: Measuring and Managing the Value of Companies (3rd ed.). New York, NY: John Wiley & Sons.

Damodaran, A. (2002). Investment Valuation: Tools and Techniques for Determining the Value of Any Asset (2nd ed.). New York, NY: John Wiley & Sons.

Fernandez, P. (2002). Valuation Methods and Shareholder Value Creation. San Diego, CA: Academic Press.

Hamada, R.S. (1972). The Effect of the Firm’s Capital Structure on the Systematic Risk of Common Stock. Journal of Finance, 27(2), 435-452.

Inselbag, I. & Kaufold, H. (1997, Spring). Two DCF Approaches in Valuing Companies under Alternative Financing Strategies (and How to Choose between Them). Journal of Applied Corporate Finance, 10(1), 114-122.

International Bank for Reconstruction and Development – The World Bank. (2002). Financial Modeling of Regulatory Policy [CD set].

Mian, M.A. & Velez-Pareja, I. (2008). Applicability of the Classic WACC Concept in Practice. Latin American Business Review, 2(8). Available at SSRN: http://ssrn.com/abstract=804764

Miles, J. & Ezzell, J.R. (1980). The Weighted Average Cost of Capital, Perfect Capital Markets, and Project Life: A Clarification. Journal of Financial and Quantitative Analysis, 15, 719-730.

Pratt, S.P., Reilly, R.F. & Schweihs, P. (2000). Valuing A Business: The Analysis and Appraisal of Closely Held Companies (4th ed.) New York, NY: McGraw-Hill.

Shapiro, A.C. (2005). Capital Budgeting and Investment Analysis. Upper Saddle River, NJ: Pearson Prentice Hall.

Taggart, R.A., Jr. (1991). Consistent Valuation and Cost of Capital Expressions with Corporate and Personal Taxes. Financial Management, 20(3), 8-20.

Tham, J. & Velez–Pareja, I. (2002). An Embarrassment of Riches: Winning Ways to Value with the WACC (SSRN Working Paper 352180). Available at: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=352180

Tham, J. & Velez-Pareja, I. (2004). Principles of Cash Flow Valuation. An Integrated Market Approach. London: Academic Press.

Tham, J. & Velez–Pareja, I. (2005). Modeling Cash Flows with Constant Leverage: A Note (SSRN Working Paper 754444). Available at: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=754444

Velez-Pareja, I. (2004). Modeling the Financial Impact of Regulatory Policy: Practical Recommendations and Suggestions. The Case of World Bank (SSRN Working Paper 580042). Available at: http://ssrn.com/abstract=580042

Velez-Pareja, I. (2005). Cash Flow Valuation in an Inflationary World: The Case of World Bank for Regulated Firms. (SSRN Working Paper 643266). Available at: http://ssrn.com/abstract=643266

Velez–Pareja, I. & Burbano, A. (2006). Consistency in Valuation: A Practical Guide (SSRN Working Paper 758664). Available at: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=758664

Velez–Pareja, I. & Tham, J. (2001). A Note on the Weighted Average Cost of Capital WACC (SSRN Working Paper 254587). Available at: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=254587

Velez-Pareja, I. & Tham, J. (2004). Consistency in Chocolate. A Fresh Look at Copeland’s Hershey Foods & Co Case (SSRN Working Paper 490153). Available at: http://ssrn.com/abstract=490153

Velez–Pareja I. & Tham, J. (2006a). Constant Leverage Modeling: A Reply to "A Tutorial on the McKinsey Model for Valuation of Companies (SSRN Working Paper 906786). Available at: http://ssrn.com/abstract=906786

Velez-Pareja, I. & Tham, J. (2006b). The Mismatching of APV and the DCF in Brealey, Myers and Allen 8th Edition of Principles of Corporate Finance, 2006 (SSRN Working Paper 931805). Available at: http://ssrn.com/abstract=931805

Velez–Pareja I. & Tham, J. (2006c). Valuation of Cash Flows with Constant Leverage: Further Insights (SSRN Working Paper 879505). Available at: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=879505