Caso de estudio

DOI: 10.1016/j.estger.2017.06.004

Análisis envolvente de datos. Un caso de estudio para una universidad argentina

Data envelopment analysis. A case study for one Argentinian university

Análise envoltória de dados. Um estudo de caso para uma universidade Argentina

a Profesora Adjunta, Departamento de Matemática, Universidad Nacional del Sur, Bahía Blanca, Argentina

b Profesor titular, Departamento de Economía, Universidad Nacional del Sur, Bahía Blanca, Argentina

c Investigador Principal, Instituto de Matemática de Bahía Blanca, CONICET, Bahía Blanca, Argentina

* Autor para correspondencia. Avenida Alem 1253, CP (8000), Bahia Blanca, Argentina. Correo electrónico: fvillarreal@uns.edu.ar (F. Villarreal).

Recibido el 30 de septiembre de 2016
Aceptado el 20 de junio de 2017
On-line el 26 de agosto de 2017

Resumen

Este artículo presenta un caso de estudio en el que se analiza la eficiencia relativa del plan de estudios de un programa universitario. Esta cuestión es muy relevante, ya que los cursos del plan están financiados con fondos públicos y por lo tanto afectan la eficiencia del gasto público global. El método aplicado es el análisis envolvente de datos (DEA, por sus iniciales en inglés). Los resultados permiten identificar los cursos optativos ineficientes que deberían aumentar el número de estudiantes y reducir al mismo tiempo el número de miembros del cuerpo docente asignados a ellos para mejorar su eficiencia. En el caso de cursos obligatorios, la mejora también requiere reducir el número de docentes auxiliares.

Palabras clave: Análisis envolvente de datos. Modelos de optimización. Educación universitaria.

Códigos JEL: C61. I23.

Abstract

This article presents a study case in which we analyze the relative efficiency of the curriculum of a university degree program. This is a relevant question, since the required courses are publicly funded and thus affect the efficiency of global public spending. The method applied is Data Envelopment Analysis (DEA). Through the our results, we were able to identify inefficient non-mandatory courses that should increase the number of students while reducing the number of faculty members assigned to them to improve their efficiency. In the case of mandatory courses, improvement also requires to reduce the number of adjunct faculty.

Keywords: Data envelopment analysis. Programming models. Higher education.

JEL classifications: C61. I23.

Resumo

Este artigo apresenta um estudo de caso em que a eficiência relativa do currículo de um programa universitário é analisada. Esta questão é muito relevante porque os cursos do plano são de financiamento público e, portanto, afetam a eficiência da despesa pública global. O método aplicado é a análise envoltória de dados (DEA, por sua sigla em Inglês). Os resultados permitem identificar eletivas ineficientes que deveriam aumentar o número de alunos e, ao mesmo tempo, reduzir o número de membros do corpo docente que lhes foram atribuídos para melhorar a sua eficiência. No caso de cursos obrigatórios, a melhoria também requer reduzir o número de assistentes de ensino.

Palavras-chave: Análise envoltória de dados. Modelos de otimização. Educação universitária.

Classificações JEL: C61. I23.

1. Introducción

La evaluación del desempeño y mejora de la eficiencia de las entidades educativas no es particular de Argentina sino que ha cobrado una importancia creciente hace más de dos década a nivel mundial. Así lo reflejan los trabajos de Rhodes y Southwick (1993) y Ahn, Charnes y Cooper (1988) en Estados Unidos, el de Sarrico, Hogan, Dyson y Athanassopoulos, 1997 en el Reino Unido y el de Marinho, Resende y Façanha (1997) y Bandeiras (2000) en Brasil, por mencionar algunos.

En el caso de las instituciones que proveen educación superior, el interés por esta cuestión radica principalmente en el hecho de que se financian, total o parcialmente, con fondos públicos y, por lo tanto, la eficiencia en el uso de esos fondos afecta a la eficiencia global del gasto público.

La dificultad para establecer una función de producción a nivel educativo que combine inputs y outputs en una agregación con valor económico hace necesaria la utilización de métodos no paramétricos para evaluar la eficiencia en este sector. Entre este tipo de métodos cuantitativos se encuentra el análisis envolvente de datos (DEA, por su sigla en inglés).

El objetivo de este trabajo es evaluar la eficiencia relativa de los cursos o asignaturas que comprenden el plan de estudio de una carrera universitaria identificando entre ellas cuáles son las ''unidades eficientes'' y las ''relativamente ineficientes'', en qué se diferencian y qué medidas de gestión se sugiere implementar para la mejora continua de su desempeño. El interés por esta cuestión radica especialmente en que estos cursos se financian con fondos públicos y, por lo tanto, la eficiencia en el uso de esos fondos afecta a la eficiencia global del gasto público. El modelo DEA empleado fue el de Banker, Charnes y Cooper (BCC) output orientado.

Este trabajo cuenta con 6 secciones adicionales a esta introducción. En la segunda sección se realiza una revisión de la literatura; en la tercera se presenta el caso de estudio; en la cuarta sección se presenta la metodología utilizada; en la quinta, los resultados obtenidos; en la sexta, las consideraciones finales, y en la última sección se plantean las preguntas de discusión sobre el caso de estudio analizado.

2. Revisión de la literatura

Es importante tener presente que ''el concepto de eficiencia más pertinente en el ámbito escolar es el de eficiencia técnica, que indica el grado de aprovechamiento técnico de los recursos puestos al servicio de la producción educativa'' (Ventura Blanco, 1999, p. 56).

De acuerdo con Coria (2011), en la literatura económica pueden encontrarse distintas metodologías para evaluar la eficiencia técnica de las unidades de producción. Todas ellas se basan en la resolución propuesta por Farrell (1957) para cuantificar la eficiencia técnica de un conjunto de unidades productivas, es decir, en la construcción empírica de una función de producción representativa de las mejores prácticas productivas a partir de una serie de datos que representan los insumos y los productos implicados en el proceso productivo. Las metodologías se diferencian en su carácter paramétrico o no (según se establezca o no una forma funcional particular para la función de producción) y en su carácter determinístico o estocástico (según identifiquen toda la desviación como ineficiencia o no).

En el ámbito de ''la educación superior'', la evaluación de la eficiencia se ha realizado a través del cálculo de indicadores. Ortiz (2003) mide la eficiencia de un conjunto de carreras de Ingeniería de una universidad nacional aplicando un indicador de eficiencia, el cual es inversamente proporcional a las pérdidas totales que el mismo registre. El autor concluye que existe una alta ineficiencia en las carreras analizadas según los resultados que arroja el indicador calculado. Becerra, Cetrángolo, Curcio y Jiménez (2003) en un trabajo sobre el gasto público universitario en Argentina, analizan la eficiencia y asignación del presupuesto de las universidades de gestión estatal, así como la diversidad existente entre las instituciones, a través de algunos indicadores relacionados con la cantidad de egresados, la relación entre esa cantidad y la de ingresantes y el gasto medio por alumno. Los autores encuentran que el sistema universitario de gestión estatal es ineficiente, lo cual se manifiesta en los elevados índices de abandono, el alargamiento de la duración media de las carreras y de las bajas tasas de graduación en comparación con otros países de la región'' (Coria, 2011, p. 47).

La dificultad para establecer una función de producción a nivel educativo que combine inputs y outputs en una agregación con valor económico y hace necesaria la utilización de métodos no paramétricos para evaluar la eficiencia en este sector. Entre este tipo de métodos cuantitativos se encuentra el DEA (Ventura Blanco, 1999).

En este sentido, ''la metodología DEA permite manejar múltiples insumos y productos y expresarlos en cualquier unidad de medida, siempre y cuando los mismos tipos de productos e insumos mantengan su homogeneidad en todas las productivas. La posibilidad de considerar procesos de producción multiproducto es la razón fundamental por la cual la metodología ha sido utilizada para evaluar la eficiencia de las instituciones educativas. Otra ventaja del método es que permite calcular la eficiencia en sectores caracterizados por la ausencia de precios, razón por la cual es muy utilizado para evaluar la eficiencia del sector público. Por último, el método ofrece información sobre las unidades productivas analizadas, como la ponderación de insumos y productos, lo que puede ser de utilidad desde la perspectiva de la gestión. Asimismo, por ser una técnica no paramétrica, posibilita calcular la eficiencia sin hacer supuestos sobre la relación funcional entre insumos y productos'' (Coria, 2011, p. 52). Entre las principales aplicaciones de la metodología DEA, fuera del ámbito educativo, se encuentran los trabajos sobre evaluación de eficiencia de las distintas unidades productivas de una entidad pública de fiscalización y control de sanidad y calidad agroalimentaria (Alberto y Curchod, 2011), evaluación de la eficiencia relativa en hoteles españoles (Alberca y Parte, 2013), evaluación de la eficiencia relativa de los bancos comerciales de Brasil (Maçada, 2001), evaluación de la eficiencia relativa en equipos de atención primaria de salud (Legaz, 1998), entre otros. En el ámbito educativo, Sarrico y Dyson (2000), Kao y Hung (2008), Kuah y Wong (2011) y Coria (2011) aplican la metodología DEA.

En Argentina, si bien la metodología DEA ha sido utilizada para medir la eficiencia dentro del sistema universitario, no hay trabajos relacionados con la evaluación de la eficiencia de los cursos en un plan de estudios universitario. De aquí la importancia de presentar este caso de estudio aplicando esta metodología para evaluar la eficiencia relativa de los cursos en un plan de estudios universitario, identificando las ''unidades eficientes'' y las ''relativamente ineficientes'', mostrando en qué aspectos se diferencian y sugiriendo medidas de gestión para la mejora del desempeño de las últimas.

3. Caso de estudio

En el año 1956, la Universidad Nacional del Sur (Argentina) se estructura en ocho departamentos, uno de los cuales, el de Contabilidad, es en la actualidad el Departamento de Ciencias de la Administración. El programa de Contador Público es una las carreras de pregrado que en él se dictan y en la actualidad se encuentra en el proceso de acreditación. Su plan de estudio ha ido sufriendo distintas modificaciones conforme la dinámica sociedad-economía lo ha exigido, a fin de que el perfil de la carrera permita al graduado enfrentar con éxito los distintos cambios.

El plan de estudios vigente entre los años 2006-2009 constaba de una formación básica de dos años y de un ciclo profesional a partir del tercer año. Dada la estructura departamental de la universidad, las materias de las áreas de Matemática, Economía y Derecho no son de responsabilidad del Departamento de Administración. Así, de las 32 asignaturas que componían el plan solo 28, entre optativas y obligatorias, fueron dictadas por docentes que pertenecen al departamento; la carga horaria de cada una fue de 6 horas, siendo la asistencia a la misma no obligatoria y el régimen de cursado cuatrimestral, dictándose en un solo cuatrimestre, primero o segundo, según fuese la exigencia de correlatividades. Las materias optativas son elegidas libremente por el estudiante según sea la orientación que haya elegido en cuanto a su formación profesional y en las postrimerías de su carrera.

A los fines de este trabajo, cada una de estas 28 asignaturas se ha tomado como unidad operativa. De esta forma, se ha analizado la información correspondiente al año 2009, en donde se utilizó como fuente secundaria de datos la Memoria Anual del departamento.

En este sentido, se pretende evaluar la eficiencia relativa de las 28 asignaturas o cursos efectuando una comparación objetiva de su desempeño mediante modelación matemática, a fin de detectar cuáles son los factores que hacen que unas sean más o menos eficientes que otras. El concepto de eficiencia es definido tomando como base la definición de Charnes, Cooper y Rhodes (1981) como una razón entre la suma ponderada de sus outputs (productos generados) y la suma ponderada de sus inputs (recursos), relativos a cada una de las unidades de análisis. Con base en esto, la eficiencia se considera como la capacidad que tiene cada asignatura de, a partir de sus recursos (profesores, auxiliares, personal de apoyo), producir su máximo ''producto'' relativo a la enseñanza (Bandeiras, 2000).

4. Metodología

DEA es una técnica no-paramétrica determinística que recurre a la programación matemática y que surge a raíz de la tesis doctoral de Rhodes (1978). Desde que en el año 1978 fue publicado en la revista European Journal of Operational Research por Charnes, Cooper y Rhodes el primer trabajo aplicando DEA, el desarrollo de esta metodología, tanto en el ámbito teórico como en el de aplicación empírica a problemas del mundo real, ha crecido considerablemente (Gómez, 2016).

Su objetivo es evaluar la eficiencia relativa de un conjunto de n Decision Making Units (DMU) o sistemas (S_j) de producción de bienes o servicios homogéneos entre sí, en el sentido de que a partir de las mismas entradas produzcan el mismo tipo de resultados. Dichos sistemas transforman una serie de ''m'' entradas en una serie de ''s'' salidas. Si m y s son iguales a 1 –es decir, una única entrada y salida–, la eficiencia relativa de cada sistema j puede evaluarse como la simple relación entre la cantidad de su única salida y la cantidad de su única entrada, es decir:

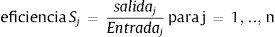(1)

Cuando se quieren evaluar n sistemas con más de una entrada y más de una salida, la expresión de la eficiencia debería consignarse como el cociente entre la suma ponderada de las salidas y la suma ponderada de las entradas. En este caso hay que definir los pesos de cada salida y cada entrada definidos como u_r y v_i.

Estos pesos de cada salida y cada entrada pueden fijarse por criterios técnicos, en general subjetivos, y una vez se han fijado se los utiliza para evaluar la eficiencia relativa de todas las unidades o sistemas. No obstante, el método DEA proporciona otra forma de estimar estos pesos relativos, determinando para cada sistema j los pesos que resulten más apropiados, de tal forma que ubica al sistema j en la mejor posición posible en comparación con los otros sistemas evaluados. DEA proporciona una estimación individual de los valores u_r y v_i para cada unidad a partir de los datos disponibles, formulando un modelo de programación matemática cuyas variables de decisión son justamente los u_r y v_i. Esta forma de estimar los pesos relativos resulta completamente objetiva y sus valores pueden variar de una unidad a otra.

A continuación, en las subsecciones 4.1 y 4.2 se presentan las características de los modelos básicos DEA Charnes, Cooper y Rhodes (DEA-CCR) y DEA-BCC. Se debe tener presente que la clasificación de estos modelos se realiza en función de la orientación del modelo y la tipología de los rendimientos a escala (Coll y Blasco, 2006).

4.1 Modelo básico de Charnes, Cooper y Rhodes

De acuerdo a la orientación del modelo, la eficiencia puede ser caracterizada con relación a dos orientaciones básicas, definiéndose los siguientes modelos:

• Modelo orientado al input: dado el nivel de outputs, busca la máxima reducción proporcional en el vector de inputs mientras permanece en la frontera de posibilidades de producción.
• Modelo orientado al output: dado el nivel de inputs, busca el máximo incremento proporcional de los outputs permaneciendo dentro de la frontera de posibilidades de producción.

Teniendo en cuenta esta clasificación, una unidad será considerada eficiente solo cuando no sea posible incrementar las cantidades de output manteniendo fijas las cantidades de inputs utilizadas, ni sea posible reducir las cantidades de inputs empleadas sin alterar las cantidades de outputs obtenidas.

En cuanto a la clasificación de los modelos de acuerdo a su rendimiento, se debe tener presente que los rendimientos de escala reflejan la respuesta del producto total cuando todos los factores se incrementan proporcionalmente. En este sentido, se pueden encontrar los siguientes tipos de rendimientos asociados a estos modelos:

• Modelo de rendimientos contantes de escala: se presenta cuando la cantidad utilizada de todos los factores y la cantidad obtenida de producto varían en la misma proporción.
• Modelo de rendimientos crecientes: sucede cuando al variar la cantidad utilizada de todos los factores en una determinada proporción, la cantidad obtenida del producto varía en una proporción mayor.
• Modelo de rendimientos de escala decrecientes: se presenta cuando al variar la cantidad utilizada de todos los factores en una proporción determinada, la cantidad obtenida de producto varía en una proporción menor.

En este orden de ideas, el modelo DEA-CCR proporciona medidas de eficiencia proporcional, con orientación input u output, de rendimientos a escala constantes.

El modelo DEA-CCR es un modelo de programación matemática no lineal que plantea una función objetivo que maximiza la eficiencia de una unidad o sistema genérico (S_j) para el que se desea determinar los pesos u_r y v_i de los inputs y outputs considerados. Por lo tanto, el modelo resultante tiene la siguiente estructura de programación no lineal:

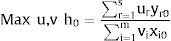(2)

Sujeto a: ∑_r=1^su_ry_rj / ∑_i=1^mv_ix_ij ≤1 j = 1,2,...n ur,vi≥ 0

Donde x_ij (x_ij ≥ 0) representa las cantidades del input i (i = 1,2,...,m) consumidos por la j-ésima unidad e y_rj (y_ij ≥ 0) representa las cantidades observadas del output r (r = 1,2,...,s) producidos por la j-ésima unidad.

Para determinar la eficiencia de cada unidad funcional se deben resolver n modelos, uno para cada unidad o sistema. De esta forma, ''si la solución óptima es h₀ = 1, esto indicará que la unidad que está siendo evaluada es eficiente en relación con las otras unidades. Si h₀ < 1, la unidad será ineficiente'' (Coll y Blasco, 2006, p. 34).

Adicionalmente, cada modelo no lineal puede convertirse en un modelo lineal equivalente. Esto se logra fijando en uno al denominador de la función objetivo del modelo no lineal e incorporando esto como una nueva restricción del modelo, con lo cual el numerador medirá directamente la eficiencia.

Dado lo anterior, la estructura del modelo de programación lineal es:

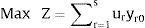(3)

Sujeto a: ∑_r=1^su_ry_rj - ∑_i=1^mv_ix_ij ≤ 0 y ∑_i=1^mv_ix_i0 = 1 j=1,2,..n ur,vi ≥ 0

La solución de estos n modelos lineales provee el conjunto de valores de u_r y v_i que representan los pesos relativos de los inputs y outputs involucrados.

La solución a este problema de programación lineal (primal) se puede encontrar planteando su modelo dual (en la metodología DEA es llamado modelo en forma envolvente).

4.2 Modelo básico de Banker, Charnes y Cooper

Banker, Charnes y Cooper realizan una extensión del modelo DEA-CCR y lo llaman DEA-BCC. El planteamiento de este modelo básico es igual al modelo DEA-CCR; la diferencia se encuentra en que este modelo introduce el supuesto de rendimientos variables a escala.

El modelo DEA-BCC output orientado busca la maximización de los outputs, dado el nivel de inputs, teniendo en cuenta el supuesto de rendimientos variables a escala, como se observa a continuación:

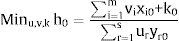(4)

Sujeto a: ∑_i=1^mv_ix_i0 + k₀ / ∑_r=1^su_ry_r0 ≥ 1 j = 1,2,...n ur,vi ≥ 0

El modelo anterior está planteado de manera fraccional y también se puede expresar como un modelo lineal, como en el caso anterior en su forma envolvente, como se observa en la siguiente ecuación:

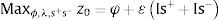(5)

Sujeto a λY = φy₀+s⁺, ,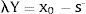

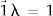
Donde φ denota la puntuación de eficiencia; λ es el vector (nx1) de pesos o intensidades; Y es la matriz de outputs de orden sxn; y₀ representa el vector output de la unidad que está siendo evaluada; X es una matriz de inputs de orden mxn; x₀ representa el vector inputs de la unidad que está siendo evaluada; Is⁺ es el vector de holguras output, e Is⁻ es el vector de holguras input.

La resolución de este modelo dará una solución φ*, s*⁺, s*⁻ de tal forma que φ* ≥ 1. Por lo tanto, cuanto mayor sea φ* más ineficiente será la unidad evaluada. Por esto, una unidad será calificada como técnicamente eficiente si y solo si φ* = 1 y todas las holguras son nulas, es decir, s*⁺ = 0 y s*^- = 0 (eficiencia en el sentido de Pareto Koopmans). En caso contrario, la unidad será ineficiente.

En general, la eficiencia técnica output de la unidad evaluada será igual a 1/φ*. En este sentido, la eficiencia en el sentido de Pareto Koopmans indica que una unidad es eficiente si y solo si φ* = 1 y todas las holguras son cero. Esta situación se puede explicar a través de un gráfico; de esta forma, en la figura 1 se consideran dos inputs y un output, donde las unidades A, B, C, D son eficientes técnicamente según la condición de eficiencia de Farrell, que indica que la puntuación de eficiencia tiene que ser φ* = 1 (estar sobre la frontera). Por otra parte, la unidad E es ineficiente. Sin embargo, solo las unidades B y C son eficientes técnicamente según la condición de Pareto Koopmans, ya que tanto la unidad A como la D presentan holguras input, la primera en el input x₂ y la segunda en el input x₁, que indicarán en cuanto las unidades A y D deberían reducir el consumo de dichos inputs, permaneciendo aun así en la frontera. Finalmente, ninguna unidad presenta holgura output (Coll y Blasco, 2006).

Figura 1 Ejemplo de frontera eficiente.

Centrando la atención en las unidades ineficientes, si se comparan sus valores objetivos y observados es posible determinar la mejora (reducción input y/o incremento output) que debería experimentar cada una de ellas para convertirse en eficiente, así como también se puede distinguir qué parte de dicha mejora se debe a un movimiento radial (derivado de la puntuación de eficiencia obtenida) o un movimiento holgura (derivado del desplazamiento a través de la propia frontera). De esta forma, la mejora potencial es la suma del movimiento radial más el movimiento holgura.

Siguiendo con este razonamiento, ''para toda unidad ineficiente puede obtenerse un punto de proyección sobre la frontera eficiente que represente a una unidad (real o virtual) eficiente'' (Coll y Blasco, 2006, p. 48). Por ejemplo, en la figura 1 se desprende que para E el punto de proyección sobre la frontera eficiente que determinará la dirección de mejora será E’. Por lo tanto, de la comparación entre los valores observados para la unidad ineficiente y los valores objetivos fijados para E’ se establecerá ''la cuantía en términos absolutos o relativos de la reducción input y/o incremento output que E debería tratar de promover para convertirse en eficiente'' (Coll y Blasco, 2006, p. 48).

En el presente caso de estudio, el modelo DEA empleado fue el BCC output orientado. La selección de este modelo se basó en el objetivo de maximizar el output y la opción de rendimientos variables, en donde la adición o disminución de un profesor y/o un auxiliar no se refleja proporcionalmente en el aumento del output (Bandeiras, 2000).

Para determinar la cantidad de inputs y outputs se utilizó la siguiente ecuación (Bandeiras, 2000).

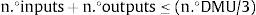(6)

De esta forma, los inputs y outputs considerados en un primer momento fueron:

• Inputs: cantidad de profesores, auxiliares de docencia, personal técnico-administrativo e infraestructura (biblioteca y laboratorios de computación).
• Outputs: cantidad de estudiantes inscritos, aprobados, ausentes y cantidad de horas aula por semana.

De los inputs y outputs mencionados solo fue posible conseguir información para cada una de las 28 asignaturas, correspondiente a: cantidad de profesores (x1: input 1), cantidad de auxiliares de docencia (x2: input 2), cantidad de estudiantes inscritos, aprobados y ausentes (a partir de esta última información se construyó la variable cantidad de estudiantes atendidos y1: output). Respecto a los restantes, no se dispuso de datos completos para todas las asignaturas. Referente al software que se utilizó para correr el modelo propuesto, este fue DEA-solver.

5. Resultados

Dado lo anterior, las materias se agruparon en dos clúster, uno de ''asignaturas curriculares (obligatorias)'' y el otro de ''asignaturas optativas'', a fin de asegurar la suposición de homogeneidad de las DMU a comparar en cuanto a su eficiencia (Dyson et al., 2001).

De esta forma, para el clúster ''asignaturas optativas'' los resultados obtenidos se muestran en la tabla 1.

Tabla 1 Ranking de materias optativas

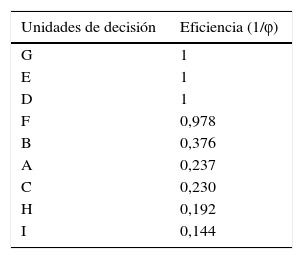
Fuente: elaboración propia.

A partir de lo anterior, las materias G, E y D presentan eficiencia técnica pura output y por lo tanto son las que determinan la frontera eficiente, bajo el supuesto de rendimientos variables. El resto de las materias son calificadas como ineficientes, ya que podrían aumentar el output y seguir utilizando la misma cantidad de recursos; por ejemplo, la materia B tiene una puntuación de eficiencia técnica (output) aproximadamente del 37%.

Complementando lo anterior, en la tabla 2 se presentan los valores observados, los valores objetivos (los valores proyectados sobre la frontera) y la mejora potencial (en porcentaje) que debería experimentar cada unidad de decisión ineficiente en sus inputs y outputs para situarse en la frontera y ser eficiente en el sentido de Pareto Koopmans.

Tabla 2 Proyección de mejora para las materias optativas ineficientes

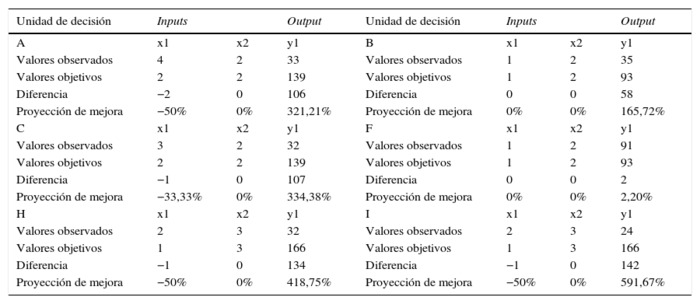
Fuente: elaboración propia.

De la tabla 2 se desprende que, para llegar a ser eficiente, B debería aumentar el output en un 165,72%. Traducido esto a la variable output, significa que, con la cantidad de docentes disponibles, la cantidad de estudiantes que debería estar atendiendo esta asignatura sería de 93, cuando realmente atiende a 35. Además, esta asignatura no presenta holguras en el input.

Al evaluar las materias ineficientes se observó que algunas no solo tienen que aumentar la cantidad de estudiantes atendidos, sino que también deben reducir la cantidad de docentes profesores, mientras que ninguna debería reducir la cantidad de docentes auxiliares.

En el sector educación esto podría ser interpretado de la siguiente manera: las asignaturas optativas ineficientes podrían atender a una mayor cantidad de estudiantes con sus recursos actuales e incluso algunas deberían reducir la cantidad de profesores. De esta forma, el hecho de que ahora no sean eficientes y quieran serlo en el futuro implicará hacer un esfuerzo para evitar la deserción en estas cátedras y aumentar la promoción y divulgación de las mismas para aumentar la cantidad de estudiantes atendidos.

Por otra parte, para el clúster de asignaturas obligatorias, los resultados obtenidos se muestran en la tabla 3.

Tabla 3 Ranking de materias obligatorias

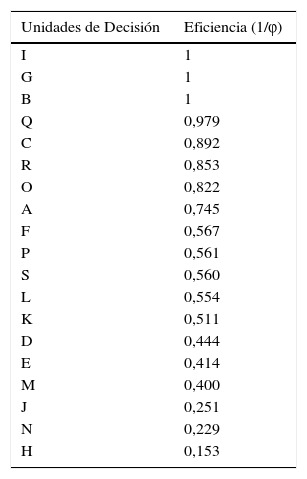
Fuente: elaboración propia.

En el caso de las materias obligatorias, solo I, G, B resultaron ser eficientes, el resto se consideran ineficientes (tabla 3). Por otra parte, la tabla 4 presenta los porcentajes de mejora que deberían realizar cada una de las materias ineficientes para llegar a serlo.

Tabla 4 Proyección de mejora para materias obligatorias ineficientes

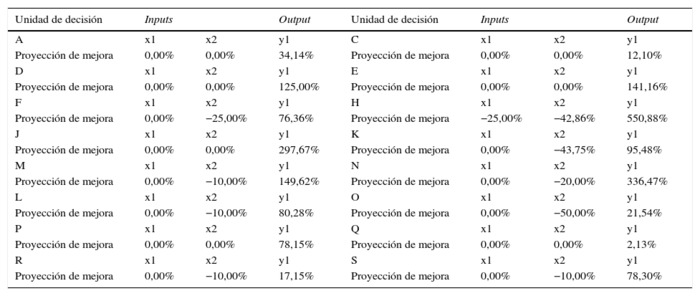
Fuente: elaboración propia.

Por ejemplo, la asignatura C debería incrementar la cantidad de estudiantes atendidos en un 12,10%, mientras que la asignatura F debería no solo aumentar la cantidad de estudiantes atendidos sino también reducir la cantidad de docentes auxiliares. Esto último se repite para las materias K, M, N, L, O, R, S. Solo la materia H debería aumentar su output y al mismo tiempo reducir sus dos inputs, es decir, docentes profesores y auxiliares de la materia.

Estos resultados de mejora difieren de los mostrados para las materias optativas, donde en ningún caso había que reducir la cantidad de auxiliares.

En la tabla 4 se observa que muchas de las asignaturas deberían aumentar en un gran porcentaje la cantidad de estudiantes atendidos. Como en este caso estas materias no son elegidas libremente por los estudiantes sino que son obligatorias, estos valores podrían estar reflejando la deserción o la caída de la matrícula de estudiantes en esta carrera, o bien podrían servir para las personas que toman decisiones en relación con esta carrera para ver hasta qué cantidad de estudiantes podría llegar a atender una cátedra con la cantidad de docentes de que dispone.

6. Consideraciones finales

El método que se está proponiendo en este caso de estudio no pretende ser considerado como la única herramienta a ser tenida en cuenta para la evaluación del desempeño y mejora de la eficiencia de las unidades consideradas. Sin embargo, la dificultad para establecer una función de producción a nivel educativo que combine inputs y outputs en una agregación con valor económico hace necesaria la utilización de métodos no paramétricos para evaluar la eficiencia en este sector. Entre este tipo de métodos cuantitativos se encuentra el DEA. Los modelos DEA básicos propuestos no son los únicos, sino que existen modelos alternativos que no han sido considerados en esta etapa de investigación del caso de estudio.

El modelo DEA empleado fue el BCC output orientado. La selección del modelo se basó en el objetivo de maximizar el output y la opción de rendimientos variables, en que la adición o disminución de un profesor y/o un auxiliar no se refleja proporcionalmente en el aumento del output.

Los resultados obtenidos permitieron identificar cursos optativos ineficientes que, para llegar a ser eficientes, deberían aumentar la cantidad de estudiantes atendidos y reducir la cantidad de profesores, así como cursos obligatorios donde, además de aumentar la cantidad de estudiantes atendidos y reducir la cantidad de profesores, se debería reducir la cantidad de docentes auxiliares.

Los resultados obtenidos para el caso de las asignaturas optativas permiten inferir que los cursos ineficientes podrían atender a una mayor cantidad de estudiantes con sus recursos actuales e incluso algunas deberían reducir la cantidad de profesores. El hecho de que ahora no sean eficientes y quieran serlo en el futuro implicará hacer un esfuerzo para evitar la deserción en estas cátedras y aumentar la promoción y divulgación de las mismas, para así incrementar la cantidad de estudiantes atendidos.

En el caso de los cursos obligatorios, la ineficiencia presente en algunos cursos no solo estaría marcando la forma ineficiente en que se utilizan los recursos económicos del sector público, sino que estos valores podrían estar reflejando la deserción o la caída de la matrícula de estudiantes en esta carrera. Estas conclusiones obtenidas podrían servir para las personas que toman decisiones con relación a esta carrera para ver hasta qué cantidad de estudiantes podría llegar a atender una cátedra con la cantidad de docentes que dispone o cuál sería el nivel de gasto en exceso que le estaría generando esta ineficiencia.

Dentro de las limitaciones del estudio se puede considerar la dificultad en la obtención de la información para determinar los inputs y los outputs para la construcción del modelo, ya que solo se contó con la información disponible en la Memoria Anual del Departamento.

7. Preguntas de discusión

• ¿Qué otros modelos alternativos podrían considerarse para este caso de estudio?
• ¿Qué inputs y outputs hubiera considerado si el estudio de caso se realizara en una carrera de su universidad?
• ¿Para qué otros casos podría aplicarse esta metodología?
• ¿Cree que los resultados podrían estar reflejando la deserción o la caída de la matrícula de alumnos en esta carrera?

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.

Bibliografía

Ahn, T., Charnes, A. y Cooper, W. (1988). Some statistical and DEA evaluations of relative efficiencies of public and private institutions of higher learning. Socio- Economic Planning Sciences, 22(6), 259-269.

Alberca, P. y Parte, L. (2013). Evaluación de la eficiencia y la productividad en el sector hotelero español: un análisis regional. Investigaciones Europeas de Dirección y Economía de la Empresa, 19(2), 102-111.

Alberto, C. y Curchod, M. (2011). Ranking DEA. Una valoración en el sector público nacional. Anales XXIV ENDIO-XXII EPIO, 155-168.

Bandeiras, D. (2000). Análise da eficiência relativa de departamentos académicos o caso da UFRGS. Tese Maestria. Universidade Federal do Rio Grande do Sul, Escola de Administração [consultado 28 Nov 2010]. Disponible em: Disponible em: http://www.lume.ufrgs.br/handle/10183/1845

Charnes, A., Cooper, W. y Rhodes, E. (1981). Evaluating program and managerial efficiency: An application of data envelopment analysis to program follow through. Management Science, 27(6), 668-697.

Coll, V. y Blasco, O. (2006). Evaluación de la eficiencia mediante el análisis envolvente de datos [consultado 30 Mar 2015]. Disponible en: Disponible en: http://www.eumed.net/libros/2006c/197/

Coria, M.M. (2011). Eficiencia técnica de las universidades argentinas de gestión estatal. Ensayos de Política Económica, 5 [consultado 27 Feb 2017]. Disponible en: Disponible en: http://bibliotecadigital.uca.edu.ar/repositorio/revistas/eficiencia-tecnicauniversidades-argentinas.pdf

Dyson, R., Allen, R., Camanho, A. S., Podinovski, V., Sarrico, C. y Shale, E. A. (2001). Pitfalls and protocols in DEA. European Journal of Operational Research, 132, 245-259.

Farrell, M. (1957). The measurement of productive efficiency. Journal of the Royal Statistical Society, 3(120), 253-290.

Gómez, J. M. (2016). Análisis de la variación de la eficiencia en la producción de biocombustibles en América Latina. Estudios Gerenciales, 32, 120-126.

Kao, C. y Hung, H. (2008). Efficiency analysis of university departments: An empirical study. Omega, 36, 653-664.

Kuah, C. T. y Wong, H. Y. (2011). Efficiency assessment of universities through data envelopment analysis. Procedia Computer Science, 3, 449-506.

Legaz, S. G. (1998). El análisis envolvente de datos como sistema de evaluación de la eficiencia técnica de las organizaciones del sector público: Aplicación en los equipos de atención primaria. Revista Española de Financiación y Contabilidad, 27(97), 979-1004.

Maçada, A. (2001). Impacto dos investimentos em tecnologia da informação nas variáveis estratégicas e na eficiência dos bancos brasileiros [ tese doutorado em Administracion. Universidade Federal do Rio Grande do Sul]. Escola de Administração [ consultado 28 Nov 2010]. Disponible en: Disponible en: http://www.lume.ufrgs.br/handle/10183/1845

Marinho, A., Resende, M. y Façanha, L. (1997). Brazilian federal universities: Relative efficiency evaluation and data envelopment analysis. Revista Brasileira de Economia, 51(4), 489-508.

Rhodes, E. (1978). Data Envelopment Analysis and Approaches for Measuring the Efficiency of Decision Making Units with an Application to Program Follow-Through in U.S. Education [Ph.D. dissertation]. School of Urban and Public Affairs, Carnegie- Mellon University.

Rhodes, E. L. y Southwick, L. (1993). Variations in public and private university efficiency. Public Policy Applications of Management Science, 7, 145-170.

Sarrico, C., Hogan, S., Dyson, R. y Athanassopoulos, A. (1997). Data envelopment analysis and university selection. Journal of the Operational Research Society, 48(12), 1163-1177.

Sarrico, C. y Dyson, R. (2000). Using DEA for planning in UK universities - an institutional perspective. Journal of the Operational Research Society, 51, 589-800.

Ventura Blanco, J. (1999). Perspectivas Económicas de la Educación. Barcelona: Universidad de Barcelona.