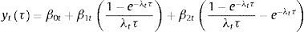 (1)
(1)Artículo
DOI: 10.1016/j.estger.2017.02.003
Medición del valor en riesgo de portafolios de renta fija usando modelos multifactoriales dinámicos de tasas de interés
Measuring the value at risk of fixed-income portfolios using interest rate multi-factor dynamic models
Medição do valor em risco de carteiras de renda fixa usando modelos multifatoriais dinâmicos de taxas de juro
Sara Isabel Álvarez-Francoa, Diego Alexander Restrepo-Tobónb,* , Mateo Velásquez-Giraldo c
a Egresada Maestría en Finanzas, Escuela de Economía y Finanzas, Universidad EAFIT, Medellín, Colombia
b Profesor Asociado, Escuela de Economía y Finanzas, Universidad EAFIT, Medellín, Colombia
c Asistente de investigación, Escuela de Economía y Finanzas, Universidad EAFIT, Medellín, Colombia
* Autor para correspondencia. Carrera 49 No. 7 Sur-50, Medellín, Colombia. Correo electrónico: drestr16@eafit.edu.co (D.A. Restrepo-Tobón).
Historia del artículo:
Recibido el 16 de junio de 2016
Aceptado el 17 de febrero de 2017
On-line el 3 de abril de 2017
Resumen
En este trabajo se evalúa el desempeño de tres modelos dinámicos de la estructura a plazos de tasas de interés para estimar el valor en riesgo (VaR, por su traducción de Value at Risk) de portafolios de renta fija. De esta forma, se encuentra que el modelo de Diebold, Rudebusch y Aruoba se desempeña adecuadamente respecto a las pruebas de backtesting del VaR, mientras que el modelo de Diebold y Li y un modelo afín de no arbitraje exhiben un pobre desempeño. Los tres modelos asumen que la matriz de varianzas y covarianzas de los factores latentes a cada modelo es constante, lo cual limita su utilidad en el cálculo del VaR. Por lo tanto, modelos que relajen este supuesto deberían ofrecer un mejor desempeño y ser más adecuados para la gestión del riesgo de portafolios de renta fija.
Palabras clave: Tasas de interés; Modelos dinámicos; Valor en riesgo; Portafolios de renta fija.
Códigos JEL: G1. E4. C5.
Abstract
In this article we assess the performance of three interest rate dynamic term structure models in order to estimate the Value at Risk (VaR) of fixed-income portfolios. We find that that the model proposed by Diebold, Rudebusch and Aruoba performs appropriately in VaR backtesting statistical tests, while the model from Diebold and Li and a no-arbitrage akin term structure model display serious problems. The three models assume that the variance-covariance matrix for their underlying factors is constant, which limits their usefulness in estimating the VaR. Therefore, those models that relax this assumption should perform better and be more adequate for risk-management of fixed-income portfolios.
Keywords: Interest rates; Dynamic models; Value at risk; Fixed income portfolios.
JEL classification: G1. E4. C5.
Resumo
Neste artigo, o desempenho de três modelos dinâmicos da estrutura a prazos das taxas de juros para estimar o valor em risco (VaR, por sua tradução de Value at Risk) de carteiras de renda fixa é avaliado. Assim, verificou-se que o modelo de Diebold, Rudebusch e Aruoba funciona adequadamente respeitar no que se refere ao backtesting do VaR; enquanto o modelo de Diebold e Li e um modelo relacionado de não arbitragem apresentam um mau desempenho. Os três modelos assumem que a matriz de variâncias e covariâncias dos fatores latentes em cada modelo é constante, o que limita a sua utilidade no cálculo do Valor em Risco. Portanto, os modelos que relaxam esta hipótese devem proporcionar melhor desempenho e ser mais adequados para a gestão de risco das carteiras de renda fixa.
Palavras-chave Taxas de juros; Modelos dinâmicos; Valor em risco; Carteiras de renda fixa.
Classificações JEL: G1. E4. C5.
1. Introducción
El valor en riesgo (VaR) es una medida de riesgo estadística de pérdidas potenciales del valor de un portafolio de activos financieros que podría ocurrir con una probabilidad determinada durante un horizonte de tiempo específico (Jorion, 2006). ''El VaR responde a la pregunta ¿cuánto puedo perder con x% de probabilidad durante un horizonte de tiempo dado?'' (Longerstaey, 1996, p. 6). A pesar de no ser una medida perfecta, por su simplicidad, comparabilidad y fácil interpretación, el VaR se ha convertido en una medida estándar en la industria para medir la exposición al riesgo de mercado y en una herramienta de supervisión importante para la gran mayoría de instituciones financieras (Berkowitz y O’Brien, 2002; Santos, Nogales, Ruiz y van Dijk, 2012; Abad, Benito y López, 2014; Caldeira, Moura y Santos, 2015)1.
Existen diferentes métodos para calcular el VaR de portafolios tanto de renta fija como de renta variable. Abad et al. (2014) presentan una revisión exhaustiva de las diferentes metodologías de cálculo del VaR para portafolios de renta variable. Su trabajo resalta la existencia de una vasta literatura teórica y empírica respecto al cálculo del VaR para esa clase de activos. En contraste, la literatura respecto al cálculo del VaR para portafolios de renta fija es exigua. Caldeira et al. (2015) califican este hecho como un importante vacío en la literatura financiera, dada la importancia de dichos activos en la conformación de portafolios bien diversificados y a que las particularidades de estos instrumentos exigen metodologías diferentes para el cálculo del VaR.
La metodología propuesta en este artículo es similar a la usada por Caldeira et al. (2015). Dicha metodología se fundamenta en la utilización de una clase general de modelos dinámicos multifactoriales de tasas de interés para el cálculo del VaR. Estos modelos han mostrado un desempeño superior para pronosticar la estructura a plazos de tasas de interés (EPTI) (ver, por ejemplo, Diebold y Li, 2006; Diebold, Rudebusch y Aruoba, 2006; De Pooter, 2007; Beltratti y Colla, 2007; Diebold y Rudebusch, 2011; Rezende y Ferreira, 2011; Diebold y Rudebusch, 2013); por tanto, es de esperarse que sean útiles en el cálculo del VaR. No obstante, como se resalta en la literatura (Kim y Orphanides, 2012; Aït-Sahalia y Kimmel, 2010; Christensen, Diebold y Rudebusch, 2009), estos modelos pueden ser difíciles de estimar. Así, la presente metodología no simplifica el cálculo del VaR respecto a las metodologías tradicionales pero busca hacerlo consistente con la teoría subyacente a los modelos dinámicos de la estructura a plazos de tasas de interés más utilizados en la literatura.
Una importante ventaja de calcular el VaR con base en modelos dinámicos de la EPTI es que dicho método permite que los precios de los activos subyacentes al cálculo del VaR y la distribución empírica de los rendimientos del portafolio sean consistentes con la teoría que soporta estos modelos. En principio, utilizar modelos de la estructura a plazos de tasas de interés para estimar el VaR ofrece la oportunidad de hacer consistente la valoración de los instrumentos con la gestión del riesgo de los mismos, pues ambos se derivan de una misma estructura teórica. Por ejemplo, si se utilizan modelos de no arbitraje como base para calcular el VaR, la distribución empírica subyacente al cálculo del VaR de los precios de los títulos que conforman el portafolio puede hacerse consistente con la condición de no arbitraje (Date y Bustreo, 2015). Otro ejemplo sería que si se utiliza un modelo dinámico donde el precio de mercado por riesgo cambia en el tiempo, los precios de los activos que conforman el portafolio serían consistentes con esta propiedad, propiedad que sería reflejada en el VaR. Adicionalmente, modelos de la estructura a plazos que puedan incorporar el efecto que sobre la misma tienen otras variables macroeconómicas, en principio, podrían ser utilizados para calcular un VaR que responda al efecto de dichas variables.
Teniendo en cuenta la similitud del presente artículo con el trabajo de Caldeira et al. (2015), es importante resaltar las diferencias entre los mismos. Primero, Caldeira et al. (2015) utilizan la aproximación propuesta por Diebold y Li (2006) respecto a los modelos de Nelson y Siegel (1987) y Svensson (1994). En este artículo, además del modelo de Diebold y Li (2006), se utiliza el modelo propuesto por Diebold et al. (2006) y un modelo afín gaussiano de no arbitraje de tasas de interés de tres factores. Este último modelo se adopta basándose en los hallazgos de Velásquez-Giraldo y Restrepo-Tobón (2016), quienes muestran que los modelos afínes de tasas de interés tienen un buen desempeño en pronosticar la EPTI colombiana. Por su parte, Maldonado, Pantoja y Zapata (2015) muestran que el modelo de Diebold y Li (2006) se ajusta adecuadamente a la estructura a plazos de tasas de interés colombiana. Finalmente, Gomez-Restrepo y Restrepo-Tobón (2016) muestran que el modelo de Diebold et al. (2006) con macrofactores tiene un desempeño superior al modelo de Diebold y Li (2006) en pronosticar la EPTI en Colombia.
Segundo, Caldeira et al. (2015) modelan separadamente el rendimiento del portafolio de renta fija y la covarianza entre los factores subyacentes al modelo de Diebold y Li (2006) para luego utilizar ambos componentes para calcular el VaR usando una metodología similar a la del método Delta-Normal (Jorion, 2006). En contraste, en este trabajo se estiman los modelos dinámicos multifactoriales de tasas de interés y luego se utilizan los parámetros estimados para simular, vía simulación Monte Carlo, la futura trayectoria de la EPTI y el valor del portafolio de renta fija para el horizonte de tiempo requerido en la estimación del VaR. De esta forma, se obtiene la distribución del valor del portafolio para el horizonte definido y el VaR se calcula como el cambio en el valor del portafolio correspondiente al percentil apropiado de dicha distribución (1 o 5%).
En este trabajo se utilizan datos para Colombia entre 2003 y 2016. Para estimar diariamente los modelos se utilizan las tasas cero cupón, estimadas por la metodología de Nelson y Siegel (1987), entre los años 2003 y 20132. Para simplificar la estimación del VaR, se considera un portafolio compuesto por un solo título de renta fija correspondiente a un TES del Gobierno Nacional con vencimiento en julio de 2024. Dicha simplificación no implica pérdida de generalidad, dado que la estimación del VaR propuesta del portafolio no depende de forma fundamental del número o de las características de los títulos que lo componen. Sin embargo, considerar un único título reduce significativamente el tiempo de cómputo del VaR.
Los modelos considerados asumen que la dinámica de la estructura a plazos de tasas de interés está determinada por tres factores latentes usualmente asociados al nivel, la pendiente y la curvatura de dicha estructura. Estos tres factores latentes capturan parsimoniosamente la dinámica de la estructura a plazos de tasas de interés y son ampliamente aceptados en la literatura (Litterman y Scheinkman, 1991; Duffee, 2002; Brandt y Chapman, 2003; Pérignon y Smith, 2007). La metodología de estimación del VaR para cada modelo tiene tres etapas. Primero, se estima el modelo de forma secuencial para cada día entre el 2 de enero de 2014 y el 14 de julio de 2016 utilizando los datos disponibles desde el 2 de enero de 2003 hasta el día de valoración. Segundo, para cada uno de esos días se simulan 10.000 trayectorias de los tres factores latentes de la estructura a plazos de tasas de interés y el nivel de la curva de rendimientos para el día siguiente y se valora el portafolio utilizando cada una de las 10.000 trayectorias para cada día desde el 3 de enero de 2014 hasta el 15 de julio de 2016. Tercero, se calcula el VaR del portafolio utilizando el valor del portafolio correspondiente al percentil seleccionado para el cálculo del VaR (1 o 5%). Finalmente, para evaluar el desempeño relativo de los tres modelos respecto al cálculo del VaR, se utiliza la metodología de backtesting utilizando las pruebas de cubrimiento condicional e incondicional del VaR y funciones de pérdida.
A pesar del desempeño superior de los modelos dinámicos de tasas de interés para pronosticar la curva de rendimientos (Diebold y Li, 2006; Diebold et al., 2006; De Pooter, 2007; Beltratti y Colla, 2007; Piazzesi, 2010; Diebold y Rudebusch, 2011; Duffee, 2013; Gürkaynak y Wright, 2012; Diebold y Rudebusch, 2013), los resultados empíricos del presente trabajo indican que ninguno de los tres modelos considerados presenta un desempeño superior uniforme en la estimación del VaR de acuerdo a las pruebas de cubrimiento condicional e incondicional o a las funciones de pérdidas. Adicionalmente, se encuentra que el modelo afín de no arbitraje presenta el mejor desempeño relativo respecto a la estimación del VaR basado en funciones de pérdida y un desempeño inferior al modelo de Diebold et al. (2006) respecto a las pruebas de cubrimiento condicional e incondicional. Estas pruebas indican que el modelo de Diebold et al. (2006) cumple con todas las propiedades deseables para el cálculo del VaR. Por su parte, el modelo de Diebold y Li (2006) sobreestima uniformemente el VaR para todos los días considerados.
Una posible razón del pobre desempeño de los modelos dinámicos en la estimación del VaR, consistente con la evidencia empírica y soportando su utilidad en el pronóstico de las tasas de interés, es que dichos modelos capturan adecuadamente solo el primer momento de la distribución de las tasas de interés a diferentes plazos. Los momentos de orden superior no son adecuadamente capturados, y son estos los que determinan su utilidad en la estimación del VaR de un portafolio de renta fija. La principal conclusión del estudio es que, entre los modelos considerados, el modelo de Diebold et al. (2006) se desempeña adecuadamente respecto a las pruebas del backtesting del VaR y debe ser preferido en aplicaciones empíricas. No obstante, antes de utilizar estos modelos en la estimación del riesgo de portafolios de renta fija, se debe modelar conjuntamente tanto el nivel de las tasas de interés como la evolución de su matriz de varianzas y covarianzas. De esta forma, los trabajos de Pérignon y Smith (2007), Trolle y Schwartz (2009) y Creal y Wu (2015) pueden ser un buen punto de partida.
Lo que resta del presente artículo se organiza de la siguiente forma. La sección 2 expone los antecedentes teóricos de los modelos y metodologías usadas. La sección 3 expone los modelos usados y discute su proceso de estimación, así como el cálculo del VaR y su backtesting. La sección 4 presenta y analiza los resultados empíricos de la investigación. Finalmente, en la sección 5 se presentan las conclusiones de la investigación.
2. Marco teórico
En esta sección se presenta la literatura relacionada tanto con la estimación de la EPTI como de la utilización de la misma en la estimación del VaR de portafolios de renta fija.
2.1 Modelos dinámicos de la estructura a plazos de tasas de interés
Los modelos dinámicos para estimar la EPTI son ampliamente estudiados en la literatura. Algunos ejemplos de revisiones recientes al respecto incluyen Piazzesi (2010), Duffee (2013), Gürkaynak y Wright (2012) y Diebold y Rudebusch (2013). Dentro del estudio de este tipo de modelos, podría argumentarse que la contribución más importante en la estimación de la EPTI fue hecha por Nelson y Siegel (1987). El modelo de Nelson y Siegel (NS, en adelante) contempla tres factores que pueden ser asociados (en el límite) directamente al nivel, la pendiente y la curvatura de la EPTI. Dada su simplicidad, flexibilidad y fácil interpretación, el modelo de NS es el más usado por los analistas financieros y los bancos centrales para la estimación de la EPTI.
El modelo de NS es un modelo estático y sirve para ajustar la EPTI solo para un instante de tiempo dado. Partiendo del modelo de NS, Diebold y Li (2006) y Diebold et al. (2006) proponen versiones dinámicas para estimar la EPTI. Diebold y Li (2006) tienen en cuenta que los parámetros del modelo de NS deben cambiar periodo a periodo y proponen estimarlos usando un vector autorregresivo (VAR) usando datos longitudinales para un periodo de tiempo específico. Diebold et al. (2006) parten del enfoque propuesto por Diebold y Li (2006) y proponen una representación de estado-espacio del modelo para la estimación de los factores latentes de la curva de rendimiento. Usando la metodología de filtro de Kalman, los autores calculan la predicción óptima de rendimiento y el correspondiente error de estimación. Una importante crítica de los modelos dinámicos basados en la especificación de NS es que dichos modelos no cumplen con la condición de no arbitraje. Recientemente, Christensen et al. (2009) generalizaron el modelo de NS imponiendo la condición de no arbitraje y demuestran sus propiedades.
Otra clase de modelos dinámicos de las tasas de interés establece una relación teórica entre las tasas de corto y largo plazo asumiendo que la tasa de corto plazo sigue un proceso estocástico. Los principales estudios de esta clase de modelos son los desarrollados por Vasicek (1977), Cox, Ingersoll Jr y Ross (1985), los cuales son generalizados en Duffie y Kan (1996), quienes muestran que la mayoría de dichos modelos pueden ser categorizados como modelos afín (lineales) de tasas de interés (modelos ATSM, por sus siglas en inglés Affine Term Structure Models), en los cuales las tasas de interés para cada vencimiento pueden ser representadas como una función lineal de factores no observables (variables latentes). Desde su trabajo, los ATSM han recibido una gran atención en la literatura.
Una de las grandes ventajas de los ATSM es que la estructura a plazos construida a partir de los mismos es consistente con la condición de no arbitraje. Sin embargo, como muestra Duffee (2002), dichos modelos no se desempeñan adecuadamente en la mayoría de las aplicaciones empíricas, especialmente respecto al pronóstico por fuera de muestra de la EPTI. Además, la estimación de estos modelos es difícil y sujeta a problemas de identificación de sus principales parámetros (ver, por ejemplo, Kim y Orphanides, 2012; Aït-Sahalia y Kimmel, 2010; Christensen et al., 2009). Sin embargo, aunque la estimación de dichos modelos es todavía numéricamente difícil, desarrollos recientes han demostrado que su capacidad predictiva fuera de muestra ha mejorado sustancialmente (Aït-Sahalia y Kimmel, 2010).
Para el caso colombiano se han presentado diferentes metodologías para la estimación de la EPTI. En uno de los primeros estudios en el ámbito nacional, Arango, Melo y Vásquez (2001) emplean el modelo de NS con el fin de obtener un primer acercamiento de la estructura de la curva en Colombia. Posteriormente, Castro y Melo (2010) analizan la relación existente entre las variables macroeconómicas y la curva de rendimientos. En este estudio, los autores utilizan como modelo referente el presentado por Diebold et al. (2006), estimando los parámetros a través de la aplicación de VaR. En otro estudio, Maldonado et al. (2015) estiman la curva de rendimientos aplicando una reparametrización al modelo de NS con los factores de nivel, pendiente y curvatura; en este trabajo los autores ajustan la tasa de interés mediante filtros de Kalman. Un trabajo más reciente es el presentado por Velásquez-Giraldo y Restrepo-Tobón (2016), quienes, basándose en Aït-Sahalia (2008) y Aït-Sahalia y Kimmel (2010), estiman la EPTI para el mercado colombiano usando ATSM, a partir de lo cual encontraron que los modelos ATSM se desempeñan de forma superior respecto a los otros modelos existentes en el pronóstico de la EPTI.
2.2 Calculo del VaR de portafolios de renta fija
En la presente subsección se discuten los antecedentes del cálculo del VaR para portafolios de renta fija. Caldeira et al. (2015) argumentan que la literatura respecto al cálculo del VaR de portafolios de renta fija es exigua y califican este hecho como un importante vacío en la literatura financiera (ver también Martellini y Meyfredi, 2007). Dada la importancia de los instrumentos de renta fija en la construcción de portafolios bien diversificados, es sorprendente que no haya surgido una literatura igualmente importante dedicada al cálculo del VaR de portafolios de renta variable. Como se mencionó anteriormente, entre las pocas excepciones se encuentran Ferreira (2005), Ferreira y Lopez (2005), Vlaar (2000), Abad y Benito (2007), Martellini y Meyfredi (2007), Su y Knowles (2010), Date y Bustreo (2015) y Caldeira et al. (2015). En esta subsección se revisan cada uno de estos trabajos y se relacionan con la contribución del presente artículo.
En contraste con los rendimientos de las acciones, los rendimientos históricos de los bonos no pueden ser utilizados directamente para el cálculo del VaR de un portafolio de renta fija (Sousa, Esquivel, Gaspar y Real, 2012). La razón es que los plazos (madureces) de las tasas de interés implícitas en los precios históricos de los bonos no corresponden con los plazos que se requieren para el cálculo del VaR. Debido a lo anterior, los métodos tradicionales para el cálculo del VaR de portafolios de renta fija difieren de los métodos utilizados para calcular el VaR de portafolios de renta variable. De estos métodos, los más simples y tradicionales son: 1) duración; 2) mapeo de flujos de caja, y 3) análisis de componentes principales. Una buena presentación de estos modelos se encuentra en Jorion (2006).
A pesar de su simplicidad, ninguno de estos métodos (duración, mapeo de flujos de caja, componentes principales) es completamente satisfactorio en la estimación del VaR de portafolios de renta fija (Jorion, 2006). En primer lugar, el método de la duración solo tiene en cuenta movimientos paralelos de la curva de rendimientos. Por su parte, el método de mapeo de flujos de caja utiliza solo parcialmente la información contenida en la EPTI. Finalmente, el método de componentes principales hace un uso más eficiente de la información contenida en la EPTI pero no cuenta con un soporte teórico adecuado para ser utilizado individualmente en la estimación del VaR de portafolios de renta fija. Además, un componente esencial de estos métodos es la modelación de los rendimientos del portafolio, de su varianza histórica, o de la matriz de varianzas y covarianzas en los métodos de mapeo de flujos de caja y de componentes principales. Sin embargo, la literatura existente respecto a la modelación de las tasas de interés y de su volatilidad con propósitos de medir el VaR de portafolios de renta fija es poca.
Debido a las limitaciones discutidas, se han buscado metodologías alternativas. Por ejemplo, Vlaar (2000) usa modelos univariables de series de tiempo para investigar las propiedades estadísticas del VaR de 25 portafolios de renta fija para el mercado alemán. Vlaar compara tres métodos: 1) simulación histórica (SH); 2) varianza-covarianza (VC), y 3) simulación Monte Carlo (SMC). El método de SH consiste en calcular la distribución empírica de los rendimientos del portafolio para un horizonte de tiempo determinado (uno, dos, cinco años). Este método asume que la distribución de rendimientos histórica del portafolio permanecerá estable y es representativa de la evolución del mismo durante los próximos 10 días. En su estudio, Vlaar (2000) usa 250, 550, 750, 1.250 y 2.550 periodos de 10 días de rendimientos y calcula sus correspondientes distribuciones empíricas. Con ello, el VaR del portafolio es calculado como el percentil 1% de la correspondiente distribución empírica. Sus resultados indican que este método subestima el VaR cuando en la simulación histórica se utilizan menos de 750 periodos de 10 días de rendimientos y lo sobreestima cuando se toma 1.250 o más. La razón es que los datos corresponden a periodos de tiempo donde la volatilidad de las tasas de interés se redujo significativamente. De esta forma, Vlaar (2000) concluye que el método de la SH no ofrece una medida precisa del VaR; la principal razón es que el método de SH es sensible a cambios en la dinámica de las tasas de interés que disten del comportamiento típico histórico.
El segundo método usado en Vlaar (2000) es el de SMC. Este método requiere hacer un supuesto sobre la distribución conjunta de los rendimientos de las fuentes de riesgo; en este caso, las tasas de interés. Así, el método requiere un supuesto sobre la media del cambio de las tasas de interés a diferentes plazos, calcular la matriz de varianzas y covarianzas de los cambios entre las tasas de interés a diferentes plazos y asumir una distribución particular. Los parámetros necesarios para dicho cálculo se realizan con información de cinco años anteriores a la fecha para la cual se calcula el VaR. Una característica importante del método es que el cambio esperado en el valor del portafolio se asume igual a cero. Además, se asume que las varianzas de las tasas de interés siguen un proceso Generalized AutoRegressive Conditional Heteroskedasticity (GARCH) y que la distribución normal o la t de Student capturan la relación estadística entre las tasas de interés. Una vez se obtienen los parámetros (media, varianzas y covarianzas) de la distribución, se procede a simular 10.000 realizaciones de los cambios en las tasas de interés para cada día en el que se calcula el VaR y se valoran los portafolios.
Los resultados presentados por Vlaar (2000) indican que el método de SMC subestima el VaR en la mayoría de los casos. Además, los VaR calculados difieren significativamente a lo largo del tiempo, lo cual indica que pequeños cambios en los parámetros estimados llevan a grandes cambios en las simulaciones. También encuentra que los VaR calculados con base en la distribución t de Student fueron inferiores a los calculados con la distribución normal. Dado que la primera tiene colas más pesadas que la distribución normal, este resultado es sorpresivo. Sin embargo, Vlaar (2000) argumenta que la estimación por máxima verosimilitud de la matriz de varianzas y covarianzas para la distribución t de Student da menos ponderación a la ocurrencia de valores extremos. Respecto al método de VC, el promedio de los VaR estimados son de magnitud casi idéntica a los calculados con el método de SMC. No obstante, el método VC tiene un buen desempeño respecto al número de violaciones del VaR, es decir, al número de veces en que la pérdida del portafolio excede al VaR. Por esta razón, Vlaar (2000) recomienda el método de VC sobre los demás.
Otras dos contribuciones importantes respecto a la evaluación empírica del cálculo del VaR para portafolios de renta fija son los trabajos de Ferreira (2005) y Ferreira y Lopez (2005). Ferreira (2005) modela la dinámica de la varianza y la covarianza de las tasas de interés de corto plazo de Alemania y Francia para el periodo que precede la entrada en vigencia del euro, a partir de lo cual encuentra que un modelo bivariado y asimétrico de series de tiempo con efectos de nivel es el que mejor caracteriza la dinámica de la matriz de varianzas y covarianzas entre las tasas de corto plazo en Francia y Alemania. De esta forma, el mejor desempeño para pronosticar dicha matriz lo ofrece un modelo de componentes de errores (VECH, por sus siglas en inglés Vector Error Correction with Heterocedasticity) con efectos de nivel pero sin efectos cruzados entre la volatilidad de la tasa de corto plazo francesa y alemana. Ferreira y Lopez (2005) encuentran que los modelos de ponderación exponencial constante de medias móviles (EWMA, por sus siglas en inglés Exponentially Weighted Moving Average) tienen un desempeño similar pero son significativamente más simples de estimar.
Soportados en los hallazgos de Ferreira (2005), Ferreira y Lopez (2005) modelan el VaR de un portafolio de ponderaciones iguales de posiciones de corto plazo en el mercado de renta fija alemán, francés y japonés, usando varios modelos de series de tiempo para capturar la dinámica de la matriz de varianzas y covarianzas del portafolio. Ferreira y Lopez (2005) encuentran que los modelos con mejor desempeño estadístico en el pronóstico de la matriz de varianzas y covarianzas son aquellos que capturan la volatilidad de acuerdo al nivel de las tasas de interés. Sin embargo, cuando el criterio es el desempeño en el cálculo del VaR, los resultados son altamente sensibles a los supuestos sobre la distribución de las tasas de interés. Al igual que Ferreira (2005), encuentran que modelos simples, como el EWMA, se desempeñan mejor en el cálculo del VaR.
Estos trabajos, sin embargo, no se fundamentan en ninguna teoría que describa la EPTI para la modelación del VaR de portafolios de renta fija. De acuerdo a la revisión de la literatura, el primer trabajo en considerar la utilización de modelos de la EPTI en el cálculo del VaR de portafolios de renta fija es Abad y Benito (2007). Estos autores proponen estimar el VaR de un portafolio de renta fija utilizando SMC. La idea principal en su contribución es utilizar el modelo de NS para valorar los bonos considerados dentro del portafolio. Así, el valor de cualquier bono dentro del portafolio se puede expresar en función de los cuatro parámetros del modelo de NS y, por tanto, el valor total del portafolio depende exclusivamente de las características de los bonos dentro del portafolio y de los cuatro parámetros del modelo de NS. Luego, Abad y Benito (2007) especifican un modelo que describe la evolución de dichos parámetros. Una vez especificado dicho modelo, utilizan SMC para simular la distribución de rendimientos del portafolio ante choques a la evolución de los parámetros del modelo de NS. De esta forma, el cálculo del VaR del portafolio corresponde al percentil x% seleccionado para su cálculo. Adicionalmente, Abad y Benito (2007) seleccionan modelos ARIMA unifactoriales para modelar la dinámica de los parámetros del modelo de NS. Sin embargo, los autores concluyen que los movimientos generados en las tasas de interés al utilizar estos modelos en la SMC son, en su mayoría, implausibles. Por ello, los valores del VaR calculados siguiendo su procedimiento fueron considerados demasiado altos como para ser útiles en la gestión del riesgo de portafolios de renta fija.
El siguiente trabajo existente en la literatura corresponde a Martellini y Meyfredi (2007). Estos autores también utilizan el modelo de NS para extraer los tres factores dinámicos implícitos en la EPTI, tal como lo exponen Diebold y Li (2006). Luego de extraer los factores, los autores utilizan una función de cópulas para modelar la dinámica conjunta de estos. En contraste con Abad y Benito (2007), quienes consideran que los factores evolucionan independientemente, Martellini y Meyfredi (2007) modelan la dinámica conjunta de estos factores utilizando la función de cópulas t de Student. Utilizando SMC, los autores generan 100.000 simulaciones de los parámetros del modelo de NS utilizando la función de cópulas estimada. Seguidamente se generan 100.000 posibles trayectorias para la EPTI y se valora el portafolio de renta fija, obteniendo la distribución empírica simulada del valor del portafolio. Con esta información, el VaR al x% se calcula como el percentil x% de dicha distribución.
El estudio de Martellini y Meyfredi (2007) presenta evidencia empírica para un portafolio de bonos del mercado francés entre el 6 de febrero de 2004 y el 12 de octubre de 2005 para un total de 434 días de negociación. Primero estiman la curva de rendimientos usando la metodología descrita en el párrafo anterior, con la que encuentran que el R2 de los ajustes de las curvas diarias siempre es superior al 99% y los parámetros son estimados con una alta precisión. Utilizando las pruebas de backtesting de Kupiec (1995), Christoffersen (1998) y Christoffersen y Pelletier (2004), los autores reportan que el VaR al 95 y al 99% de confianza obtenidos con la metodología propuesta satisface todas estas pruebas. Adicionalmente, concluyen que dicha metodología es adecuada para el cálculo del VaR de portafolios de renta fija.
Otra variante del modelo de NS para estimar el VaR es presentada en Su y Knowles (2010). Estos autores proponen tomar una aproximación lineal de primer orden a la ecuación del modelo de NS para hacer que las tasas de interés a diferentes plazos sean una función lineal de tres factores: nivel, pendiente y curvatura de la EPTI. Luego modelan el cambio en el valor del portafolio como una función de la duración, el valor del portafolio y el cambio esperado en las tasas de interés, el cual es una función lineal de los cambios en los factores de nivel, pendiente y curvatura. Su y Knowles (2010) muestran que el VaR del portafolio puede calcularse con la aproximación delta-normal, donde la varianza del portafolio es una función de la matriz de varianzas y covarianzas de los tres factores. Sin embargo, los autores no presentan pruebas de backtesting para evaluar el desempeño del VaR.
Por otra parte, Date y Bustreo (2015) proponen una metodología para calcular el VaR de portafolios de renta fija usando un modelo de la tasa de interés de corto plazo de dos factores. El modelo es calibrado a partir del precio de los bonos transados en el mercado y luego los cambios en los precios de los bonos del portafolio son simulados usando el filtro de Kalman. Una de las principales ventajas de esta aproximación es que los precios de los bonos simulados mantienen la propiedad de ser consistentes con la condición de no arbitraje. Esta es una importante propiedad que no comparte ninguno de los métodos utilizados previamente en la literatura. Date y Bustreo (2015) encuentran que el método propuesto presenta un buen desempeño respecto a las pruebas de backtesting de cubrimiento incondicional y condicional.
El trabajo más reciente, y más afín al presente artículo, es el de Caldeira et al. (2015). Estos autores utilizan especificaciones dinámicas del modelo de NS y de Svensson (1994) para estimar el VaR de portafolios de renta fija. La metodología propuesta puede acomodar una gran cantidad de modelos dinámicos de tasas de interés y heteroscedasticidad condicional de las tasas de interés. Adicionalmente, la metodología permite obtener fórmulas cerradas para valorar los bonos pertenecientes a un portafolio de instrumentos de renta fija en función de los factores latentes de los modelos de NS y Svensson. A partir de estas expresiones, es posible calcular, usando SMC, la distribución de rendimientos del portafolio y, consecuentemente, su VaR. La modelación de los factores latentes sigue la metodología propuesta en Diebold y Li (2006). Una vez obtenidos los factores latentes, su volatilidad es calculada utilizando modelos autorregresivos de correlación dinámica. Para calcular el VaR del portafolio, se simulan trayectorias de los factores latentes para estimar el cambio en el valor del portafolio y se utiliza la matriz de varianzas y covarianzas estimada de los factores para calcular el VaR utilizando el método delta-normal. De acuerdo a los resultados del backtesting, Caldeira et al. (2015) concluyen que dicho método se desempeña adecuadamente como para ser utilizado como modelo interno de cálculo del VaR.
Para Colombia, estudios relacionados con la gestión del riesgo en portafolios de renta fija son los presentados por Melo y Granados (2011), quienes bajo diferentes metodologías analizan el desempeño de estimaciones del VaR y el VaR condicional para un conjunto de activos colombianos, incluyendo el precio implícito de títulos de tesoro a 10 años (TES). A su vez, los autores incorporan dentro de su análisis la verificación de los requerimientos exigidos por la regulación actual en el país de estudio, con el fin de determinar si son suficientes para evaluar apropiadamente las estimaciones del VaR. Los resultados encontrados para la estimaciones del VaR indican que para pronósticos con horizonte de un día el desempeño de las medidas de riesgo es apropiado, pero para el cálculo de un VaR multiperiodo ninguna metodología mide adecuadamente el VaR.
3. Metodología
El presente trabajo considera modelos multifactoriales dinámicos para la estimación de la EPTI. A diferencia de los modelos existentes en la literatura, además de utilizar la versión dinámica del modelo de NS propuesta por Diebold y Li (2006), también se emplea el modelo de Diebold et al. (2006) y un modelo de no arbitraje gaussiano afín de tasas de interés. A continuación se exponen los tres modelos utilizados, en donde se usan dos variaciones modelo de Nelson y Siegel (1987) y ATSM para la estimación de la curva de rendimientos para el mercado colombiano.
3.1 Modelos dinámicos de la EPTI
Existe una gran variedad de modelos dinámicos de tasas de interés que pueden clasificarse en tres grandes categorías. La primera categoría incluye modelos teóricamente rigurosos pero con pobre desempeño empírico. La segunda incluye modelos empíricamente exitosos pero con pobre soporte teórico. Y la tercera incluye modelos que tienen algún sustento teórico y que se desempeñan adecuadamente en la práctica (Diebold y Rudebusch, 2013). A esta última categoría pertenece el modelo dinámico de Nelson y Siegel (DNS) derivado de los trabajos de Diebold y Li (2006) (DL, en adelante) y Diebold et al. (2006) (DRA, en adelante) y el modelo de no arbitraje de Nelson y Siegel (AFNS, en adelante) de Christensen, Diebold y Rudebusch (2011). En el presente trabajo se emplean las versiones DL y DRA. Respecto a los modelos de no arbitraje, se emplea un modelo gaussiano afín de no arbitraje con tres factores (ATSM, en adelante), el cual ha sido empleado con éxito en la práctica (Aït-Sahalia y Kimmel, 2010). A continuación se expone brevemente la especificación de cada uno de estos modelos.
Inicialmente, Diebold y Li (2006) proponen una versión dinámica del modelo estático de NS para modelar la EPTI. De esta forma, su especificación viene dada por:
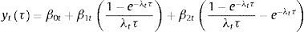 (1)
(1)
donde yt(τ) es un vector de los rendimientos al vencimiento de los títulos con vencimiento en τ, β0t, β1t, β2t son interpretados como factores dinámicos latentes de nivel, pendiente y curvatura, donde, a diferencia del modelo original y estático de NS, estos factores varían en el tiempo. Para hacer que el modelo de la ecuación 1 sea lineal en los parámetros, Diebold y Li (2006) proponen mantener el parámetro λ constante; este parámetro está asociado a la curvatura de la EPTI. En particular, para el mercado de Estados Unidos, Diebold y Li (2006) fijan dicho valor en λ = 0, 0609. Con datos correspondientes al vector yt(τ) y su correspondiente vector de vencimientos τ, para cada periodo t, se estiman los parámetros β0t, β1t, β2t para cada periodo. Por lo tanto, para pronosticar la EPTI para un periodo t + h se utiliza la siguiente especificación:
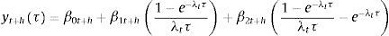 (2)
(2)
donde  para i = 0, 1, 2, y donde los coeficientes
para i = 0, 1, 2, y donde los coeficientes  son estimados utilizando modelos univariados autorregresivos de series de tiempo para cada
son estimados utilizando modelos univariados autorregresivos de series de tiempo para cada  .
.
Bajo el enfoque propuesto por Diebold y Li (2006), Diebold et al. (2006) proponen la siguiente variación al modelo DRA:
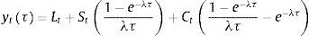 (3)
(3)
donde yt(τ) son los rendimientos de los títulos con vencimiento en τ, y Lt, St, Ct son los factores del modelo (no observables) con variación en el tiempo asociados a nivel, pendiente y curvatura, respectivamente. El valor de λ es igualmente fijado en 0,0609 para el caso de Estados Unidos. El modelo de la ecuación 3 puede especificarse bajo la representación de un sistema de estado-espacio. Partiendo del modelo DL se reformula el proceso que siguen los factores pasando de un AR (1) a un VAR (1), lo cual da lugar a la siguiente especificación:
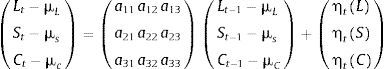 (4)
(4)
donde cada una de las observaciones de las series de datos para nivel, pendiente y curvatura se deflacta con su respectiva media μ. La ecuación de observaciones que relaciona los rendimientos con los factores no observables se escribe como:
 (5)
(5)
donde t = 1,…,T. En notación matricial el modelo se reescribe como el siguiente sistema de estado-espacio con los factores ajustados por su media.
 (6)
(6)
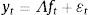 (7)
(7)
donde A es una matriz (3×3) que contiene parámetros no restringidos, μ es un vector de estado (3×1) que contiene parámetros no restringidos y la matriz Λ contiene el parámetro λ y los loadings que acompañan a cada factor. La estimación de los parámetros se realiza a través del filtro de Kalman, lo cual requiere que las perturbaciones de ruido blanco (WN) y de medición sean ortogonales para iniciar el sistema:
 (8)
(8)
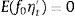 (9)
(9)
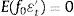 (10)
(10)
donde Q es la matriz de covarianzas de los factores y H es la matriz de covarianza de los rendimientos. El modelo impone la condición de que las perturbaciones del factor de la ecuación de estado ηt están correlacionadas y que por lo tanto la correspondiente matriz de covarianza Q es no diagonal. En el caso de la matriz H, el modelo impone diagonalidad sobre ella, implicando que las desviaciones de los rendimientos para diferentes vencimientos no están correlacionadas.
De otro lado, los ATSM asumen que la tasa de interés de corto plazo es una función afín3 de un vector de estado X(t) de N factores subyacentes, los cuales pueden ser observables (variables macroeconómicas) o latentes (Piazzesi, 2010).
 (11)
(11)
donde y corresponde los rendimientos de la curva cero cupón con vencimiento en τ, δ0 ∈ Rn y el vector δ1 ∈ Rn. De esta forma, se asume que el vector de estado sigue un proceso de difusión afín bajo la medida de riesgo neutral Q:
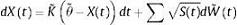 (12)
(12)
donde  es un movimiento browniano independiente N dimensional y S(t) es una matriz diagonal NxN, donde [S(t)]i,i = αi + βiTX(t), con αi, βi ∈ RN.
es un movimiento browniano independiente N dimensional y S(t) es una matriz diagonal NxN, donde [S(t)]i,i = αi + βiTX(t), con αi, βi ∈ RN.
El precio del mercado de riesgo Λ(X) ∈ RN es también especificado en orden de obtener la dinámica física. Siguiendo la literatura, se asume que  donde λ es un vector de constantes (Dai y Singleton, 2000). Por lo tanto, el proceso de estado es también afín bajo la medida P (Duffie y Kan, 1996):
donde λ es un vector de constantes (Dai y Singleton, 2000). Por lo tanto, el proceso de estado es también afín bajo la medida P (Duffie y Kan, 1996):
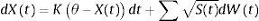 (14)
(14)
Bajo esta estructura, Duffie y Kan (1996) muestran que los rendimientos para cualquier vencimiento τ pueden ser obtenidos como una función afín del vector de estado:
 (15)
(15)
donde los coeficientes A(t) y Bt son la solución del siguiente sistema de ecuaciones diferenciales:
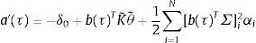 (16)
(16)
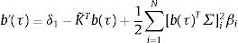 (17)
(17)
Con  . Estas ecuaciones imponen las restricciones de no arbitraje (Duffie y Kan, 1996).
. Estas ecuaciones imponen las restricciones de no arbitraje (Duffie y Kan, 1996).
3.2 Cálculo del VaR de carteras de renta fija
En el presente artículo se propone una metodología para el cálculo del VaR en la cual se simulan escenarios para las tasas de interés futuras de acuerdo con tres modelos de tasas de interés ampliamente utilizados en la literatura. Cada modelo asume que existen tres factores o variables latentes (el nivel, la pendiente y la curvatura) que explican la mayor parte de la dinámica de la EPTI, expresando las tasas de interés (para cualquier plazo) en función de estos factores. De esta manera, y dada la dinámica de estos factores implícitos en cada modelo, se pueden simular trayectorias futuras para los factores y, a partir de su relación con las diferentes tasas de interés para diferentes plazos, obtener tasas de interés simuladas. Esto permite simular un gran número de trayectorias posibles de la futura curva de rendimientos, consistentes con la dinámica implícita de cada modelo. Con estas tasas luego se valoran los títulos dentro del portafolio y se construye la distribución empírica del valor del mismo. Una vez obtenida la distribución empírica simulada del valor del portafolio, se calculan los cambios posibles respecto a su valor actual y se selecciona el percentil de la distribución de cambios del valor del portafolio correspondiente al nivel de confianza con que se está estimando el VaR. La figura 1 ilustra la metodología propuesta para calcular el VaR de portafolios de renta fija a partir de modelos dinámicos de la estructura a plazos de tasas de interés.
Figura 1 Metodología para calcular el VaR del portafolio.
Fuente: elaboración propia.
3.2.1 Estimación de los modelos
A partir de los parámetros calculados por Infovalmer para el mercado de tasas de interés colombiano correspondientes al modelo de Nelson y Siegel (Betas), se calcula la curva de rendimientos diaria entre los años 2003 a 2013. Posteriormente, se calculan los factores de pendiente, nivel y curvatura para cada modelo4. Las estimaciones de los modelos DL y DRA siguen las metodologías utilizadas en Diebold y Li (2006) y Diebold et al. (2006), respectivamente. Por su parte, la estimación de los factores del ATSM se realiza aplicando la técnica de estimación de máxima verosimilitud propuesta por Aït-Sahalia (2008) y Aït-Sahalia y Kimmel (2010) (los detalles de dicha estimación se pueden encontrar en Velásquez-Giraldo y Restrepo-Tobón, 2016). Los vencimientos para los cuales se estiman la curva de rendimientos corresponden a 0,25, 0,5, 1, 2, 4, 5, 7, 8, 9 y 10 años y la estimación se hace para un modelo de tres factores no observables. La tabla 1 presenta las estadísticas descriptivas de las tasas de interés utilizadas para la estimación entre el 3 de enero de 2003 y el 30 de diciembre de 2013. La figura 2 ilustra la curva de rendimientos estimada con la metodología NS para dicho periodo.
Tabla 1 Estadísticas descriptivas de las tasas de interés a diferentes plazos
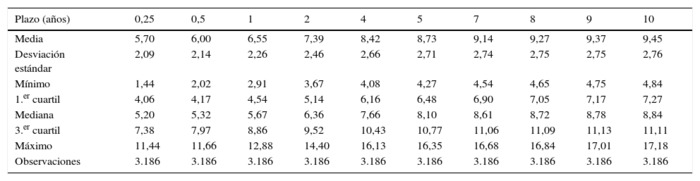
Fuente: elaboración propia con base en los parámetros de NS estimados por Infovalmer.
Figura 2 Tasa de interés para los vencimientos correspondientes a 0,25, 0,5, 1, 2, 4, 5, 7, 8, 9 y 10 años para el periodo de tiempo comprendido entre 2003 y 2013.
Fuente: elaboración propia.
3.2.2 Pronóstico de la EPTI
Con los datos de las tasas de interés entre 2003 y 2013 para los plazos seleccionados, se estiman los factores subyacentes para cada uno de los modelos considerados (DL, DRA y ATSM), comenzando el día 2 de enero de 2014. Con los factores y parámetros estimados para este día se hacen 10.000 pronósticos de la curva de rendimiento para el siguiente día (3 de enero de 2014). Este procedimiento se repite secuencialmente para 615 días adicionales entre el 3 de enero de 2014 y el 14 de julio de 2016, para un total de 616 días. Como resultado se obtienen 10.000 diferentes curvas de rendimiento para cada día y para cada modelo. A continuación se detalla el proceso de pronóstico (simulación) de la curva de rendimientos con cada modelo.
En el caso del modelo DL, se ajusta un modelo autorregresivo AR(1) a cada una de las diferencias diarias de los factores Δβi,t = αi * Δ βi,t−1 + εi,t con i = 0, 1, 2; donde εi,t es una perturbación aleatoria con media cero. Para la simulación de las curvas de rendimiento a un día se adopta una metodología de bootstrapping que consiste en representar la perturbación con una de sus realizaciones anteriores. Así, la ecuación de simulación para cada factor en el modelo de DL es  , donde αi es estimado por OLS y εt corresponde a uno de los residuales de la estimación seleccionado aleatoriamente con reemplazo.
, donde αi es estimado por OLS y εt corresponde a uno de los residuales de la estimación seleccionado aleatoriamente con reemplazo.
Por su parte, el modelo DRA tiene en cuenta la posible relación entre los factores y entre sus perturbaciones. De acuerdo con las ecuaciones 4 y 8, la ecuación de simulación para la obtención de los factores es:
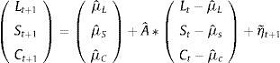 (18)
(18)
donde  es una simulación de una variable aleatoria normal multivariada de media cero y matriz de covarianzas Q. De esta forma, luego de obtener los factores para cada día t, se toma la esperanza de la ecuación (7) para pronosticar las tasas de interés del siguiente periodo.
es una simulación de una variable aleatoria normal multivariada de media cero y matriz de covarianzas Q. De esta forma, luego de obtener los factores para cada día t, se toma la esperanza de la ecuación (7) para pronosticar las tasas de interés del siguiente periodo.
Finalmente, el ATSM es un modelo continuo. Para la simulación a partir de dicho modelo se requiere utilizar un método de discretización. En este caso se aplica el esquema numérico de Euler, obteniendo la siguiente ecuación de simulación:
 (18)
(18)
donde  es una simulación de una variable aleatoria normal estándar y δ = 1/252 dado que se simulan datos diarios. Por su parte, X(t) al ser no observable, debe obtenerse cada día invirtiendo la ecuación (15) para los rendimientos al vencimiento de 0,25, 4 y 10 años.
es una simulación de una variable aleatoria normal estándar y δ = 1/252 dado que se simulan datos diarios. Por su parte, X(t) al ser no observable, debe obtenerse cada día invirtiendo la ecuación (15) para los rendimientos al vencimiento de 0,25, 4 y 10 años.
3.2.3 Cálculo del VaR
Una vez se obtienen las EPTI simuladas para cada modelo y los 616 días, se procede a valorar el portafolio para cada uno de esos días. La valoración se hace con las curvas de rendimientos simuladas para cada uno de los modelos utilizados (DL, DRA, ATSM). De esta forma se obtienen tres distribuciones simuladas del valor del portafolio (una por modelo) para cada día perteneciente al periodo de pronóstico. A partir de la distribución de los valores del portafolio, se puede calcular el cambio en el valor del portafolio con respecto al día anterior, lo cual produce tres distribuciones por día de los cambios en el valor del portafolio. Para calcular el VaR con un nivel de confianza del 95%, se toma el percentil 5 de estas distribuciones como estimación del VaR del portafolio a un día. Para el caso del presente estudio, el portafolio de renta fija está compuesto por el Título del Gobierno Colombiano (TES) con vencimiento en julio de 2024, el cual es uno de los más negociados en el mercado.
3.3 Backtesting
De acuerdo con la literatura, el proceso de backtesting debe ser realizado con más de un método, puesto que los resultados de un solo test pueden no ser suficientes para evaluar el desempeño de un modelo de estimación del VaR (Haas, 2001). En este trabajo se aplican las pruebas de cubrimiento incondicional y cubrimiento condicional del VaR. Estas pruebas, sin embargo, no son apropiadas para comparar el desempeño relativo de los modelos respecto al cálculo del VaR. Para comparar el desempeño de estos modelos se utiliza el método de funciones de pérdida propuesto por Lopez (1999). Estas medidas se describen a continuación.
3.3.1 Pruebas de cubrimiento incondicional
Las pruebas de cubrimiento incondicional se basan en determinar el número de excepciones5 del VaR. Si el número de excepciones es menor que el correspondiente, de acuerdo con el nivel de confianza6 seleccionado, significa que el riesgo del sistema está sobreestimado, y en caso contrario se concluye que el riesgo está siendo subestimado.
Siguiendo a Kupiec (1995), se aplican dos tipos de test que determinan el desempeño de los modelos en cuanto a la estimación del VaR. El primero es el test de proporción de fallos (POF test). Este test compara si el número de excepciones encontradas es consistente con el número de excepciones sugeridas por el nivel de confianza. Bajo la hipótesis nula de que el modelo es correcto, el número de excepciones sigue una distribución binomial. Así, la hipótesis nula se puede escribir como  donde x es el número de excepciones, T es el número de observaciones y p se define como p = (1 − c), donde c es el nivel de confianza bajo el que se realiza el backtesting.
donde x es el número de excepciones, T es el número de observaciones y p se define como p = (1 − c), donde c es el nivel de confianza bajo el que se realiza el backtesting.
De acuerdo con Kupiec (1995), el estadístico LRPOF asociado a la función de verosimilitud se distribuye asintóticamente como una distribución chi-cuadrada con un grado de libertad. El segundo test es la prueba de tiempo hasta el primer fallo (TUFF test) propuesto por Kupiec (1995). Esta prueba tiene como fin medir el periodo de tiempo que se tarda en presentarse la primera excepción y se basa en supuestos similares a los del LRPOF y se distribuye asintóticamente χ2 con un grado de libertad.
3.3.2 Pruebas de cubrimiento condicional
Las pruebas de cubrimiento condicional, al igual que las de cubrimiento incondicional, están basadas en el número de excepciones. Sin embargo, bajo este enfoque se espera que las excepciones se distribuyan uniformemente en el tiempo y que sean independientes; asegurando que la estimación del VaR no se vea significativamente afectada ante cambios de volatilidad y correlaciones. Siguiendo a Christoffersen (1998) y Haas (2001), se aplican dos pruebas que permiten medir el cumplimiento de la propiedad de cubrimiento condicional en la estimación del VaR. La primera es la prueba de intervalos de pronóstico de Christoffersen. Esta prueba, además de contrastar el número de excepciones respecto al ideal teórico, incluye un estadístico para determinar la independencia de las excepciones (determinar si la excepción de un día depende del día anterior). El estadístico para esta prueba está definido por LRcc = LRPOF + LRind, donde LRcc se distribuye χ2 con dos grados de libertad. Otra prueba utilizada en el backtesting es el test mixto de Kupiec (Haas, 2001), dado por LRmix = LRPOF + LRind, donde LRmix se distribuye χ2 con n grados de libertad, siendo n el número de excepciones. De esta forma, el término LRPOF corresponde al sugerido por Kupiec (1995) y el LRind es el estadístico utilizado para poner a prueba la independencia de las excepciones.
3.3.3 Funciones de pérdida
Las funciones de pérdida se basan en determinar la magnitud del exceso reportado entre las excepciones y la pérdida real. Siguiendo la propuesta de Lopez (1998, 1999), se evalúa el desempeño de los modelos de acuerdo con los resultados obtenidos al minimizar las funciones de pérdida. Estas funciones se definen por L = 1 + (xt+1 − VaRt)2 si xt+1 ≤ VaRt(α) e igual a cero en otro caso. En este caso, xt+1 es el retorno realizado del portafolio y el VaRt es el VaR estimado en el momento t (como porcentaje). El estadístico definido para esta prueba se basa en el cálculo de la pérdida promedio de la muestra, la cual es igual a  donde el valor de L para cada modelo es comparado entre estos, de tal forma que el modelo de mejor desempeño es aquel para el cual la función de pérdida es menor.
donde el valor de L para cada modelo es comparado entre estos, de tal forma que el modelo de mejor desempeño es aquel para el cual la función de pérdida es menor.
4. Resultados empíricos
En la tabla 2 se reporta el MSE y RMSE para las tasas de interés estimadas por los tres modelos respecto a las tasas de interés calculadas bajo la metodología de NS. Los tres modelos presentan un alto grado de ajuste para las tasas correspondientes a 0,25, 0,5, 1, 2, 4, 5, 7, 9 y 10 años.
Tabla 2. MSE y RMSE para el periodo de la muestra estimado (2002-2013)

Fuente: elaboración propia.
La figura 3 ilustra el valor del VaR para el periodo comprendido entre el 3 de enero de 2014 y el 15 de julio de 2016. La línea negra muestra al cambio real diario en el valor del portafolio. Por su parte, la línea de tono más tenue ilustra el valor del VaR del portafolio estimado usando el método de duración. En la figura se presentan adicionalmente las estimaciones del VaR obtenidas al usar las metodologías expuestas en la sección 3 para cada uno de los modelos discutidos: ATSM, DRA y DL.
Figura 3. VaR del portafolio (de enero de 2014 a julio de 2016).
Fuente: elaboración propia.
El proceso de backtesting para los 616 diferentes VaR calculados se hace con los niveles de confianza del 90, del 95, del 97,5 y del 99%. Para estos niveles de confianza, el número de veces que se espera que la pérdida real del portafolio sea superior (en valor absoluto) al valor del VaR estimado es 62, 31, 15 y 6, respectivamente. En cuanto al VaR calculado para cada día con el modelo DL no se encuentra ninguna excepción, lo cual es coherente con los resultados ilustrados en la figura 3, donde se observa que bajo este modelo el resultado del VaR sobreestima significativamente la pérdida del portafolio. De otro lado, el número de excepciones que presentan los modelos DRA y ATSM son 4 y 65, respectivamente. Como se ilustra en la figura 3, el VaR calculado para cada día con el modelo ATSM sigue de cerca la verdadera pérdida del portafolio, lo que hace que el número de excepciones sea mayor para este modelo y muy por encima de las excepciones teóricas esperadas (6 a un nivel de confianza del 99% para el backtesting). Finalmente, el número de excepciones para el modelo DRA es significativamente menor (4), número cercano al esperado basado en un nivel de confianza del 99%.
Para determinar si estos valores son estadísticamente diferentes a los esperados para cada nivel de confianza se debe utilizar la prueba POF de Kupiec (1995). La tabla 3 presenta los resultados asociados a esta prueba para cuatro diferentes niveles de confianza. Es importante aclarar que estos niveles de confianza no corresponden a los usados en el calculó el VaR sino al nivel de confianza con el que se pretende realizar la prueba de backtesting. De esta forma, la primera columna indica el modelo, la segunda el nivel de confianza del backtesting, la tercera el valor crítico del test, la cuarta columna el valor del estadístico calculado y la quinta indica si la hipótesis nula de que el número de excepciones es igual a las esperadas se acepte (A) o se rechace (R). Para el modelo DRA, para un nivel de confianza del 99%, se acepta que el número de excepciones observadas (4) está en línea con el número de excepciones esperadas. Para los demás niveles de confianza se rechaza la hipótesis nula. Para el modelo ATSM, solo si se baja a un nivel de confianza inferior al 90% se aceptaría dicha hipótesis. Finalmente, el modelo DL, por sobreestimar sistemáticamente el VaR, no presenta ninguna excepción y, por tanto, no es posible calcular el estadístico de la prueba POF.
Tabla 3. Pruebas de backtesting
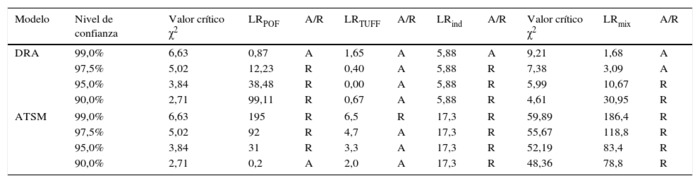
Fuente: elaboración propia.
De acuerdo a estos resultados, los tres modelos se desempeñan pobremente respecto al número de excepciones encontradas versus las esperadas. De un lado, el DRA presenta muy pocas excepciones respecto a las esperadas, mientras que el ATSM presenta muchas. Sin embargo, la prueba POF solo tiene en cuenta el número de excepciones y no cómo esas excepciones se presentan en el tiempo. Como se mencionó anteriormente, la prueba TUFF resuelve este problema. Sin embargo, los resultados de esta prueba deben verse con cuidado, dado que esta tiene un bajo poder y, por tanto, no debe ser un indicador definitivo en cuanto a las conclusiones del desempeño de un modelo en la estimación del VaR.
La siguiente prueba de backtesting considerada es la prueba de independencia de Christoffersen (1998). Para esta prueba se encontró que la hipótesis nula de que las excepciones son independientes en el tiempo se debe rechazar para la mayoría de los niveles de confianza considerados. Por otra parte, aplicando el test mixto de Kupiec, para evaluar la hipótesis nula de que el número de excepciones está en línea con las esperadas y que las mismas ocurren de forma independiente en el tiempo, se encontró que el modelo DRA tiene un desempeño adecuado para niveles de confianza del 97,5 y del 99%.
Respecto a las pruebas basadas en las funciones de pérdida, se encuentra que el modelo que presenta la pérdida más pequeña es el modelo ATSM. El estadístico de Lopez (1999) es igual a 14,19, 3,81, y 1,46, para los modelos DL, DRA y ATSM, respectivamente. Sin embargo, teniendo en cuenta el pobre desempeño del modelo ATSM en las pruebas de backtesting debido a la subvaloración de la pérdida esperada, no es sorprendente que en la prueba de funciones de pérdida este modelo tenga un mejor desempeño.
Tomados en conjunto, los resultados indican que el VaR estimado bajo la metodología propuesta se desempeña pobremente respecto a las principales pruebas de backtesting existentes en la literatura. Este resultado es sorprendente debido a que los modelos dinámicos de tasas de interés han ganado una gran popularidad en los últimos años para modelar la estructura a plazos de tasas de interés. Una de las razones podría ser que, aunque estos modelos son dinámicos, dicha propiedad solo captura la dinámica del nivel de las tasas de interés, pero no la dinámica de sus volatilidades. Los tres modelos investigados asumen que la matriz de varianzas y covarianzas de los factores latentes a cada modelo es constante, lo cual limita su utilidad en el cálculo del VaR. Modelos que relajen este supuesto deberían ofrecer un mejor desempeño y ser más adecuados para la gestión del riesgo de portafolios de renta fija. En futuras investigaciones podría ser fructífero utilizar modelos dinámicos con volatilidad dinámica o estocástica.
5 Conclusiones
Este artículo tiene como objetivo investigar el desempeño relativo de dos clases de modelos dinámicos de estructura a plazo de tasas de interés respecto a la estimación del VaR de un portafolio de renta fija. La principal hipótesis del estudio es que, dado que los modelos dinámicos de tasas de interés han mostrado un buen desempeño empírico en pronosticar la curva de rendimientos, el VaR calculado a partir de estos modelos debería tener un buen desempeño respecto a las pruebas de backtesting más utilizadas en la literatura.
La principal justificación para utilizar estos modelos en el cálculo del VaR es su buen desempeño en pronosticar la curva de rendimientos (Diebold y Li, 2006; Diebold et al., 2006; De Pooter, 2007; Beltratti y Colla, 2007; Piazzesi, 2010; Diebold y Rudebusch, 2011, 2013; Duffee, 2013; Gürkaynak y Wright, 2012). No obstante, los resultados empíricos indican que ninguno de los tres modelos considerados presenta un desempeño superior uniforme en la estimación del VaR de acuerdo a las pruebas de backtesting utilizadas.
Los modelos usados en el presente estudio son el modelo de Diebold y Li (2006), el modelo de Diebold et al. (2006) y un modelo afín gaussiano de no arbitraje. El modelo afín de no arbitraje presenta el mejor desempeño relativo respecto a la estimación del VaR basado en funciones de pérdida, pero es el modelo que lleva a cometer más errores en el cálculo del VaR. En general, este modelo subestima el VaR. Por su parte, el modelo de Diebold et al. (2006) tiene un buen desempeño respecto a las prueba de cubrimiento condicional e incondicional del VaR. Esto indica que dicho modelo podría ser un buen candidato para ser utilizado en el cálculo del VaR. Las pruebas de cubrimiento condicional e incondicional indican que el modelo de Diebold et al. (2006) cumple con todas las propiedades del VaR para niveles de confianza del 97,5 y del 99% en las pruebas de backtesting. Adicionalmente, el valor de la función de pérdida para dicho modelo parece adecuado en comparación con el modelo de Diebold y Li (2006) y el ATSM. Por el contrario, el modelo de Diebold y Li (2006) sobreestima uniformemente el VaR para todos los días considerados.
Una posible razón que explica el pobre desempeño de los modelos dinámicos en la estimación del VaR es que dichos modelos capturan adecuadamente solo el primer momento de la distribución de las tasas de interés a diferentes plazos. Esta hipótesis es consistente con la evidencia empírica soportando su utilidad en el pronóstico de las tasas de interés. No obstante, al parecer los momentos de orden superior de las tasas de interés a diferentes plazos no son adecuadamente capturados y son precisamente estos momentos los que determinan su utilidad en la estimación del VaR. Esto podría deberse a que los modelos dinámicos de tasas de interés asumen que la matriz de varianzas y covarianzas de los factores latentes que explican la dinámica de la estructura a plazos de tasas de interés es constante. Relajar este supuesto parece conducir a mejores resultados. Por ejemplo, Caldeira et al. (2015) modelan dicha matriz asumiendo que las volatilidades de dichos factores cambian en el tiempo y obtienen resultados apropiados en cuanto al cálculo del VaR. No obstante, Caldeira et al. (2015) modelan la volatilidad de dichos factores independientemente del primer momento de la distribución, lo cual es inconsistente con los supuestos realizados en la estimación de los modelos.
De esta forma, la principal conclusión del estudio es que entre los modelos considerados, el modelo de Diebold et al. (2006) se desempeña adecuadamente respecto a las pruebas del backtesting del VaR y debe ser preferido en aplicaciones empíricas. No obstante, antes de utilizar dichos modelos en la estimación del riesgo de portafolios de renta fija, se debe modelar conjuntamente tanto el nivel de las tasas de interés como la evolución de su matriz de varianzas y covarianzas. Debe tenerse en cuenta que la utilidad de dichos modelos para estimar el VaR de portafolios de renta fija debe ser sopesada respecto a los costos asociados a la implementación y estimación de dichos modelos. Con respecto a este punto, los trabajos de Pérignon y Smith (2007), Trolle y Schwartz (2009) y Creal y Wu (2015) pueden ser un buen punto de partida, lo cual se deja para futuras investigaciones.
Conflicto de intereses
Los autores declaran no tener ningún conflicto de intereses.
Notas
1 En Colombia, la Superintendencia Financiera regula y supervisa la exposición al riesgo de tasas de interés de portafolios de renta fija utilizando la medida del VaR. Al respecto, la regulación actual contempla dos alternativas para el cálculo de esta medida: 1) metodología estándar desarrollada por el ente regulador, y 2) modelos internos propuestos por cada entidad financiera.
2 Como muestran Velásquez-Giraldo y Restrepo-Tobón (2016), la estimación de los modelos multifactoriales dinámicos utilizando tasas cero cupón derivadas con la metodología no paramétrica de bootstrapping conlleva resultados similares.
3 Una función F : RN → RMse dice que es afín si F(X) = A + B * X para un vector A y una matriz B.
4 El valor de λ para el modelo DL se fija como el promedio de este parámetro estimado para Colombia por la metodología de NS. Siguiendo a Diebold et al. (2006), en el modelo de DRA este parámetro se hace igual al valor correspondiente al vencimiento que hace que el componente exponencial del factor de curvatura sea máximo.
5 Las excepciones corresponden al número de días (periodo de tiempo) en los cuales las pérdidas reales del portafolio exceden el VaR estimado.
6 El nivel de confianza del backtesting no está relacionado con el nivel de confianza usado para la estimación del VaR.
Bibliografía
Abad, P. y Benito, S. (2007). Value at risk in fixed income portfolios: A comparison between empirical models of the term structure. The Business Review Cambridge, 7(2), 342.
Abad, P., Benito, S. y López, C. (2014). A comprehensive review of Value at Risk methodologies. The Spanish Review of Financial Economics, 12(1), 15–32.
Aït-Sahalia, Y. (2008). Closed-form likelihood expansions for multivariate diffusions. The Annals of Statistics, 36(2), 906–937.
Aït-Sahalia, Y. y Kimmel, R. L. (2010). Estimating affine multifactor term structure models using closed-form likelihood expansions. Journal of Financial Economics, 98(1), 113–144.
Arango, L. F., Melo, L. y Vásquez, D. M. (2001). Estimación de la estructura a plazo de las tasas de interés en Colombia (Borradores de Economía No. 210). Bogotá, Colombia: Banco de la República de Colombia.
Beltratti, A. y Colla, P. (2007). A portfolio-based evaluation of affine term structure models. Annals of Operations Research, 151(1), 193–222.
Berkowitz, J. y O'Brien, J. (2002). How accurate are value-at-risk models at commercial banks? The Journal of Finance, 57(3), 1093–1111.
Brandt, M. y Chapman, D. (2003). Comparing multifactor models of the term structure. Working paper. Duke University [consultado 10 Dic 2015]. Disponible en: https://faculty.fuqua.duke.edu/mbrandt/papers/working/mfcompare.pdf
Caldeira, J. F., Moura, G. V. y Santos, A. A. (2015). Measuring risk in fixed income portfolios using yield curve models. Computational Economics, 46(1), 65–82.
Castro, G. A. y Melo, L. (2010). Relación entre variables macro y la curva de rendimientos (Borradores de Economía No. 605). Bogotá, Colombia: Banco de la República de Colombia.
Christensen, J. H., Diebold, F. X. y Rudebusch, G. D. (2009). An arbitrage-free generalized Nelson-Siegel term structure model. The Econometrics Journal, 12(3), 33–64.
Christensen, J. H., Diebold, F. X. y Rudebusch, G. D. (2011). The affine arbitrage-free class of Nelson-Siegel term structure models. Journal of Econometrics, 164(1), 4–20.
Christoffersen, P. (1998). Evaluating interval forecasts. International Economic Review, 39(4), 841–862.
Christoffersen, P. y Pelletier, D. (2004). Backtesting value-at-risk: A duration-based approach. Journal of Financial Econometrics, 2(1), 84–108.
Cox, J. C., Ingersoll, J. E., Jr. y Ross, S. A. (1985). An intertemporal general equilibrium model of asset prices. Econometrica, 53(2), 363–384.
Creal, D. D. y Wu, J. C. (2015). Estimation of affine term structure models with spanned or unspanned stochastic volatility. Journal of Econometrics, 185(1), 60–81.
Dai, Q. y Singleton, K. J. (2000). Specification analysis of affine term structure models. The Journal of Finance, 55(5), 1943–1978.
Date, P. y Bustreo, R. (2015). Value-at-Risk for fixed-income portfolios: A Kalman filtering approach. IMA Journal of Management Mathematics, 27(4), 557–573.
De Pooter, M. (2007). Examining the Nelson-Siegel class of term structure models (Tinbergen Institute Discussion Papers). Amsterdam, Holanda: Tinbergen Institute.
Diebold, F. X. y Li, C. (2006). Forecasting the term structure of government bond yields. Journal of Econometrics, 130(2), 337–364.
Diebold, F. X., Rudebusch, G. y Aruoba, B. (2006). The macroeconomy and the yield curve: A dynamic latent factor approach. Journal of Econometrics, 131(1), 309–338.
Diebold, F. X. y Rudebusch, G. D. (2011). The Dynamic Nelson-Siegel Approach to Yield Curve Modeling and Forecasting. Princeton, NJ: Princeton University Press.
Diebold, F. X. y Rudebusch, G. D. (2013). Yield Curve Modeling and Forecasting. Princeton, NJ: Princeton University Press.
Duffee, G. R. (2002). Term premia and interest rate forecasts in affine models. The Journal of Finance, 57(1), 405–443.
Duffee, G. (2013). Bond Pricing and the Macroeconomy. En G. M. Constantinides, H. Milton, y R. M. Stulz (Eds.), Handbook of the Economics of Finance (Volume 2) (pp. 907–967). Elsevier. Part B.
Duffie, D. y Kan, R. (1996). A yield-factor model of interest rates. Mathematical Finance, 6(4), 379–406.
Ferreira, M. (2005). Forecasting the comovements of spot interest rates. Journal of International Money and Finance, 24(5), 766–792.
Ferreira, M. y Lopez, J. (2005). Evaluating interest rate covariance models within a value-at-risk framework. Journal of Financial Econometrics, 3(1), 126–168.
Gomez-Restrepo, J. y Restrepo-Tobón, D. A. (2016). Estimating the Colombian yield curve using a dynamic model with macrofactors (Working Paper). Medellín, Colombia: Universidad EAFIT [consultado 10 Feb 2016]. Disponible en: http://hdl.handle.net/10784/9553.
Gürkaynak, R. S. y Wright, J. H. (2012). Macroeconomics and the term structure. Journal of Economic Literature, 50(2), 331–367.
Haas, M. (2001). New Methods in Backtesting (Working paper in Financial Engineering). Bonn, Germany: Research Center Caesar [consultado 13 Dic 2015]. Disponible en: https://www.ime.usp.br/rvicente/risco/haas.pdf
Jorion, P. (2006). Value at risk (3 rd ed). New York, NY: McGraw-Hill.
Kim, D. H. y Orphanides, A. (2012). Term structure estimation with survey data on interest rate forecasts. Journal of Financial and Quantitative Analysis, 47(1), 241–272.
Kupiec, P. (1995). Techniques for verifying the accuracy of risk management models. Journal of Derivatives, 3(2), 73–84.
Litterman, R. B. y Scheinkman, J. (1991). Common factors affecting bond returns. The Journal of Fixed Income, 1(1), 54–61.
Longerstaey, J. (1996). Mapping to describe positions (Technical Document 4 th ed.). New York: Morgan RiskMetrics.
Lopez, J. A. (1998). Methods for evaluating value-at-risk estimates. FRBNY Economic Policy Review, 4(3), 119–124.
Lopez, J. (1999). Regulatory evaluation of Value-at-Risk models. Journal of Risk, 1(2), 37–63.
Maldonado, R., Pantoja, J. O. y Zapata, N. (2015). Estimación dinámica de una estructura de tasas de interés para Colombia: Análisis empírico de filtros de Kalman. Journal of Economics & Administrative Science, 19(37), 70–77.
Martellini, L. y Meyfredi, J. C. (2007). A copula approach to Value-at-Risk estimation for fixed-income portfolios. Journal of Fixed Income, 17(1), 5–15.
Melo, L. y Granados, J. (2011). Regulación y valor en riesgo. Ensayos sobre Política Económica, 29(64), 110–177.
Nelson, C. R. y Siegel, A. F. (1987). Parsimonious modelling of the yield curves. Journal of Business, 60(4), 473–489.
Pérignon, C. y Smith, D. R. (2007). Yield-factor volatility models. Journal of Banking & Finance, 31(10), 3125–3144.
Piazzesi, M. (2010). Affine term structure models. En Y. Ait-Sahalia y L. P. Hansen (Eds.), Handbook of Financial Econometrics (pp. 691–766). New York: Elsevier.
Rezende, R. B. y Ferreira, M. S. (2011). Modeling and forecasting the yield curve by an extended Nelson-Siegel class of models: A quantile autoregression approach. Journal of Forecasting, 30(8), 339–350.
Santos, A. A., Nogales, F. J., Ruiz, E. y van Dijk, D. (2012). Optimal portfolios with minimum capital requirements. Journal of Banking & Finance, 36(7), 1928–1942.
Sousa, J. B., Esquıvel, M. L., Gaspar, R. M. y Real, P. C. (2012). Bonds historical simulation value at risk (Working paper). Lisboa, Portugal: Universidade NOVA de Lisboa [consultado 10 Ene 2016]. Disponible en: http://www.cma.fct.unl.pt/sites/www.cma.fct.unl.pt/files/documentos/publicacoes/pdf 2012/CMA%2032012.pdf
Su, E. y Knowles, T. W. (2010). Measuring bond portfolio Value at Risk and expected shortfall in US Treasury market. Asia Pacific Management Review, 15(4), 477–501.
Svensson, L. O. (1994). Estimating and interpreting forward interest rates: Sweden 1992-1994 (IMF Working Papers 94/114). Washington DC: International Monetary Fund [consultado 11 Ene 2016]. Disponible en: http://ideas.repec.org/p/imf/imfwpa/94-114.html
Trolle, A. B. y Schwartz, E. S. (2009). A general stochastic volatility model for the pricing of interest rate derivatives. Review of Financial Studies, 22(5), 2007–2057.
Vasicek, O. (1977). An equilibrium characterization of the term structure. Journal of Financial Economics, 5(2), 177–188.
Velásquez-Giraldo, M. y Restrepo-Tobón, D. A. (2016). Affine term structure models: Forecasting the yield curve for Colombia. Lecturas de Economía, 85, 53–90.
Vlaar, P. J. (2000). Value at risk models for Dutch bond portfolios. Journal of Banking & Finance, 24(7), 1131–1154.