DATOS DE PANEL EN PROBIT DINÁMICOS

JHON JAMES MORA¹

¹Economista de la Universidad del Valle. MA en Recursos Naturales y Economía de la Universidad Autónoma de Madrid. Maestría en Economía de la Universidad Alcalá de Henares. Ph.D. en Economía de la Universidad de Alcalá de Henares. Jefe del Departamento de Economía, Universidad Icesi. Cali, Colombia. jjmora@icesi edu.co

Fecha de recepción: 18-10-2005 Fecha de aceptación: 18-9-2006

RESUMEN

Este artículo discute en primer lugar dos problemas fundamentales en datos de panel: Las condiciones iniciales y la exogeneidad. En segundo lugar, muestra una aplicación al mercado laboral español de un probit dinámico para el periodo 1994-2000.

PALABRAS CLAVE

Datos de panel, probit dinámicos, mercado laboral.

Clasificación: JEL: C33, C35, J21.

ABSTRACT

This paper first provides a review of two fundamental issues of panel data, i.e. initial conditions and exogeneity. Then it presents the application of a dynamic probit to the Spanish labor market in the period from 1994 to 2000.

KEY WORDS

Panel data, dynamic probit, labor market

INTRODUCCIÓN

Aun cuando en Colombia es incipiente el uso de modelos de datos de panel, debido sin duda a la carencia de datos adecuados, tanto en Estados Unidos como en Europa su uso es muy común debido a la disponibilidad de los mismos.² Los datos de panel son muy valiosos ya que no solamente brindan información de corte transversal sino también en el tiempo sobre el comportamiento de los agentes económicos.

El planteamiento dinámico de los modelos con variables dependientes cualitativas se debe a Heckman (1981); sin embargo, la estimación de las condiciones iniciales ha generado un gran debate en torno a los supuestos requeridos. En esta vía, los desarrollos recientes que posibilitan estimar este tipo de modelos con el software econométrico existente sin mayor programación contribuirán a difundir el uso de los modelos probit dinámicos.

Este artículo hace énfasis en la discusión de dos problemas en los modelos probit dinámicos con datos de panel, a saber: El problema de las condiciones iniciales y la exogeneidad estricta. En la primera parte se discute el problema de las condiciones iniciales y su modelación a partir de la metodología de Wooldridge. En la segunda sección, se plantea el problema de la exogeneidad y se avanza en su contrastación. En la tercera sección se presenta una aplicación de la hipótesis de Carnegie con datos de panel para mujeres entre los 20 y 60 años para España. Finalmente se llega a las conclusiones.

1. EL PROBLEMA DE LAS CONDICIONES INICIALES

Heckman (1981a) plantea que uno de los principales problemas en los modelos probit dinámicos consiste en preguntarnos si el proceso puede ser explicado por una dependencia de los estados verdadera, en el sentido de que la decisión pasada entra en el modelo de una forma estructural como una variable explicativa, o puede ser debido a una dependencia de los estados espuria, es decir, como efecto de la correlación serial en las perturbaciones del modelo. Supóngase el siguiente modelo probit dinámico para datos de panel en donde existe dependencia de estado de primer orden, de la siguiente forma:

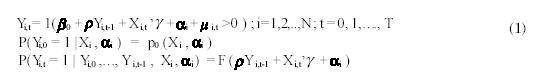
Donde Y_it es la variable de interés, 1(•) es un indicador de la función que toma valor de 1 si el fenómeno se presenta y cero de otra forma, X_it es un vector de variables exógenas, ai es el efecto específico individual que se asume invariante con el tiempo y μ_it es un término de error idiosincrático que se asume i.i.d sobre el tiempo e individuos con una función de distribución F(•). El parámetro ρ mide el grado en el cual el estado, en el último periodo, afecta directamente la probabilidad de estar en el estado en el periodo corriente y es una medida de la dependencia verdadera del estado, después de controlar por la heterogeneidad no observable α_i. Por otro lado, los efectos de los factores observados y no observados 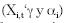capturan la heterogeneidad a través de los individuos. La contribución del logaritmo de la verosimilitud para el individuo i se puede expresar como:

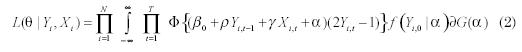
En la ecuación (2), θ es un vector de parámetros que “parametriza” totalmente el modelo y ƒ(•) es la función de distribución para los momentos iníciales condicionada a los efectos no observados.

Como se puede observar, de la ecuación (2), es necesario determinar las condiciones iniciales con el fin de obtener estimadores consistentes. Si el inicio del periodo muestral no coincide con el proceso estocástico que genera las observaciones, se hace necesario asumir el comportamiento de los valores iniciales 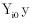, como bien muestra Hsiao (1986), supuestos diferentes con respecto a las condiciones iniciales darán lugar a funciones de verosimilitud diferentes. Obsérvese además, que ignorar la condición inicial implica ignorar .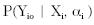

Existen tres aproximaciones comunes al problema de las condiciones iniciales: En primer lugar, se puede asumir que las condiciones iniciales son exógenas (Card y Hyslop, 2002), es decir, que Y_io es independiente de α_i. Sin embargo, si el proceso comienza en t = 0 existe una significativa heterogeneidad no observable en la población que no cumpliría con este supuesto. Asumir que las condiciones iniciales son exógenas podría sesgar hacia arriba la dependencia del estado estimada y sesgar hacia abajo la heterogeneidad estimada. En segundo lugar, se puede asumir que el proceso dinámico está en equilibro, tal vez condicionado sobre el vector de variables exógenas al comienzo del periodo muestral (Card y Sullivan, 1988). Este supuesto implica restricciones sobre los parámetros del proceso dinámico y, en particular, sobre la probabilidad del periodo inicial 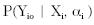. Las restricciones impuestas son menos convincentes que imponer exogeneidad sobre la condición inicial. La tercera aproximación consiste en adoptar una especificación flexible en forma reducida para el problema de la condición inicial (Heckman, 1981b). En la práctica esto implica especificar el resultado del periodo inicial en la cual ni los parámetros ni los errores se encuentren relacionados (estructuralmente) con los errores de la ecuación (1). De esta forma, la estimación del modelo podría entonces combinar la especificación anterior para los resultados del periodo inicial con la especificación estructural para el proceso dinámico de los periodos siguientes, ecuación (1). Obsérvese que la formulación de las condiciones iniciales complica bastante los cálculos computacionales del modelo.

Wooldridge (2003), por su parte, presenta una aproximación más simple al problema de las condiciones Iniciales. En particular, Wooldridge (2003) propone especificar la heterogeneidad individual no observable de la forma:³

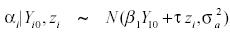
De esta forma, la verosimilitud puede reescribirse como:

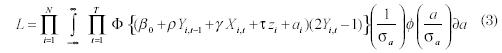
Como se puede observar de la ecuación (3) la heterogeneidad no observada se encuentra condicionada sobre las condiciones iniciales y las variables exógenas. Esto implica que, en lugar de modelar las condiciones iniciales del proceso dinámico directamente, se especifica un modelo para la heterogeneidad no observable (Wooldridge, 2003).

2. EXOGENEIDAD

La función de verosimilitud en la ecuación (3) requiere que X_i,t sea estrictamente exógena. Granger (1969) define las condiciones a través de las cuales se presenta causalidad “Y_t no causa a X_t” y Sims (1972) define las condiciones según las cuales “X_t es estrictamente exógeno”. Sin embargo, con datos de panel en los modelos probit es imposible diferenciar la heterogeneidad no observada. Siguiendo a Chamberlain (1982), la exogeneidad en modelos no-lineales se plantea de la siguiente forma: Suponga que Y_i,t es cero o uno y que se observa 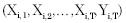para i=1,… individuos y T periodos. Entonces:

Definición 1: Causalidad de Granger X_i,t+1 es independiente de Y_i,t, Y_i,t-1 , …, condicionado sobre X_i,t , X_i,t-1, …. Para todo t.

Definición 2. Exogeneidad estricta de Sims

Por su parte, en modelos no-lineales dinámicos, la exogeneidad se puede plantear, siguiendo a Wooldridge (2000, 2002, 2003) de la siguiente forma:

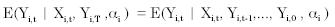
De esta forma, solamente los valores contemporáneos de X_i,t importan. Un contraste de adición implica que si X_i,t es exógena al adicionar X_i,t+1 bajo la hipótesis nula de exogeneidad X_i,t+1 no será estadísticamente significativa. Lo cual se puede contrastar con una χ²_L siendo L el número de grados delibertad igual al número de variables exógenas en X_i,t (Mora 2005).

3. APLICACIÓN AL EFECTO DE LAS HERENCIAS SOBRE LA PARTICIPACIÓN LABORAL DE LAS MUJERES EN ESPAÑA

Holtz-Eakin et al. (1993), plantean que si el ocio es un bien normal, recibir una herencia deberá disminuir la participación en el mercado laboral. Sin embargo, el modelo planteado por Holtz-Eatkin, et al. (1993), no es un modelo dinámico en el sentido estricto y, por lo tanto, no se puede conocer cómo afectan las decisiones pasadas la participación laboral en el periodo corriente.⁴

En particular, el modelo aquí planteado estimará el efecto de las herencias sobre la participación laboral de las mujeres en España, ya que aunque la participación de las mujeres en el mercado laboral español mostró un incremento sustancial a partir de los ochenta (Arellano y Bover, 1995) la tasa de participación de las mujeres sigue siendo muy inferior a la de los hombres; en el 2001 la tasa de participación se encontraba 24 puntos por debajo de la masculina y la tasa de paro doblaba a la masculina (Salido, 2002).

Los datos son tomados del PHOGUE (Panel de Hogares de la Unión Europea) para España entre 1994 y 2000 en mujeres que recibieron al menos una herencia, regalo o lotería con edades entre los 20 y 50 años en 1994. De esta forma, se seleccionaron 258 mujeres a lo largo de siete periodos para un total de 1.806 observaciones.⁴

La participación se construye como una variable dicotómica a partir de la autodefinición del estado en que se encuentra el individuo. A lo largo de los siete periodos se observa que en promedio el 75% de las mujeres está casada y que el 55% está satisfecha con el tiempo dedicado al ocio.

De igual forma, los resultados sobre la participación durante los siete años muestran, sin tener en cuenta la existencia de la heterogeneidad individual no observable, ni las variables exógenas o el periodo inicial, que existe una gran dependencia entre estados.

A continuación, suponga que Y_it es la participación en el mercado laboral si la persona recibió una herencia, regalo o lotería, 1(•) es un indicador de la función que toma valor de 1 si el individuo participa y cero de otra forma, X_it es un vector de variables exógenas, ai es el efecto específico individual que se asume invariante con el tiempo y μ_it es un término idiosincrático que se asume i.i.d sobre el tiempo e individuos con una función de distribución F(•). El parámetro ρ mide el grado en el cual el estado, en el último periodo, afecta directamente la probabilidad de estar en el estado en el periodo corriente y es una medida de la dependencia verdadera del estado, después de controlar por la heterogeneidad no observable α_i que también puede interpretarse como el coste de búsqueda. Por otro lado, los efectos de los factores observados y no observados 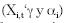capturan la heterogeneidad a través de los individuos de participar en el mercado laboral. De esta forma, el modelo planteado siguiendo a Wooldridge (2002) será:

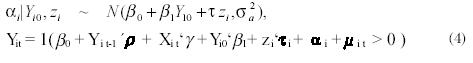
En la ecuación (4),X_i,t es un conjunto de variables que explican la participación de la mujer en el mercado laboral español. En particular, Arellano y Bover (1995) consideran que la educación universitaria es un indicador de las ganancias potenciales y Álvarez-Llorente (2002) considera que la probabilidad de participación de la mujer viene determinada fundamentalmente por el nivel educativo - a mayor nivel educativo mayor será el coste de oportunidad de no participar aumentando la probabilidad de participar. Tanto Álvarez-Llorente (2002) como Cañada (1989), Martinez- Granado (1994) y González, Pérez y Prieto (1999) encuentran un efecto positivo y significativo de la educación de la mujer sobre la probabilidad de participar. Con el fin de medir el efecto de las herencias, regalos o loterías, se incluirá en X_i,t una variable que cualifica si la persona recibió una herencia, regalo o lotería por un monto de 10.000 euros y, se espera que la recepción de las mismas disminuya la probabilidad de participar. Finalmente z_i son variables de interacción entre la tasa de desempleo de la mujer en el periodo inmediatamente anterior y el estado civil en el periodo t si ella se encontraba casada, de esta forma, los efectos individuales se encuentran correlacionados con el estado civil de la mujer y el ciclo económico. Por otro lado, la importancia de los efectos de la heterogeneidad individual no observada, en la estimación de la probabilidad de participar en el mercado laboral, se estimará como .

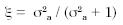En la Tabla 1 se presentarán las estimaciones del modelo 4.⁶

La segunda columna de la Tabla 1 muestra un pool probit. Las variables son estadísticamente significativas, con excepción de la dummy para 1995. De acuerdo con el pool probit, la dependencia de estado en 1995 es alrededor del 78%, sin considerar la heterogeneidad individual no observable, α_i.⁷

En la tercera columna de la Tabla 1 se calcula el modelo 4 con efectos aleatorios incluyendo solamente como variable explicatoria las herencias, regalos o loterías, la cual es significativa y con el signo esperado. Dada la significancía estadística de ε, 58.65, podemos observar que existe una relativa importancia de los efectos de la heterogeneidad individual no observada en la estimación de la probabilidad de participar. Además, usando la prueba de Wald y Lr se puede concluir, de acuerdo con el valor de la chi²(2), que las variables son estadísticamente diferentes de cero y, la varianza total del error estimada debido a la heterogeneidad no observada, a través de la muestra, fue de 1.42 y las herencias, regalos o loterías son exógenas.

4. CONCLUSIONES

En primer lugar, existen dos problemas fundamentales en los datos de panel: Las condiciones iniciales y la exogeneidad. Con respecto a las condiciones iniciales, la solución más simple parece ser la provista por Wooldridge (2002) ya que tan sólo requiere un software que tenga incorporada la estimación por efectos aleatorios. Sin embargo, a las ganancias obtenidas por esta vía deberán descontárseles los costos de exigir que el panel sea balanceado. Con respecto a la exogeneidad, Chamberlain (1982) muestra las equivalencias de las definiciones de Sims (1972) y Granger (1969) en el caso de los modelos probit. La metodología propuesta por Wooldridge (2002) requiere de exogeneidad, que puede contrastarse en forma sencilla con un contraste de adición como el aquí sugerido.

En segundo lugar, la aplicación al mercado laboral español aquí realizada de un modelo probit dinámico con datos de panel muestra que el efecto positivo y significativo de la educación de la mujer sobre la probabilidad de participar.

Por último, como plantea Hsiao (2003) todos los beneficios asociados al uso de los datos de panel van de la mano de los nuevos y difíciles problemas que deberán resolverse particularmente en los modelos no lineales.

Pié de Página

1. Agradezco los comentarios y discusiones con Jeffrey Wooldridge, a los asistentes al seminario de economía del Banco de la República en agosto del 2005 y los comentarios del evaluador anónimo. Finalmente, los errores que persisten son de mi absoluta responsabilidad.

2. La imposibilidad de tener una encuesta para Colombia que siga a los individuos en el tiempo ha llevado a que el uso de los datos de panel se haya orientado al análisis de sectores con base en la Encuesta Anual Manufacturera [para un ejemplo ver Cardona y Cano (2005)].

3. Arellano y Carrasco (2002) también plantean una estimación de máxima verosimilitud condicional sobre la condición inicial con el fin de solucionar este problema.

4. Aunque Holtz-Eatkin et al. (1993) incluyan una variable dummy que capture si el individuo participó en 1984 el modelo no deja de ser de corte transversal y, por lo tanto, es imposible determinar si existe dependencia entre estados.

5. Los datos fueron obtenidos a partir del convenio entre Eurostat y la Universidad Alcalá de Henares.

6. Agradezco los comentarios a una versión anterior de este modelo a los asistentes al Seminario de Economía del Banco de la República, en agosto de 2005.

BIBLIOGRAFÍA

1. Arellano, M. & Bover, O. (1995). Female Labour Force Participation in the 1980‚s: The Case of Spain. Investigaciones Económicas, 19(2), 171-194.

2. Arellano, M. & Carrasco, R. (2002). Binary Choice Panel Data Models with Predetermined Variables. CEMfi, W.P, No. 9618.

4. Cañada, J.A. (1989). Oferta de trabajo de las mujeres en España: Evolución y prospectivas. Servicio de Estudios de la CAIXA, Colección de estudios e informes.

5. Card, D. & Hyslop, D. (2002). Estimating the Dynamic Treatment Effects of an Earnings Subsidy for Welfare Leavers, UC Berkeley, Center for Labor Economics, W.P, N. 47.

6. Card, D. & Sullivan, D. (1988). Measuring the Effect of Subsidized Training Programs on Movements in and Out Employment. Econometrica, 56, 497-530.

7. Cardona, M y Cano, C.A. (2005). La dinámica industrial, crecimiento económico y PyMEs: Un análisis de Datos de Panel para el caso colombiano 1980-2001, Archivos de Economía, 292, D.N.P.

8. Carnegie, A. (1891). The Advantages of Poverty, In The Gospel of Wealth and Other Timely Essays, Edward C. Kirkland (Eds). (Harvard University Press 1962)

9. González, I., Pérez, C., y Prieto, M. (1999). La participación laboral de la mujer en Castilla y León. Revista de Investigación Económica y Social de Castilla y León 2, 83-98.

10. Heckman, J. (1981a). Statistical Models for Discrete Panel Data, Chapter 4 in Manski, Ch and D. MacFaden (Eds), Structural Analysis of Discrete Data, MIT Press.

11. Heckman, J. (1981b). The Incidental Parameters Problem and the Problem of Initial Conditions in Estimating a Discrete Time- Series Data Stochastic Process, Chapter 4 in Manski, Ch and D. MacFadden (Eds), Structural Analysis of Discrete Data, MIT Press.

12. Holtz-Eakin, D., D. Joulfaian, H.S. Rosen. (1993). The Carnegie Conjecture: Some Empirical Evidence, The Quarterly Journal of Economics, 108, 413-435.

13. Hsiao, Ch. (2003). Analysis of Panel Data, (Second Edition) Cambridge University Press.

16. Wooldridge, J.M. (2003). Simple Solutions to the Initial Conditions Problem in Dynamic, Nonlinear Panel Data Models with Unobserved Heterogeneity, Mimeo Department of Economics, Michigan State University.