ARTÍCULOS

Modelos de valoración de opciones sobre títulos de renta fija: aplicación al mercado colombiano¹

Fixed income option pricing models: application to the colombian market

Modelos de avaliação de opiniões sobre títulos de renda fixa: aplicação ao mercado colombiano

Luis Guillermo Herrera Cardona ^a, Darwin Cárdenas Giraldo^b

^aDirector Científico y de Investigaciones, Global Capital Management, Colombia. Docente e investigador (GEOS), Universidad de San Buenaventura, Cali, Colombia

^bDirector de Inversiones, Global Capital Management, Colombia

Autor para correspondencia: Calle 1B Oeste # 4 A Oeste - 201 Apto. 904 Torre G, Normandía, Cali, Colombia Correo electrónico: herreracardona@gmail.com (L.G. Herrera Cardona).

Historia del artículo:
Recibido el 13 de diciembre de 2011
Aceptado el 22 de marzo de 2013

Resumen

Este documento tiene como propósito evaluar la aplicabilidad del modelo de tasa de interés de Vasicek (1977) para la valorar opciones call y put sobre un título de renta fija colombiano. Para el desarrollo de esta aplicación, se efectúan estimaciones econométricas con procesos autorregresivos y de volatilidad necesarias para encontrar los parámetros de entrada del modelo. En el avance del trabajo se encuentra que este no arroja resultados satisfactorios para las opciones sobre bonos colombianos, debido al alto valor de las primas. Sin embargo, ajustando el modelo con parámetros basados en criterios empíricos, se obtienen cifras más consistentes.

Palabras Clave: Modelos de evolución de tasas de interés, Velocidad de reversión, Modelo de Vasicek, Valoración de opciones call y put, Modelo Black-76.

Clasifiación JEL: E43, G12, G13

Abstract

This paper is to evaluate the applicability of the Vasicek (1977) model of interest rate for valuing call and put options on a fixed income Colombian security. For the development of this application are made, some econometric estimation with volatility and autoregressive processes, these are necessary to find the model input parameters. The progress of the model. Later on in the work finds that the model does not give satisfactory results for options on Colombian bonds due to the high value of premiums. However, by adjusting the model parameters based on empirical criteria consistent figures are obtained.

Keywords: Interest rate evolution models, Speed of reversion, Vasicek model, Call and put option pricing, Black-76 model.

JEL Clasification: E43, G12, G13

RESUMO

Este documento tem como propósito avaliar a aplicabilidade do modelo de taxa de juro da Vasicek (1977) para avaliar opções call e up sobre um título de renda fixa colombiano. Para o desenvolvimento desta aplicação efectuam-se estimativas econométricas com processos auto-regressivos e de volatilidade necessárias para encontrar os parâmetros de entrada do modelo. No avanço do trabalho percebe-se que o modelo não traz resultados satisfatórios para as opções sobre bonificações colombianas devido ao alto valor dos bens. Porém, ajustando o modelo com parâmetros baseados em critérios empíricos, obtêm-se valores mais consistentes.

Palavras-Chave: Modelos de evolução de taxas de juro Velocidade de regresso Modelo de Vasicek Avaliação de opções Call e put Modelo Black-76

Classificação JEL: E43, G12, G13

1. Introducción

En 2011, el mercado de capitales colombiano se caracterizaba por tener el 93,91% concentrado en títulos de renta fija, frente a un 2,41 y un 1,25% en renta variable y derivados, respectivamente². Esto indica la relevancia de contar con instrumentos de cobertura sobre activos financieros de deuda para mitigar los riesgos de tasa de interés. La realidad evidencia que Colombia es un país con un incipiente mercado de derivados y peor aún, carece de metodologías para abordar el tema específico en valoración de opciones sobre títulos de deuda y tipo de interés. No obstante, de acuerdo con Ramírez (2007), la Bolsa de Valores de Colombia adoptó la metodología de Nelson & Siegel (1987) para modelar tasas de interés y sobre esta base valorar precios futuros.

De esta manera, se hace necesaria la aplicación de modelos existentes para valorar este tipo de instrumentos derivados (opciones) sobre tasa de interés, y en esa vía introducir productos financieros presentes en otros mercados en aras de impulsar el mercado de derivados en Colombia. En general, como respuesta a dicha necesidad se podría sugerir la revisión y uso de los modelos de evolución de tasas de interés. Tal como lo exponen Restrepo & Botero (2008), en etapas incipientes de desarrollo de los mercados de derivados, estos modelos aparecen como una elección imprescindible debido a su sencillez y parsimonia.

Para el caso específico de Colombia, a partir de 2002 se comienzan a vislumbrar estudios relacionados con estructura a plazos, en donde se encuentran los trabajos de Arango, Melo & Vásquez (2002), Julio, Mera & Revéiz (2002), y Melo & Vásquez (2002). Cinco años después, se exponen documentos que incorporan la metodología de Nelson, Siegel & Svensson como el de Ramírez (2007) y posteriormente tratados alusivos al uso de modelos de tasa corta tales como el de Hull & White (1993a, 1993b), y Black & Karasinski (1991) evidenciados en Restrepo & Botero (2008) y Grajales & Pérez (2008).

Para este documento se seleccionó el modelo de Vasicek (1977). Este, además de ser pionero dentro de las metodologías de estructura a plazos, es usado en otros mercados. El modelo en mención se implementa numéricamente evolucionando la tasa de interés y finalmente valorando una opción a través de la fórmula modificada de Black (1976).

Acto seguido, se exhibe una aplicación para un título de deuda pública nacional, específicamente hablando, un TES con vencimiento al 24 de julio de 2020. Para tales efectos, se implementa una formulación en la hoja electrónica Excel 2007^® complementada por un algoritmo de programación en Visual Basic y procedimientos econométricos para estimar los parámetros de entrada que exige el modelo en EViews 5.0^®.

Como resultado de esta implementación, se encuentra que la metodología arroja resultados no satisfactorios. En otras palabras, el modelo no se ajusta a valores consistentes, porque los precios de las primas son muy elevados. Por otro lado, si se realiza el ejercicio introduciendo parámetros basados en criterios empíricos (ensayo y error) basados en otros trabajos, los resultados son satisfactorios y totalmente coherentes.

El documento presenta la siguiente estructura. En primer lugar, se hace una revisión de literatura relacionada con los modelos de evolución de tasas de interés, especificando cómo estos sirven de insumo en la determinación del valor de una opción sobre títulos de renta fija. En segundo lugar, se describe la metodología llevada a cabo en este estudio, teniendo en cuenta que se modelarán 2 escenarios, uno con estimaciones econométricas y otro con parámetros sugeridos en estudios similares. Finalmente, se presentan los resultados e interpretaciones de los resultados obtenidos, realizando un análisis específico para el caso de Colombia.

2. Marco teórico

2.1. Modelos de evolución de tasas y el trabajo de Vasicek

Los modelos de tasa de interés, también, conocidos como modelos de estructura a plazos³, están basados en teorías concernientes al comportamiento de las tasas de interés. Tales modelos buscan identificar elementos o factores que pueden explicar la dinámica de estas. Dichos factores son aleatorios o estocásticos, lo que implica que sus valores futuros no pueden ser pronosticados con certidumbre. Por lo tanto, los modelos en mención utilizan procesos estadísticos para describir las propiedades estocásticas de los factores y de este modo llegar a una representación razonablemente precisa del comportamiento de la tasa.

Los primeros modelos descritos en la literatura académica explican el comportamiento de la tasa de interés en términos de la dinámica de una tasa corta⁴. Esta estructura se refiere a la tasa de interés para un período que es infinitesimalmente pequeño.

El punto de partida en esta temática fue marcado por el trabajo de Itô (1951), el cual se exhibe en la ecuación diferencial estocástica (1):

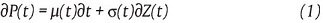
donde P(t) se refiere al precio, µ(t) es la media, σ(t) la volatilidad y Z(t) es un movimiento Browniano⁵.

A partir del teorema en mención se realiza una extrapolación al plano de las tasas de interés. De esta manera, surgen los modelos de evolución de tasas. De acuerdo con Restrepo & Botero (2008), estos se pueden clasificar en modelos de equilibrio y de no arbitraje; los primeros se basan en una serie de supuestos referentes a la economía en la cual operan y derivan un proceso para la tasa de interés de corto plazo. En dichos modelos las estructuras a plazos de tipos de interés y de volatilidades se determinan de forma endógena. Aquí se pueden referenciar trabajos como los de Vasicek (1977) y Cox, Ingersoll & Ross (1985). Por otro lado, los de no arbitraje tratan las estructuras antes mencionadas como exógenas, procurando que los precios de los títulos dados por el modelo coincidan con los observados en el mercado. En este plano se pueden resaltar los trabajos de Ho & Lee (1986), Hull & White (1990), Black, Derman & Toy (1990), Heath, Jarrow & Morton (1990) y Black & Karasinski (1991).

Otra manera de clasificar los trabajos de tasa de interés es de acuerdo con el número de factores aleatorios objeto de análisis. Mientras los modelos unifactoriales contemplan la tasa corta de interés como único factor de relevancia, aspecto que los hace débiles; los modelos multifactoriales asumen por lo menos 2 factores relevantes en su estructura a plazos de las tasas de interés, por ejemplo, la tasa corta y su tendencia, la cual sigue un proceso de Gauss-Wiener⁶. Con respecto a esta última caracterización se pueden mencionar los trabajos de Brennan & Schwartz (1979), Extended Cox-Ingersoll-Ross (CIR) en Chen & Scott (1992), y el de Heath, Jarrow & Morton (1992).

Entre tanto, el planteamiento de Vasicek fue el primer modelo de estructura a plazo descrito en la literatura académica. Es un modelo de tasa corta unifactorial de equilibrio que asume que dicha tasa es un proceso que sigue una distribución normal incluyendo unareversión a su nivel medio.

El modelo es muy popular en los círculos académicos y en los laboratorios de mercados financieros dado que es analíticamente tratable y fácil de implementar. A pesar de que tiene un elemento de volatilidad constante, la reversión a la media elimina la certeza de presentar tasas de interés negativas en el largo plazo. No obstante, al no librarse del arbitraje (por no tratarse de un modelo de noarbitraje) respecto a los precios de los bonos en el mercado, algunos profesionales no trabajan con el modelo para evitar este tipo de situaciones.

El modelo de Vasicek describe la dinámica de la tasa corta deinterés y satisface el proceso de Itô dado en (2)

donde

a: velocidad de reversión a la media, es decir, la rapidez con que la tasa de interés de corto plazo tiende a regresar a su valor de largo plazo, b, una vez que se ha desviado de este.
b : nivel medio de reversión de r o tasa promedio de interés a largo plazo.
z : proceso de Wiener estándar con media 0 y desviación estándar 1.
σ : volatilidad de los cambios de la tasa de interés de corto plazo. dt : intervalo de tiempo que tiende a cero (0).
dz : es un proceso browniano.

A su vez, la dinámica de la tasa de interés dada en (2), tal y como lo interpretan Restrepo & Botero (2008), implica que los cambios en la tasa corta se componen de una tendencia dada por [a(b - r)dt] y de un componente estocástico σdz.

En otros textos se usan diferentes notaciones, presentando la fórmula (2) como:

o

De esta manera, y partiendo de (2), el precio en el tiempo t de un bono cero cupón que paga una unidad monetaria y madura al tiempo T está dado por (5)⁷.

Siendo

r(t): tasa de corto plazo en el tiempo t

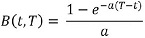
^y

En cuanto a la estructura a plazos en Vasicek (1977), siempre que la ecuación (5) se exhiba como P(t,T)=e^-(tRT)(T-t), donde _tR_T es la tasa de interés en el tiempo t para el plazo de (T - t), se obtiene:

En el modelo de Vasicek, la tasa corta r se distribuye normalmente. Por lo tanto, esto implica una probabilidad de que la tasa sea negativa, lo que no tiene sentido desde el punto de vista económico. Sin embargo, este inconveniente no lo descalifica absolutamente, ya que tal y como lo mencionan Longstaff & Schwartz (1992), y Lamothe (2003), la probabilidad de que eso ocurra es muy pequeña con unos parámetros realistas y, debido a que el valor inicial de los tipos es positivo, el valor esperado de los mismos seguirá siendo mayor que cero.

Los parámetros a y b se pueden estimar mediante una regresión debido a que este modelo supone que la tasa corta de interés sigue un proceso AR(1)⁸ tal como se explica en (7).

donde

De otra manera, la expresión (7) podría reescribirse como en (8).

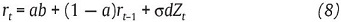
siendo

Por otro lado, la volatilidad σ puede ser estimada mediante un modelo GARCH(p,q)⁹, donde p y q pueden tomar el máximo valor de 1, en general, el modelo puede ser descrito como en (9).

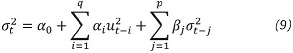
Siempre que

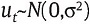
2.2. El valor de prima de la opción

En 1976, Fisher Black presentó una versión modificada del modelo convencional Black-Scholes, usando supuestos similares para valorar opciones sobre contratos a plazo. Desde entonces, el modelo se conoce como Black-76. Hoy los bancos emplean esta versión modificada para valorar swaptions¹⁰ e instrumentos similares. De igual manera, se ha conocido su empleo para opciones sobre bonos y de tipo de interés, tales como caps¹¹ y floors¹². De tal forma que las opciones sobre bonos pueden ser tratadas como opciones sobre contratos futuros de bonos. Para tal efecto, el académico adaptó las ecuaciones genéricas cambiando la nomenclatura de algunas variables y haciendo cambios estructurales, tal y como se muestran en (10) y (11).

En donde,

N(d₁), N(d₂), N(-d₁) y N(-d₂) son parámetros de normalidad (distribución normal estándar acumulada en d_i),

F es el precio forward del bono subyacente en el momento t; K es el precio de ejercicio o strike; σ es la volatilidad del precio forward y T es el vencimiento del contrato a plazo. P(t,T), B(t,T), y A(t,T) son variables de salida del modelo de Vasicek (1977), los cuales se tratan en la sección 2.1. Cuando t y T toman el valor de cero en las expresiones anteriores se generan los términos P(0,T), P(t,0), B(0,T), B(t,0), A(0,T) y A(t,0).

3. Metodología y datos para la aplicación

Para este trabajo, se tomaron como referencia los bonos emitidos por la Tesorería Nacional con vencimiento al 24 de julio de 2020, TFIT15240720¹³, por ser los títulos con más volumen de negociación y con más liquidez del mercado a la fecha. El rango de datos va desde el 5 de agosto de 2005, fecha en la cual empezaron a cotizar en pantalla, hasta el 5 de noviembre de 2010. Con la serie de datos obtenidos de los cierres diarios en el intervalo de fechas mencionadas se presentarán 4 escenarios de vencimiento para las opciones call y put, el primero a 15 días, el segundo a 30 días (1 mes), el tercero a 180 días (6 meses) y finalmente a 360 días (1 año).

Para este caso, los parámetros de entrada que tomará el modelo (2) se estimarán mediante procedimientos econométricos, cuyos resultados se presentarán en la siguiente sección. La velocidad de reversión a la media a y la tasa de largo plazo b se estimarán mediante un proceso AR(1); mientras que para la volatilidad σ se correrá un proceso GARCH(1,1). Lo anterior de acuerdo a los supuestos planteados en el modelo de Vasicek descritos en la sección 2, específicamente en las expresiones (7) y (9).

Por otra parte, r₀ o tasa de interés cuando t es igual a cero (0), es decir, en el momento de realizar la valoración, tomará el valor de 7,08%, cifra que corresponde al rendimiento actual del mercado para el TES escogido.

t : es la maduración de la opción para el bono, la cual será analizada mediante los 4 escenarios especificados al inicio de esta sección.

T : es la maduración del bono, que para este caso es aproximadamente igual a 9,6932 desde la última cotización analizada en este trabajo, es decir el 5 de noviembre de 2010.

Es de aclarar, y como ya se mencionó anteriormente, que el bono fue emitido el 24 de julio de 2005 con un horizonte a la fecha de 15 años, es decir, con un vencimiento al 24 de julio de 2020, por lo tanto, el tiempo restante de caducidad es el anteriormente citado.

Para realizar análisis adicionales, también se tomarán parámetros ficticios o empíricos (a tomará el valor de 0,06). Para contrastar la veracidad de la escogencia, Hull (2006), Choudhry (2005), y Brigo & Mercurio (2006) coinciden en asumir este valor; asimismo lo sugieren Grajales & Pérez (2008), en el caso de una aplicación a un título colombiano.

Entre tanto, la tasa de largo plazo, b, tomará el valor de 0,0581. Si bien es cierto, este parámetro también es constante, también cabe resaltar que al ser una función del tiempo, permite ajustar el modelo a cualquier estructura a plazos de tasa de interés, es por eso que de acuerdo con el valor que tome el strike, de igual manera se debe ajustar este parámetro. En este aspecto, también coinciden Grajales & Pérez (2008).

Finalmente, la volatilidad, σ, se calculará con una ventana de estimación que dependerá de la maduración t de la opción, tal y como los sugiere Lamothe (2003).

Las demás variables de entrada no tomarán valores diferentes alos anteriormente especificados.

4. Resultados y discusión

4.1. Estimación de los parámetros a y b

Tal y como se explicó en la sección 2.1, debido a que el modelo de Vasicek asume un proceso AR(1) para las tasas de interés, es necesario realizar una prueba de estacionariedad antes de estimar los parámetros. Los resultados se pueden evidenciar en la tabla A1 de los anexos.

Las pruebas antes mencionadas evidencian que la serie de la tasa de intereses no estacionaria en su nivel, mientras que en su primera diferencia, sí lo es. Por tal razón, la serie de los tipos de interés para el título valor seleccionado demanda el uso de tratamientos estadísticos adicionales para efectos de análisis econométricos.

Teniendo claro el procedimiento previo, los coeficientes del modelo descrito en (7) resultantes de modelar el proceso AR(1), los cuales se describen en la tabla A2 (anexos) se deben transformar en términos del modelo (2). De esta manera:

Según las cifras arrojadas por los cálculos, se evidencia que la velocidad con la cual los rendimientos del bono TFIT15240720 revierten a su media es alta (0,6552). Esto supone que una vez la tasa de interés del título analizado se aleja de su nivel de largo plazo 7,95% tardaría aproximadamente 1,06 años para recorrer la mitad de la brecha que la separa de su nivel de reversión¹⁴.

4.2. Estimación de la volatilidad σ

Partiendo de la expresión (9) y la estimación de los parámetros exhibidos en la tabla A3 (anexos) la volatilidad requerida en Vasicek será la siguiente:

De esta manera, y de acuerdo con Restrepo & Botero (2008), se calibra el modelo, ante la ausencia de información histórica sobre opciones en Colombia, más aún para el TES.

4.3. Valoración de las opciones call y put

El valor de las opciones call y put a partir de los parámetros estimados econométricamente no arrojan resultados satisfactorios, dado que son muy altos, aspecto que los aleja de la realidad. En la tabla 1 se puede evidenciar que para una tasa de interés que se ha mantenido en promedio en 7,04% efectivo anual (e.a) en las últimas 2 semanas (teniendo en cuenta la fecha de valoración), la tasa strike calculada a partir del modelo es de 7,1% e.a., en una opción con vencimiento a 15 días, la prima call es de 0,00635 (132,78 en precio y en tasa 6,37%) y la put es de 0,00633 (122,38 en precio y en tasa 7,63%). Para una mejor comprensión gráfica, en las figuras 1 y 2 se puede observar la sensibilidad de las primas call y put ante cambios en la volatilidad y la velocidad de reversión.

Una posible explicación sobre la no conformidad de los resultados podría corresponder a que i) las estimaciones llevadas a cabo a partir de los parámetros a, b y σ estimados econométricamente no fueron las mejores para el mercado colombiano, y ii) por trabajar con una volatilidad relativamente alta, teniendo en cuenta que dicha volatilidad se estimó igualmente, mediante un método econométrico. De hecho, la segunda explicación podría ser consecuencia de la primera.

Ante esta afirmación, se debe tener en cuenta que el modelo econométrico se basa en la historia de la serie de tiempo de los tipos de interés, por lo tanto, no posee la capacidad de evidenciar cambios estructurales ocasionados por otras variables de la economía que impactan directamente las expectativas de movimiento de la serie a futuro.

A pesar del inconveniente, los resultados de este estudio coinciden con los encontrados por Restrepo & Botero (2008), quienes utilizaron los modelos de estructura temporal unifactorial de Hull & White (1990), y Black & Karasinski (1991) para aplicaciones en títulos colombianos. Finalmente, ellos concluyen que la estimación de la velocidad de reversión basada en parámetros econométricos no fue satisfactoria, motivo por el cual se vieron en la necesidad de asumir valores sugeridos en otras literaturas y continuar en otros frentes de su investigación. Por otro lado, Grajales & Pérez (2008) en el caso de la valoración de 2 bonos corporativos con opción call embebida de ISA (Colombia) mediante la metodología de Hull & White (1990), igualmente asumen los parámetros iniciales del modelo con valores referenciados por otros autores por inconsistencias en estimaciones econométricas y la ausencia de métodos de calibración.

De acuerdo con lo anterior, ¿qué posibles cambios de tipo econométrico podrían resolver el problema o mejorar la situación? Para este caso, se considera que ninguna modificación lo remediaría. El modelo de Vasicek (1977), por definición, supone un proceso autorregresivo de orden uno (AR[1]) para la tasa de interés, esto quiere decir que si se realizaran estimaciones de orden superior o de tipo ARMA(p,q), se desvirtuaría el modelo y perdería toda su validez. Si se hiciera una prueba con un proceso AR(p), con p = 2, 3..., para la evolución de los rendimientos del título estudiado, los parámetros de entrada a y b serían negativos, argumentos matemáticamente lógicos, pero ilógicos desde la perspectiva de las necesidades de este estudio.

Pese a los resultados, y en aras de enriquecer el análisis, se consideró pertinente asumir unos parámetros basados en criterios empíricos, los cuales se abordarán más adelante en esta misma sección.

Para dar una mayor claridad a los datos que arroja la tabla 1, se tomará como escenario de análisis el vencimiento a 30 días. En este contexto, el título se negocia a un precio de 127,35. Según los resultados econométricos, el strike sería del 126,54 (in the money para una call), lo cual supone que el comprador como mínimo debe pagar 6,95 puntos básicos (pb) de prima (diferencial entre strike y spot en tasa) más la prima de lo que el mercado estima, podría ser la volatidad en 30 días. Si la prima total de la opción call fue de 88,8 pb menos los 6,95 pb del diferencial de la call in the money, la prima asignada según el modelo por una volatilidad de 30 días sería de 81,85 pb, la cual evidentemente resulta muy costosa e improbable según los datos estadísticos del título. Lo que significa esto en dinero es que si se tiene la percepción de que la tasa del título va a caer desde su nivel actual (de otro modo, el precio del título sube), para un título con valor nominal de 500 millones de pesos y valor actual de 635,42 millones de pesos (valor nominal del título por el precio), el comprador debe pagar una prima de 48,64 millones de pesos, lo que representa pagar una prima del 7,64% para un vencimiento de 30 días, es decir, un porcentaje e.a del 141,87%, lo cual y como se mencionó anteriormente no corresponde a la realidad de un mercado eficiente. Sin embargo, se podría preguntar, ¿entonces, qué es un mercado eficiente para este producto? Para responder a esta pregunta y realizar las comparaciones respectivas de los anteriores cálculos, es necesario remitirse a la cotización de Opciones de la Nota del Tesoro Americano a 10 años cuyo nemotécnico es ZNH1 con vencimiento a 30 días (11 de febrero 11 de 2010) cuyas características se evidencian en la tabla 2.

De acuerdo con la tabla 2, la prima que se cotiza para este título (cuyas características en términos de la opción son muy similares a las del título estudiado en este documento) equivale a un 0,55% mensual o del 6,8% e.a en dólares. Si se lleva esta tasa a pesos por devaluación, resultaría una tasa del 1,29%, la cual es muy baja debido al efecto revaluacionista que tuvo el peso colombiano en 2010. Pero si se ajusta esta tasa de manera que se adicionen los pb del riesgo país medidos por el Emergency Markets Bond Index (EMBI), que para el caso de Colombia está alrededor de 110 pb, resultaría una tasa en pesos del 7,9% anual.

La tasa anual ajustada en pesos de la prima de una opción a 30 días, de un título que se transa en un mercado más desarrollado y líquido (7,9%), es mucho más acertada de acuerdo con la estructura de tasas en el mercado para la época y dista enormemente de la tasa arrojada por el modelo, cuyos cálculos fueron basados en parámetros econométricos (141,87%).

Entre tanto, en otro frente del análisis, las figuras 1 y 2 muestran que el valor de una opción call al igual que el de una put incrementa conforme aumenta la volatilidad y disminuye la velocidad de reversión a la media. En otras palabras, el valor de la prima de una opción sobre títulos de renta fija es mayor mientras más varíe su rendimiento (tipo de interés) y menor sea el retorno de la tasa a su nivel medio de largo plazo. Este comportamiento es independiente de la consistencia en los resultados obtenidos.

Por otra parte, una desventaja observada en el modelo es que no permite ajustes en el strike, dado que Vasicek (1977) lo contempla como una variable de salida. En la realidad, las negociaciones con opciones incluyen la fijación de un precio strike.

De manera complementaria, si se consideran los ajustes en los parámetros a, b y σ citados en la sección 3 y anteriormente en esta misma sección, y basados en criterios empíricos llevados a cabo en trabajos anteriores, cuyos autores ya se mencionaron (en la misma sección 3), los resultados son más satisfactorios para el mercado colombiano (tabla 3).

Analizando los resultados de la siguiente tabla, para el vencimiento a 30 días, se puede observar que, en este caso, el valor que se ha de pagar por la prima equivale a un 1,14% mensual o un 14,57% e.a, lo que resulta más consistente y coherente con la estructura de tasas para el mercado colombiano y aún más, teniendo en cuenta que no hay una justa formación de precios.

Las anteriores cifras estimadas por el modelo y basadas en parámetros predeterminados, podrían servir de referente para la formación precios de los títulos de renta fija que se negocian en el mercado. Los valores de las primas de una call con los 4 escenarios de vencimiento estudiados no son tan descabellados como ocurrió en los resultados arrojados por la tabla 3.

5. Conclusiones y recomendaciones

En esta investigación se estimaron los valores de las opciones call y put para un bono del Gobierno colombiano con vencimiento en 2020, por medio del modelo de evolución de tasa corta de Vasicek. Para llegar a este punto, se implementó la siguiente ruta:

• Estimación econométrica de los parámetros de entrada: velocidad de reversión a y tasa de largo plazo b a través de un proceso AR(1).
• Estimación econométrica de la volatilidad σ mediante un proceso GARCH(1,1).
• Estimación de la evolución de la tasa de interés utilizando el modelo de Vasicek mediante un algoritmo en Visual Basic en la hoja electrónica Excel.
• Cálculo del valor de las primas de las opciones call y put usando el modelo de Black-76 mediante un algoritmo en Visual Basic en la hoja electrónica Excel.

Para las estimaciones de los parámetros a, b y σ, fue necesario el uso del software EViews 5.0^®. Igualmente, para la evolución de las tasas de interés y el cálculo de las primas de las opciones, fue necesario implementar un algoritmo de programación en Visual Basic mediante la hoja electrónica Excel 2007^®. Finalmente, en este último programa, se realizaron los análisis de sensibilidad que posibilitaron los razonamientos pertinentes.

Los resultados que se obtuvieron a partir de los parámetros estimados econométricamente no fueron los mejores, por lo tanto, el valor de las opciones no permitieron realizar del todo análisis objetivos. Sin embargo, cuando dichos parámetros se ajustaron manualmente basados en criterios empíricos, las cifras se tornaron más satisfactorias.

Los resultados del trabajo permiten realizar aportes importantes en el proceso de maduración en el tema del uso de instrumentos derivados sobre tipos de interés en Colombia.

Para efectos de investigaciones futuras, se podría abordar la aplicación de una metodología para valorar opciones americanas sobre tipos de interés, incluyendo árboles binomiales mediante el modelo unifactorial de Vasicek (1977) u otros modelos de similares características, o tal vez más sofisticados.

Notas

¹ Este documento es el producto del proyecto de investigación de grado presentado para optar al título de Magíster en Finanzas, otorgado por la Universidad ICESI, Cali, Colombia, en convenio con el Stuart School of Business, Illinois Institute of Technology, Chicago, Illinois, EE. UU. Igualmente, ha sido resultado del estudio sobre ''riesgo y valor en el sistema financiero colombiano'' por los autores, cuyo proyecto de investigación se viene desarrollando en el grupo GEOS de la Universidad de San Buenaventura seccional Cali.

² Cifras a 31 de diciembre de 2010, extraídas del informe anual de la Bolsa de Valores de Colombia, consultado el 19 de enero de 2011.

³ Atendiendo a Arango et al. (2002) una estructura a plazo de tasa de interés es una relación entre los rendimientos y los períodos de maduración de títulos con similar calidad crediticia, regularmente libres de riesgo. A la representación gráfica de esta estructura se le conoce como curva de rendimientos (yield curve).

⁴ En una literatura más técnica, tasa de interés de corto plazo.

⁵Un movimiento Browniano es un proceso estocástico surgido en el escenario de la física-química que explica el comportamiento aleatorio en el movimiento de las partículas en un fluido, el concepto fue adaptado a la economía y las finanzas para describir la dinámica probabilística de los precios de los activos financieros.

⁶ Estrictamente hablando, un proceso de Gauss-Wiener se refiere a un movimiento browniano, el cual se describió en la nota anterior.

⁷ Para mayor profundización, remitirse a Vasicek (1977) y ver la sección 5.3 en Van Deventer e Imai (1997).

⁸ Quiere decir que la tasa corta se comporta como una serie autorregresiva cuyo rezago máximo es la tasa del período inmediatamente anterior. En otras palabras, el valor de las tasas cortas futuras depende de la tasa misma.

⁹ Un proceso Generalised Autoregressive Conditionally Heteroskedasticity o GARCH mide el grado de variabilidad presente en una serie de tiempo y estima las variaciones futuras a partir de sus datos históricos. Bajo un modelo GARCH(p,q), la volatilidad se concibe como una composición de una parte residual y otra parte explicada a partir de su variación histórica, donde p y q indican los rezagos máximos tanto en sus varianzas como en sus residuos, respectivamente. Por fortuna, generalmente un modelo GARCH(1,1) será suficiente para solucionar el problema de volatility clustering presente en las series, basados en Brooks (2008).

¹⁰ Un Swaption es un derivado financiero consistente en una opción cuyo subyacente es un swap, normalmente un interest rate swap (IRS). Es decir, ofrece la posibilidad de entrar en una permuta de tipo de interés.

¹¹ Un cap es un instrumento de gestión de riesgo del tipo de interés a medio y largo plazo que consiste en un acuerdo entre dos partes mediante el cual un prestatario se asegura el tipo máximo que se le aplicará a un préstamo a cambio del pago de una prima.

¹² Un floor es lo contrario a un cap, en este contrato el comprador se asegura la rentabilidad mínima de un depósito a cambio de una prima.

¹³ Este título es emitido por la Tesorería del Gobierno Nacional, vence a la fecha especificada y no paga cupones.

¹⁴ El mismo análisis es abordado por Restrepo & Botero (2008), basados en Tuckman (2002), quien argumenta que es posible mostrar que la distancia entre el valor actual de una variable y su nivel de reversión de largo plazo decae exponencialmente a una tasa igual a la velocidad de reversión. Con frecuencia, este análisis se cuantifica mediante el indicador half-life, HL = ln(2)/a, siendo a la velocidad de reversión. Dicho indicador explica cuánto tarda una variable en recorrer la mitad de la distancia que la separa de su nivel de largo plazo.

Bibliografía

Arango, L. E., Melo, L. F. & Vásquez, D. M. (2002). Estimación de la estructura a plazo de las tasas de interés en Colombia. Banco de la República. Borradores de Economía, 196.

Black, F. (1976). The pricing of commodity contracts. Journal of Financial Economics, 3, 167-179.

Black, F., Derman, E. & Toy, W. (1990). A One-factor model of interest rates and its applications to treasury bond options. Financial Analyst Journal, 46, 33-39.

Black, F. & Karasinski, P. (1991). Bond and option pricing when short rates are lognormal. Financial Analyst Journal, 47, 52-59.

Bolsa de Valores de Colombia (2011). Informe Anual, Mercados de la BVC 2010. Recuperado el 19 de enero de 2011, de http://www.bvc.com.co/pps/tibco/portalbvc/Home/Mercados/informesbursatiles

Brennan, M. & Schwartz, E. (1979). A continuous approach to the pricing of bonds. Journal of Banking and Finance, 35, 405-417.

Brigo, D. & Mercurio, F. (2006). Interest rate models - theory and practice with smile, inflation and credit. (2.^a ed.). Berlín: Springer Verlag.

Brooks, C. (2008). Introductory Econometrics for Finance (2.^a ed.). Nueva York: Cambridge University Press.

Chen, R. & Scott, L. (1992). Pricing interest rate futures options with futures-style margining. The Journal of Futures Markets, 13, 15-22.

Choudhry, M., (2005). Fixed income securities and derivatives handbook, analysis and valuation. Princeton: Bloomberg Press.

CME Group. Interest Rates Options Product Slate. Recuperado el 10 de enero de 2011, de http://www.cmegroup.com/education/options.html

Cox, J. C., Ingersoll, J. E. & Ross, S. A. (1985). A Theory of the Term Structure of Interest Rates. Econométrica, 5(2), 385-408.

Grajales, C. A. & Pérez, F. O. (2008). Modelo de tasa corta de Hull y White y valoración de bonos con opción call. Universidad de Medellín.

Heath, D., Jarrow, R. & Morton, A. (1990). Bond pricing and the term structure of interest rates: a discrete time approximation. Journal of Financial and Quantitative Analysis, 25, 419-440.

Heath, D., Jarrow, R. & Morton, A. (1992). Bond pricing and the term structure of interest rates: a new methodology for contingent claims valuation. Econométrica, 60, 77-105.

Ho, T. & Lee, S. (1986). Term structure movements and pricing interest rate contingent claims. Journal of Finance, 41, 1011-1029.

Hull, J. (2006). Options, futures and other derivatives (6.^a ed.). Toronto: Prentice Hall.

Hull, J. & White, A. (1990). Pricing interest-rate- derivative securities. The Review of Financial Studies, 3(4), 392-573.

Hull, J. & White, A. (1993a). One-factor interest rate models and the valuation of interest rate derivative securities. Journal of Financial and Quantitative Analysis, 28(2), 235-254.

Hull, J. & White, A. (1993b). Bond option pricing based on a model for the evolution of bond prices. Advances in Futures and Option Research, 6, 1-13.

Itô, K. (1951). On stochastic differential equations. Memoirs of American Mathematical Society, 4, 51.

Julio, J. M., Mera, S. J. & Revéiz, A. (2002). La curva spot (cero cupón): estimación con splines cúbicos suavizados, usos y ejemplos. Banco de la República. Borradores de Economía, 213.

Lamothe, P. (2003). Opciones financieras y productos estructurados (2.^a ed.). Madrid: McGraw-Hill.

Longstaff, F. & Shwartz, E. (1992). Interest rate volatility and the term structure: a two-factor general equilibrium model. The Journal of Finance, 47(4), 1259-1282.

Melo, L. F. & Vásquez, D. M. (2002). Estimación de la estructura a plazo de las tasas de interés en Colombia por medio del método de funciones B-spline cúbicas. Banco de la República. Borradores de Economía, 210.

Nelson, C. & Siegel, A. (1987). Parsimonious modeling of yield curves, Journal of Business, 70(4), 473-489.

Ramírez, F. H. (2007). Conceptos y construcción de la curva de rendimiento de TES en Colombia con las metodologías de Nelson-Siegel y Svensson. Universidad de Medellín, Colombia.

Restrepo, D. A. & Botero, J. C. (2008). Modelos unifactoriales de tipo de interés: aplicación al mercado colombiano. Universidad EAFIT, Colombia.

Tuckman, B. (2002). Fixed income securities: tools for today's market. Toronto: Wiley.

Van Deventer, D. & Imai, K. (1997). Financial risk analytics. Nueva York: McGraw-Hill Companies.

Vasicek, O. (1977). An equilibrium characterization of the term structure. Journal of  Financial Economics, 5, 177-188.

Anexos

Pruebas de estacionariedad para la serie de los rendimientos del bono TFIT15240720: como ya se mencionó en el apartado 4.1, los resultados arrojados por las pruebas evidencian que la serie de la tasa de interés en el rango de tiempo seleccionado es no estacionaria en su nivel, mientras que en su primera diferencia sí lo es.

Estimación econométrica de los parámetros velocidad de reversión, a, y tasa de largo plazo, b.

Estimación econométrica de la volatilidad σ.

Los resultados de las pruebas de autocorrelación muestran que estadísticamente no existe correlación serial de los residuos y residuos al cuadrado de los modelos seleccionados (en su primera diferencia) para órdenes menores que 10 rezagos.

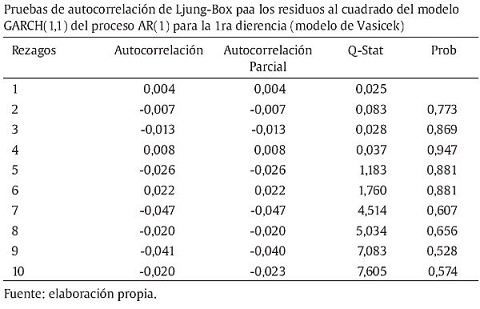
Estructura a plazo del bono con los parámetros estimados econométricamente.

La tabla A5 evidencia que la estructura a plazo del título analizado presenta un comportamiento decreciente, moderado entre los tiempos al vencimiento 1 y 2, y aún más pronunciado a partir de (T-t) mayor o igual a 2. De manera complementaria en un espacio de 10 años (específicamente de 1 a 10 años) el rango de variación de tasa de interés (_tR_T) es de 26 puntos básicos (0,26% o desde 6,88 a 7,15%).

Análisis de sensibilidad bidimensionales con los principales parámetros del modelo para el TFIT15240720.

La figura A1 evidencia que el valor de las opciones call y put es altamente sensible a la velocidad de reversión; para este caso, entre mayor sea la reversión a la media, menor es el valor de las opciones.

Figura A1. Sensibilidad de los valores de las opciones call y put vs. velocidad de reversión.

Las figuras A2 y A3 dejan ver que existe una relación directa, por un lado, entre la volatilidad de la yield y el valor de las opciones call y put; y por otro lado, entre la madurez del bono y el valor de las opciones call y put. La primera relación, además, marca un crecimiento con concavidad, mientras que la segunda exhibe crecimiento con convexidad.

Figura A2. Sensibilidad de los valores de las opciones call y put vs. volatilidad

Figura A3. Sensibilidad de los valores de las opciones call y put vs. madurez de la opción