UNA PROPUESTA METODOLÓGICA PARA LA OPTIMIZACIÓN DE PORTAFOLIOS DE INVERSIÓN Y SU APLICACIÓN AL CASO COLOMBIANO

GUILLERMO BUENAVENTURA VERA¹, ANDRÉS FELIPE CUEVAS ULLOA²

¹Profesor de tiempo completo de la Universidad Icesi; PhD (C) Nuevas Tendencias en Administración, Universidad de Salamanca; Magíster en Administración de Empresas, Eafit-Icesi; Magíster en Ingeniería Industrial y Sistemas, Universidad del Valle; Especialista en Finanzas, Universidad del Valle; Ingeniero Químico, Universidad del Valle. buenver@icesi.edu.co

²Estudiante de Décimo Semestre de Administración de Empresas, Universidad Icesi. andrescuevas@telesat.com.co

Fecha de recepción: 12-1-2005 Fecha de aceptación: 24-5-2005

ABSTRACT

The capital markets offer different alternatives for investments, where each asset have a level of given risk. The job of financial advisors is to obtain the greater yield diminishing the risk and on this subject have arisen several theories. This paper raises the development of a model and modification in Excel that allows to create efficient portfolios using Markowitz theory and also the concept of the straight line of the capital market employing assets of the real market.

KEY WORDS

International portfolio, efficient frontier, risk management, capital market line, variance, covariance, stocks, fixed income, optimization.

Rating: A

RESUMEN

El mercado de capitales constituye un universo oferente de diversas alternativas de inversión donde cada activo tiene un nivel de riesgo dado. La función de los financistas está en lograr el mayor rendimiento minimizando el riesgo y sobre este tema han surgido varias teorías. El trabajo plantea la aplicación de un modelo de optimización en Excel que permite crear portafolios eficientes a partir de la teoría del portafolio moderno de Markowitz y empleando el concepto de la línea del mercado de capitales con activos disponibles en el mercado.

PALABRAS CLAVE

Portafolios internacionales, frontera eficiente, línea de mercado de capitales, manejo del riesgo, varianza, covarianza, acciones, renta fija, optimización.

Clasificación: A

1. INTRODUCCIÓN

El trabajo desarrolla, empleando Excel, los modelos teóricos propuestos por Black (1972), Merton (1973) y más tarde por Levy y Sarnat (1982), Elton (1995) y Gruber (1997), el resumen de los cuales, expuesto por Alexander, Sharp y Bailey (2003), conduce a que el portafolio óptimo se puede encontrar utilizando principalmente la línea del mercado de capitales (LMC) y no tanto la línea de la frontera eficiente.

En la composición de portafolios eficientes se emplea la función de maximización de la rentabilidad a riesgos definidos. También, la configuración de un portafolio óptimo utilizando la línea del mercado de capitales con una función de maximización de su pendiente.

Figuran, como fuente, varios activos financieros cuyas cifras de precios históricos fueron suministradas por la compañía Suramericana de Valores (Suvalor): Acciones Colombia, Acciones Estados Unidos, Acciones Europa, Renta Fija Colombia, Renta Fija Europa y Renta Fija Estados Unidos.

La segunda parte de este artículo consigna el desarrollo del modelo y las formulaciones matemáticas correspondientes. En la tercera parte se describe la metodología en detalle y la correspondiente construcción de los modelos en Excel, mientras que en la sección cuarta se presentan la aplicación específica y los resultados del estudio.

2. DESARROLLO DE MODELOS Y FORMULACIONES

2.1 La frontera eficiente

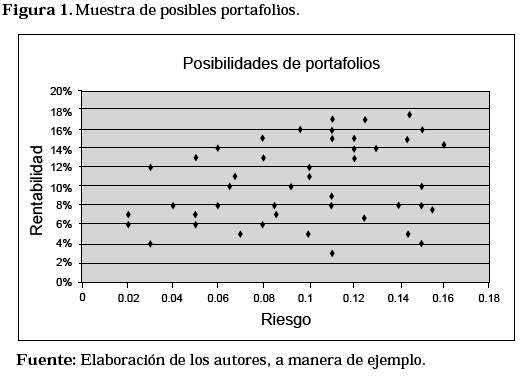
En un mercado con muchos activos el resultado final de la creación de portafolios tendrá el aspecto mostrado en la Figura 1.

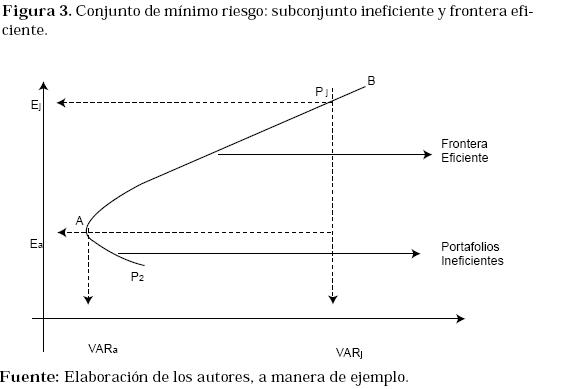
Cada punto representa un portafolio, una combinación de activos financieros. Se puede observar que algunos son mejores que otros, pues a un riesgo dado presentan mayor rentabilidad; el procedimiento a seguir entonces, es mirar cuáles son los más eficientes (es decir, mejores) dado un nivel de riesgo; la forma de establecer esta situación es la construcción de la frontera eficiente (Ver Figura 2).

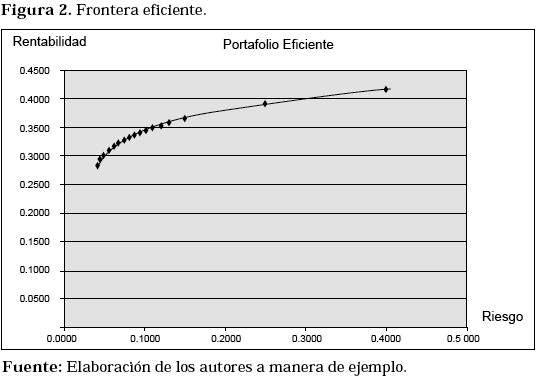
Los puntos sobre la curva en la Figura 2 representan las diferentes combinaciones de portafolios eficientes; donde se obtiene bien la mejor rentabilidad a un riesgo dado, o bien el menor riesgo a una rentabilidad dada.

Los cálculos de construcción de portafolios eficientes emplean las siguientes modelaciones:

1. Rendimiento promedio de cada activo:



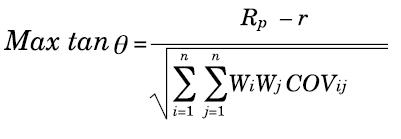
Donde Ri es el rendimiento del activo i en un período dado t y T es el número de períodos que se analizan.

2. Riesgo de cada activo, medido como la desviación típica o varianza de la rentabilidad; está dada por:



3. La covarianza entre los diferentes activos, tomados por parejas, la cual representa una medida de la tendencia de los rendimientos a moverse en la misma dirección y se obtiene mediante la ecuación:



4. La rentabilidad esperada del portafolio P se obtiene así:



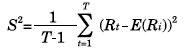
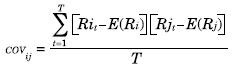
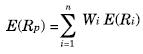
Donde Wi es el peso de cada activo en el portafolio, y n es el número de activos que participan en el portafolio.

5. El riesgo de un portafolio P con múltiples alternativas de inversión se logra mediante el cálculo de su desviación típica:



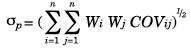
Donde σ_p es el riesgo del portafolio.

La modelación anterior da lugar a la construcción de infinidad de portafolios, de los cuales son de interés aquellos que permitan optimizar el riesgo o la rentabilidad, de manera que a cada nivel de rentabilidad se tenga el menor riesgo posible. Esta formulación se conduce de la siguiente manera:

Dado:

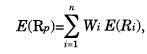
Calcular las proporciones Wi que hacen:

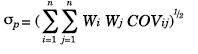
Teniendo una restricción presupuestaria:

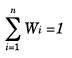
El vector solución W, cuyas n componentes son las proporciones Wi correspondientes a la fracción de la inversión del portafolio que corresponde a cada uno de los activos para conformar un portafolio cuyo rendimiento esperado es E(R_P) y cuyo riesgo global es mínimo.

Este cálculo se realiza obteniendo el producto de la inversa de la matriz de los coeficientes por el vector columna de los términos independientes. Variando E(R_p) pueden obtenerse los distintos puntos (E(R_p), σ_p) que conforman la frontera eficiente.

Es necesario determinar el punto que representa el portafolio de mínimo riesgo, pues el mismo separa el subconjunto ineficiente de la frontera eficiente que se desea construir. Matemáticamente la solución se puede dar mediante la siguiente función de Lagrange:

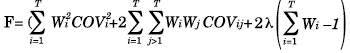
la cual se presenta en el anexo y puede seguirse en Messuti, Álvarez, Graffi (1992).

La Figura 3 muestra la curva de la frontera eficiente (AB), donde cada punto de ella representa un portafolio eficiente

2.2 La recta del mercado de capitales

Se puede obtener un solo portafolio óptimo sobre la frontera eficiente por medio del cálculo de la línea del mercado de capitales, donde el portafolio óptimo es el punto de tangencia entre la línea del mercado de capitales y la frontera eficiente. Como este portafolio óptimo está sobre la frontera eficiente, entonces el punto de tangencia debe estar localizado en la recta con máxima tangente, conformada con el punto de tasa libre de riesgo r entre y el punto de frontera eficiente.

El teorema de separación consiste en la determinación del portafolio M óptimo, lo cual requiere maximizar la pendiente de la recta:

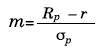
Sujeto a la restricción presupuestaria:

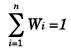
Para este cálculo se debe contar con una tasa libre de riesgo, r, o sea, la tasa de interés que posea el menor riesgo de inversión en el mercado (normalmente definida por las inversiones en títulos emitidos por el Estado).

Hay que determinar la pendiente de la recta. Gráficamente se puede expresar como aquella recta que pasa por r (tasa libre de riesgo) y tiene la máxima pendiente sin salirse de la frontera eficiente determinada anteriormente. La metodología expuesta por Vélez- Pareja (2001), es la siguiente:.

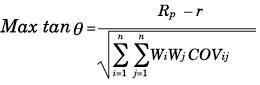
Cumpliendo:

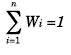
W_i es la participación de la alternativa de inversión i en el portafolio, COV_ij es la covarianza entre las parejas de títulos alternativos de inversión, r es la tasa libre de riesgo y n es el número de clases de activos que se toman para la construcción del portafolio.

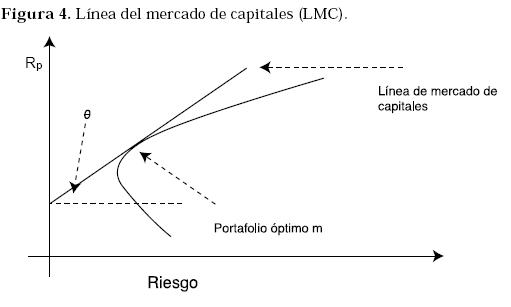
La Figura 4 muestra la línea del mercado de capitales, la frontera eficiente y el portafolio óptimo.

3. DISCUSIÓN DE LA METODOLOGÍA

3.1 Construcción de la frontera eficiente

Basado en el instrumental mostrado, se construye un modelo de configuración de portafolios óptimos utilizando el paquete de Excel propiedad de Microsoft. El modelo que se ha elaborado permite trabajar con múltiples activos. En este trabajo desarrolla una aplicación con seis activos, pero la aplicación también se puede ajustar a n activos con facilidad.

Construcción del modelo de portafolio óptimo usando Excel

1. Se debe contar con una tabla de datos históricos con los activos que se quieren analizar y sus respectivas rentabilidades a lo largo del tiempo.


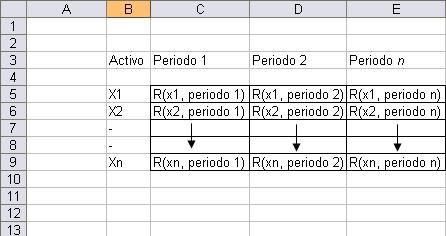
La estructura que se aprecia en la gráfica anterior muestra en la columna de B7 a B11 los diferentes activos (X₁ - X_n); la matriz conformada desde C7 hasta E11 tiene las rentabilidades de cada activo en un período determinado.

2. Se calcula la rentabilidad promedio de cada activo, la desviación típica y su varianza.

Los cálculos del promedio y desviación estándar se realizan por medio de la herramienta F_x, seleccionando la categoría estadística:


3. Se construye una tabla de correlaciones entre los diferentes activos, usando la función de Excel Covar:


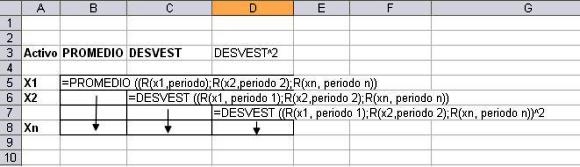
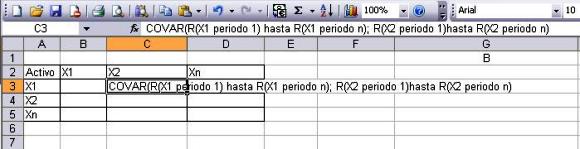
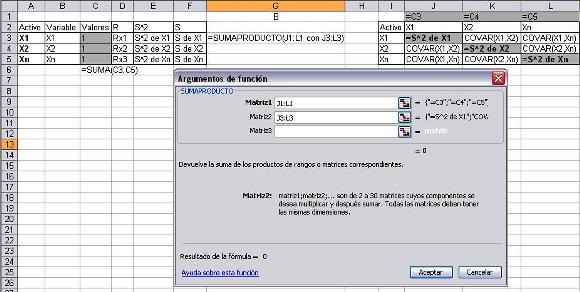
Con la función de Excel Covar se construye la siguiente matriz triangular de covarianzas:


4. Se organiza una tabla que contenga las variables mostradas en la siguiente figura de Excel, donde la columna Activo contiene los nombres de los diferentes activos y la columna Variable contiene los pesos de cada uno de los activos en el portafolio óptimo.


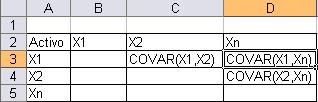
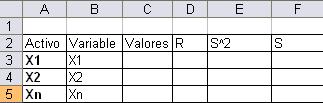
El anterior gráfico muestra las variables que debe tener la tabla que calculará las proporciones que debe tener cada activo, donde R es la rentabilidad esperada de cada activo, «Valores » es el peso de cada activo dentro del portafolio, S es desviación estándar, Sˆ2 es la varianza de cada activo y «Activo» es el valor simbólico que toma cada activo.

5. El paso siguiente es pegar la información de la tabla de covarianzas, como se muestra en el siguiente gráfico y completarla; para facilitar los cálculos posteriores se debe trabajar con la matriz completa y no con la matriz triangular.


Como se ve en la gráfica, la diagonal de la matriz de correlaciones es la varianza de cada uno de los activos.

6. Para calcular el riesgo de los diferentes portafolios se usa la fórmula general



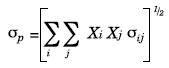
que puede ser extendida así:



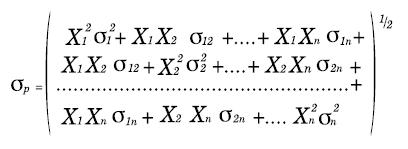
Para el caso del modelo la función Sumaproducto realizará el cálculo del riesgo.

• Se hace un Copy-paste de la rentabilidad promedio, desviación estándar y varianza de cada activo.


Se debe considerar:

a. En todo portafolio, la suma del peso de cada activo debe dar el 100%, para el modelo en las celdas que representan las rentabilidades de cada activo se le asigna el número 1 y después se suman, como se aprecia en la gráfica anterior (celda C6).

b. La celda arriba de los símbolos de cada activo debe ser igual a la de los valores de cada uno de los diferentes activos, si se mira la gráfica anterior se tiene lo siguiente: JI = C3.


• La anterior gráfica muestra la función Sumaproducto realizada en la celda G3, el resultado de la fórmula debe ser arrastrado de G3 a G5 y automáticamente saldrán los otros resultados. La matriz 1 no cambia cuando se arrastra de G3 a G5, entonces se debe usar con F4.

• La columna G muestra los resultados de la sumaproducto, después de arrastrar el resultado de G3 hasta G5.
• La celda G3 se debe multiplicar con la columna C3, el resultado se lleva a la celda G5.
• El literal A muestra la suma desde H3 hasta H5
• La fórmula de riesgo del portafolio es la raíz cuadrada de la varianza, si se tiene la varianza del portafolio en H7. El literal B muestra el riesgo del portafolio al elevar la varianza que se encuentra en H7 a la un medio.
7. Para calcular la rentabilidad del portafolio se utiliza la fórmula


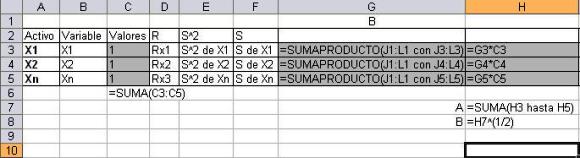
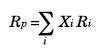
Usando la función Sumaproducto de Excel se logra calcular la fórmula de Rentabilidad esperada del portafolio.


8. El planteamiento matemático para calcular los portafolios que se encuentran sobre la frontera eficiente, en caso general es el siguiente:
• Minimizar σ_p (riesgo esperado prefijado)
• Sujeto a:
  1. E(Rp) Rendimiento esperado dado
  2. (X₁ + X₂ +... + X_n = 1 )

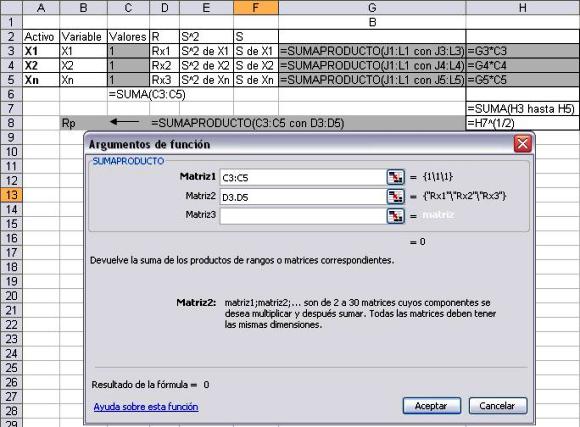
Restricción presupuestaria

Utilizando la herramienta Solver de Excel se pueden meter los parámetros anteriores para calcular la composición de los diferentes portafolios óptimos (Ver página 25).

Parámetro de Solver

a. Se usa la función Sumaproducto entre las celdas de valores y las de rentabilidades esperadas de cada activo.

b. La suma de los pesos de cada activo debe dar el 100% del portafolio. La celda C10 = 100%. Luego, en el solver, se le agrega la restricción donde la suma de los valores sea igual a 100%.

c. En la celda H12, el inversionista entra el nivel de riesgo a tolerar, para que el sistema le calcule el portafolio óptimo a ese nivel de riesgo.

d. La ventana de diálogo de Solver se configura teniendo en cuenta lo siguiente:

Celda Objeto: La celda objeto dará el resultado de la rentabilidad esperada del portafolio. (R_P)

Valor de la celda objetivo: Se selecciona Máximo.

Cambiando las celdas: Se seleccionan las celdas que se ubican en la columna de valor (Celdas que darán los diferentes pesos de cada activo).

Restricciones

• La suma de los pesos de los diferentes activos es igual a 1; dondeSuma(C3:C5) = 1, para el uso en Excel C10 = C6.
• El riesgo esperado por el inversionista es igual a la suma del riesgo de cada uno de los activos del portafolio; donde H8 es la suma del riesgo de cada uno de los activos debe ser igual a H12, riesgo esperado por el inversionista.

• Se hace click en Resolver y se obtiene la solución: el peso de cada activo dentro del portafolio con la rentabilidad esperada del mismo.
• Cada vez que se ingrese un nivel de riesgo el modelo dará una solución de portafolio que se ubica en la frontera eficiente. Se ingresa un σp para obtener un Rp. Con los datos anteriores se puede construir una tabla con diferentes σp y sus Rp obtenidos por el modelo, esto con el fin de graficar la curva de la frontera eficiente.
• En el gráfico de la parte inferior de la página se observa la tabla de los σ_p ingresados por el inversionista y su respectivo R_P, obtenidos por medio de la utilización del modelo.

• Para organizar la tabla hay que tener en cuenta que la variable X son los datos σ_p y la variable Y viene dada por los valores R_p.
• Los datos σp deben ser organizados de forma ascendente, de menor a mayor riesgo.

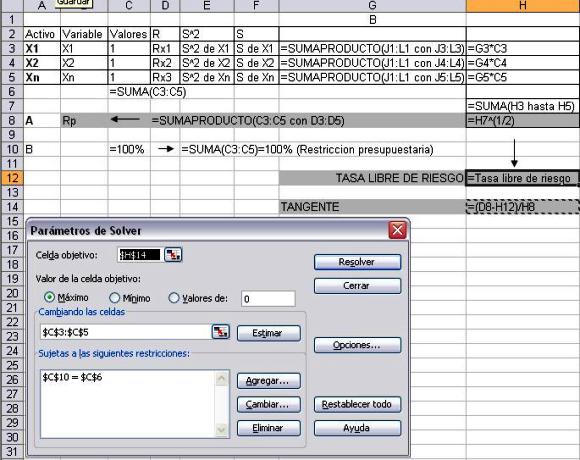
3.2 Construcción del portafolio óptimo

1. El portafolio óptimo se calcula por medio de la línea del mercado de capitales. Maximizando la recta tangente entre m y r; donde r es la tasa libre de riesgo y m es un portafolio que se ubica en la frontera eficiente, como lo propone Vélez-Pareja (2001).



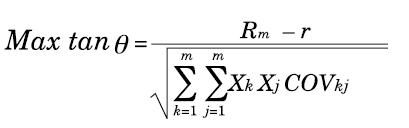
Donde: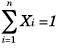

La maximización de la recta tangente entre m y r, se puede hacer usando el Solver de Excel.

• Se debe establecer la tasa libre de riesgo, r, para luego maximizar el valor

(r_P - r)/ σ_p

• Se establece una tasa libre de riesgo, celda H12.
• Se escribe la fórmula a maximizar, celda H14, donde D8 es R_P, H12 es la tasa libre de riesgo y H8 es el riesgo σ_p.
• Usando el Solver de Excel se establece la celda objetivo a maximizar, en la que tenemos la función tangente:

Celda objetivo: celda con la fórmula (R_P- Tasa libre de riesgo)/ σ_p

Restricción: La suma de los pesos de cada activo debe dar el 100% del portafolio. La celda C10 = 100%. luego en el solver se le agrega la restricción; donde la suma de los valores sea igual a 100%.

Se hace clic en Resolver y el portafolio óptimo que maximiza la recta tangente entre m y r se configura.

4. APLICACIÓN DEL MODELO

La aplicación del modelo se configura con seis tipos de activos: dos nacionales y seis internacionales, de tal manera que se tengan alternativas globales de inversión.

4.1 Base de datos

Activos que conforman el portafolio

• Renta Fija Colombia: Según DTF 90 días, calculada por el Banco de la República.
• Acciones Colombia: Según IGBC, Simulado IBB hasta diciembre de 1987, e IBOMED entre diciembre de 1987 y junio 1o. Incluye dividendos. Fuente: Bolsa de valores.
• Renta Fija Estados Unidos: Según bonos del Estado a tres meses, publicado por Bloomberg y devaluación del peso según TRM de la Superintendencia Bancaria.
• Renta Fija Europa: Según bonos BCE a tres meses, publicados en Bloomberg, y devaluación del peso según TRM de la Superintendencia Bancaria y tasa oficial del Euro (ajustada con la libra esterlina), publicada en Bloomberg.
• Acciones Europa: Según BE500 (Simulado DAX hasta diciembre de 1996), y devaluación del peso según TRM de la Superintendencia Bancaria y tasa fija del Euro (ajustada con marco alemán) publicada en Bloomberg. Incluye dividendos. Fuente: Bloomberg.
• Acciones Estados Unidos: Según S&P-500, y devaluación del peso según TRM de la Superintendencia Bancaria. Incluye Dividendos. Fuente: Bloomberg.

La base de datos provista por Suramericana de Valores (Suvalor) se encuentra en el archivo personal de los autores.¹

4.2 Cálculos

La Tabla 1 muestra la rentabilidad promedio, el nivel de riesgo de cada alternativa de inversión y la correlación entre los activos.

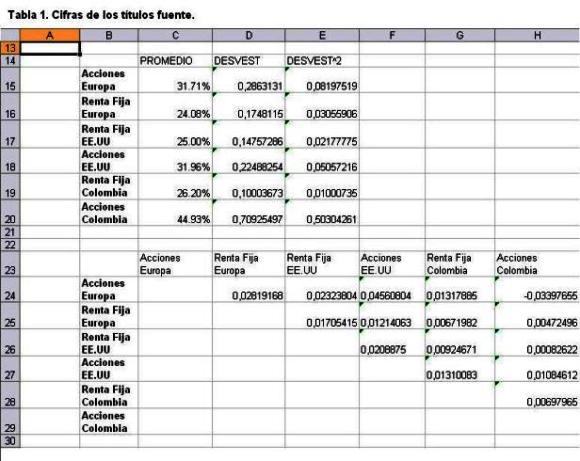
La Tabla 2 muestra el cálculo de un portafolio óptimo con un nivel de riesgo dado por el inversionista de 0.10. El modelo calcula la máxima rentabilidad posible dado un riesgo de 0.10.

La Tabla 2 muestra un portafolio con σ_P 0.10 y rentabilidad esperada de 26.65%; donde el 89% debe estar invertido en renta fija Colombia, 7% en renta fija Europa, 3% en acciones Colombia y 1% en acciones Estados Unidos.

Variando el riesgo del portafolio, Sp, se obtiene una tabla que contiene los portafolios que se ubican sobre la frontera eficiente (Tabla 3).

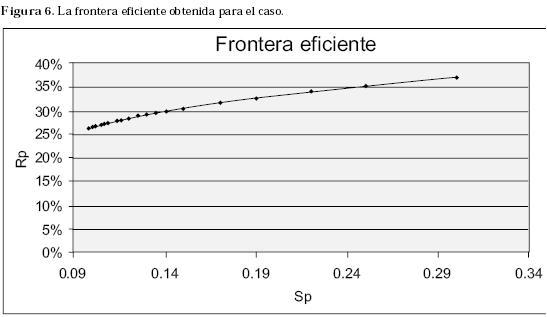
Los datos de la Tabla 3 permiten graficar la frontera eficiente; donde los Sp son la variable X y los Rp la variable Y (Figura 5).

La Figura 6 muestra la frontera eficiente, compuesta por portafolios, cuya muestra se da en la siguiente tabla:

La Tabla 4 muestra la aplicación del modelo en Excel con el objetivo de maximizar la recta tangente entre m y r; donde m es un portafolio que se ubica sobre la frontera eficiente y r es la tasa libre de riesgo.

La tasa libre de riesgo de la Figura 7 es de 13.66% y representa un promedio de la tasa de interés de los bonos del tesoro americano a diez años, para lo anterior se tomaron datos históricos desde 1991 y se tuvo en cuenta la TRM desde 1999.

5. CONCLUSIONES

La metodología expuesta en este trabajo permite construir múltiples portafolios que se ubican en la frontera eficiente por medio del análisis matemático de la evolución de las rentabilidades de los diferentes activos que lo conforman. Asimismo, y de una manera simple, se puede obtener el portafolio óptimo empleando la condición de la línea de mercado de capitales para una economía.

Toda esta modelación se logra en Excel, empleando un conocimiento intermedio de manejo de este paquete.

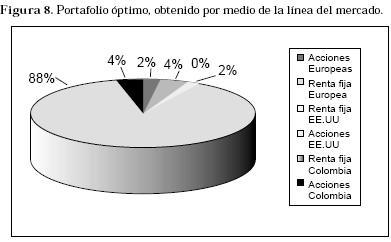
El estudio arroja un portafolio ampliamente dominado (88%) por la renta fija en moneda local. Esto se atribuye a la gran volatilidad que presentan los otros cinco componentes del mismo, al involucrar la alta variabilidad de las acciones por un lado y también la alta volatilidad de los tipos cambiarios por el otro.

El resultado obtenido para la aplicación de los seis índices de valores (Figura 8) constituye una buena guía de búsqueda de portafolios en el medio. Cabe la posibilidad de estudiar en un futuro la adecuación que los portafolios comerciales ofrecidos tienen con este hallazgo, o aun con resultados de valores originales diferentes o muy específicos.

Es imperativo advertir que en los modelos de construcción de portafolios eficientes la rentabilidad esperada, más que verse a corto plazo, se basa en proyecciones a largo plazo y está sujeta a variaciones debido al comportamiento futuro de los mercados. La probabilidad de obtener la rentabilidad esperada aumenta si se analiza la inversión con un horizonte de tiempo amplio. Este enfoque hace parte de la postura financiera práctica de proyectar el futuro con base en las variaciones del pasado, aunque en ello no se puedan prever eventos atípicos o cataclísmicos o de causa asignable no normal que puedan suceder en el futuro.

NOTAS AL PIE DE PÁGINA

1. Para su consulta se puede comunicar con los autores del artículo.

BIBLIOGRAFÍA

Gordon, Alexander. Sharpe, William & Bailey, Jeffrey. Fundamentos de inversiones, teoría y práctica, Tercera edición, México: Prentice Hall. 2003.

Eun, Ch. S. & Resnick, G. International finance management. Third edition. New York: Mc Graw Hill. 2004.

Messuti, D.J., Álvarez, V.A. & Graffi, H.R. Selección de inversiones. Buenos Aires: Ediciones Macchi. 1992.

Newbold, Paul. Estadística para los negocios y la economía. Cuarta edición. España: Prentice Hall. 1997.

Kolb, Robert W. Inversiones México: Limusa Noriega Editores. 2000.

Vélez-Pareja, J.I. «Selección del portafolio óptimo: una nota. Optimal portfolios selection». www.ssrn.com. 2001.

www.suvalor.com

www.corfinsura.com

www.Bloomberg.com

www.supervalores.gov.co