ARTÍCULOS

Superioridad relativa de los estimadores Kiviet y Blundell -Bond (GMM1) en paneles dinámicos. Un experimento Monte Carlo con muestras finitas

Relative superiority of the Kiviet and Blundell -Bond (GMM1) estimators in dynamic panels. A Monte Carlo experiment with finite samples

Superioridade relativa dos avaliadores Kiviet e Blundell-Bond (GMM1) em painéis dinâmicos. Uma experiência Monte Carlo com amostras finitas

Andrés Eduardo Rangel Jiménez

Departamento de Economía, Universidad Autónoma de Occidente, Colombia

Autor para correspondencia: Calle 11 # 43-36, Cali, Colombia. Correo electrónico: aerangel@uao.edu.co.

Historia del artículo:
Recibido el 25 de julio de 2011
Aceptado el 13 de diciembre de 2012

Resumen

Dado el amplio uso de los datos de panel en modelos dinámicos, es relevante evaluar el desempeño de sus diferentes estimadores en muestras finitas en presencia de baja y alta persistencia. El presente artículo tiene como objetivo analizar, mediante simulaciones tipo Monte Carlo, las propiedades de los estimadores de efectos fijos (LSDV), Arellano y Bond (AB -GMM1), Blundell y Bond (BB -GMM1), Anderson y Hsiao (AH) y Kiviet. Se concluye que en series no persistentes el estimador de Kiviet es el de mejor desempeño, basándose en los criterios de error cuadrático medio, sesgo y desviación estándar; con alta persistencia, el estimador BB -GMM1 es el de mejor desempeño seguido por el estimador de Kiviet, que se comporta bien excepto en micropaneles con series persistentes.

Clasificación JEL: C23, E00

Palabras Clave: Datos de panel, Modelos dinámicos, Kiviet, Método de momentos

Abstract

Given the widespread use of panel data in dynamic models, it is worth evaluating the performance of different estimators in finite samples in the presence of low and high persistence, with the latter being present in many macroeconomic series. This article analyzes the properties of the Least Square Dummy Variable (LSDV) estimators, Arellano -Bond Generalized Method of Moments Stage 1 (AB -GMM1), BBGMM1 (), AH (Anderson -Hsiao), and Kiviet using a Monte Carlo experiment. The results show that, in the presence of low persistence, the Kiviet estimator is the best performer based on the criteria of Root -Mean -Square Error (RMSE), bias and standard deviation. Meanwhile in the case of high persistence, the system estimator of Blundell and Bond (GMM1) is the best performing estimator against their rivals, followed by Kiviet estimator that exhibits good behavior, except in micropanels.

JEL clasification: C23, E00

Keywords: Panel data, Dynamic models, Kiviet, Generalized method of moments

Resumo

Devido à ampla utilização dos dados do painel em modelos dinâmicos, é relevante avaliar o desempenho dos seus diferentes avaliadores em amostras finitas na presença de baixa e alta persistência. O presente artigo tem como objectivo analisar, através de simulações tipo Monte Carlo, as propriedades dos avaliadores de Efeitos Fixos (LSDV), Arrellano e Bond (AB-GMM1), Blundell e Bond (BB-GMM1), Anderson e Hsiao (AH) e Kiviet. Conclui-se que em séries não persistentes o avaliador de Kiviet é o de melhor desempenho baseando-se nos critérios de erro quadrático médio, obliquidade e desvio padrão; com alta persistência o avaliador BB-GMM1 e o melhor desempenho seguido pelo avaliador de Kiviet que se comporta bem excepto em micro-painéis com séries persistentes.

Classificação JEL: C23, E00

Palavras-chave: Dados de Painel Modelos dinâmicos Kiviet Método de momentos

1. Introducción

La aplicación de datos de panel dinámicos a diversos campos de la economía ha ganado terreno en los últimos años. Al respecto anota Bond (2002): ''La ventaja de la aplicación de datos de panel para la estimación de modelos econométricos dinámicos es contundente, dado que no es posible estimar tal tipo de modelos a partir de observaciones en un solo punto del tiempo, siendo inusual que las encuestas de corte transversal proporcionen suficiente información sobre periodos de tiempo anteriores con el fin de estudiar relaciones dinámicas''.

El uso de datos de panel dentro de la macroeconomía es particularmente apropiado al estimar relaciones comunes a través de los países, permitiendo la identificación de efectos específicos a los países, controlando por variables no observadas.

Estudios sobre la relación salarios y desempleo, cuyo trabajo pionero desarrollado por Blanchflower y Oswald (1994) denominado ''curva de salarios'', da origen a numerosas aplicaciones, como lo son modelos dinámicos de determinación de salarios nominales.

Muchos conjuntos de datos macroeconómicos de panel tienen una dimensión temporal grande y una dimensión transversal mucho más pequeña que el típico panel microeconómico. Esta diferencia es particularmente importante en la elección de una técnica de estimación; de esta forma, la técnica de efectos fijos que usa variables ficticias para estimar los efectos individuales arroja estimaciones sesgadas cuando la dimensión temporal del panel (T) es pequeña. Por lo tanto, muchos macroeconomistas se plantean la pregunta: ''¿Cuán grande debería ser T para que el sesgo sea ignorado?'' (Judson y Owen, 1999).

Dada la práctica cada vez más común de este tipo de modelos, se pone de relieve la importancia de evaluar el desempeño de los paneles dinámicos en muestras finitas. El presente artículo continúa la línea de los trabajos de Arellano y Bond (1991) y Bond (2002) al analizar las propiedades de los diferentes estimadores tales como LSDV, AB-GMM1 (Arellano-Bond), BB-GMM1 (Blundell-Bond), AH (Anderson-Hsiao) y Kiviet en paneles dinámicos.

El objetivo del presente artículo es recrear mediante un experimento Monte Carlo, un modelo datos de panel dinámico y evaluar el desempeño de los diferentes estimadores en términos de sesgo, consistencia y eficiencia al variar N (observaciones de corte transversal) y T (observaciones de corte temporal). La riqueza del ejercicio consiste en recrear micro y macropaneles, los primeros comunes en el estudio de productividad de las firmas en las cuales la dimensión temporal no es muy grande, y los segundos con características normalmente encontradas por macroeconomistas. Asimismo, y dado que muchas de las series macroeconómicas presentan persistencia, se evalúa adicionalmente el desempeño de los diversos estimadores en presencia de baja y alta persistencia.

El artículo se desarrolla en dos grandes secciones. En la primera se presenta una síntesis de los diversos estimadores, seguida de la especificación del modelo recreado en el experimento Monte Carlo. Una segunda sección la constituye la evaluación del desempeño de los diversos estimadores en términos de sus propiedades cuando se modifican los parámetros del modelo dinámico y las dimensiones de N y T. Finalmente, se encuentran las conclusiones.

2. Una síntesis de los estimadores

2.1 El estimador LSDV (Least Squares Dummy Variable Model)

En este tipo de modelo mientras las pendientes están constantes, los interceptos, que son específicos a las unidades de corte transversal (eje: firmas), pueden variar, dejando de lado los efectos temporales. Este modelo es una opción comúnmente utilizada por los macroeconomistas en relación con el modelo de efectos aleatorios, básicamente por dos razones. La primera reside en que si el efecto individual representa variables omitidas, es altamente probable que estas características específicas estén correlacionadas con otros regresores. La segunda razón es que, por ejemplo, en estudios que analizan relaciones a través de los países, una base de datos de panel estándar contendrá la mayor parte de las observaciones de interés, lo que le resta el carácter de muestra aleatoria (Judson y Owen, 1999).

El modelo dinámico a estimar es el siguiente:

El término de error del modelo (v_it) está compuesto por un efecto específico individual c_i no observable e invariante en el tiempo, el cual permite capturar heterogeneidad en la media de las series de la variable dependiente (y_it) a través de los individuos, y un término de perturbación u_it. En este caso, hay dos fuentes de persistencia c_i y y_i,t-1.

Como lo anota Bond (2002), dado que los estimadores de efectos fijos solo dependen de las desviaciones respecto a las medias de sus grupos, también toman la referencia de estimadores intragrupos (Within-Groups Estimators).

Eliminando la fuente de la inconsistencia presente en el modelo en niveles, la transformación de la ecuación mediante primeras diferencias elimina el efecto individual no observable. Sobre este modelo en diferencias se aplica MCO para obtener los estimadores de interés:

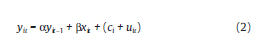
Ubicando el modelo en desviaciones respecto a los promedios del individuo:

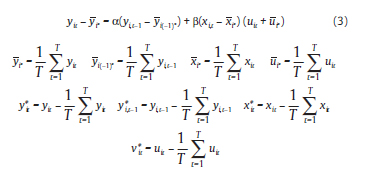
Recordando la especificación del estimador 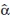¹:

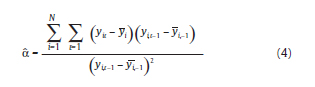
En este caso y*_i,t-1 y v*_it están correlacionados dado que ambos dependen de u_i,t-1, teniendo que el estimador es sesgado e inconsistente (Hsiao, 2003). Se recuerda que al eliminar el efecto individual se genera una correlación entre la variable dependiente rezagada transformada y el término de error, correlación que viene dada por la esperanza del numerador de la expresión (5):

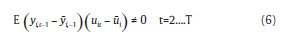
Nickell (1981) comprueba que:

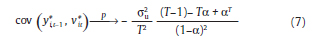
Lo cual se cumple cuando N→ ∞ para un T fijo (pequeño), siendo entonces el estimador de Efectos Fijos inconsistente. No obstante lo anterior, si T → ∞, cov De manera que la inconsistencia del estimador de Efectos Fijos se relaciona fundamentalmente cuando T es pequeño y, por lo tanto, el estimador LSDV tiene un buen comportamiento solo cuando la dimensión temporal del panel es grande.

Al violarse el supuesto de exogeneidad estricta y estimar el modelo (1) por MCO o por LSDV, el estim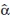ador pierde la propiedad de consistencia. El ejercicio Monte Carlo comprueba que el estimador 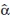es consistente con T; sin embargo, el sesgo no desaparece cuando N tiende a infinito². Esto es de particular importancia dado que es común encontrar micropaneles en los cuales se tiene una gran cantidad de información transversal (N) y pocas observaciones temporales (T).

2.2 El estimador de Anderson-Hsiao

Una transformación que elimina el efecto individual c_i consiste en tomar diferencias en (1):

En este caso, MCO es inconsistente dado que Δu_it y Δ yi,t-1 están correlacionados al depender ambos de u_i,t-1. No obstante y_i,t-2 y Δy_i,t-2 = y_i,t-2 - yi,t-2, aunque correlacionadas con Δy_i,t-1, pues ambas dependen de y_i,t-2, no estas con Δu_it. Luego Δy_i,t-2 y y_i,t-2 constituyen instrumentos válidos para la obtención de estimadores cuando N o T tienden a infinito.

El estimador de Anderson-Hsiao puede ser considerado como un caso especial de los procedimientos del estimador de método generalizado de momentos (GMM) al usar todos los valores rezagados de la variable dependiente además de los rezagos de las variables exógenas como instrumentos. Se debe destacar que cuando las variables explicativas x_it son predeterminadas pero no estrictamente exógenas, solo los valores rezagados de las variables explicativas son instrumentos válidos.

Los estimadores de variables instrumentales se especifican a continuación (Anderson y Hsiao, 1982):

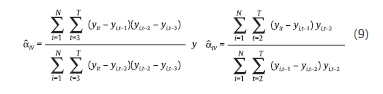
2.3. El estimador de Arellano y Bond

Arellano y Bond (1991) toman diferencias en (1) y, eliminando el término individual, llegan al siguiente modelo:

El primer periodo donde se observa esta relación es en t=3.

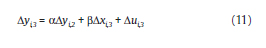
En este caso, y_i,1 es un instrumento válido al estar correlacionado con Δy_i,2 pero no correlacionado con Δu_i,3. Para el siguiente periodo t=4, la relación es:

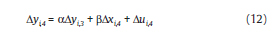
En este caso, los instrumentos validos son y_{i,2 y} y_i,1. Siguiendo la lógica, los instrumentos disponibles para T son y_i,1, y_i,2,..., yi,T-2. En general, esta lógica implica las siguientes 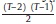condiciones de momentos.

Para la estimación mediante el GMM, las condiciones son las siguientes:

donde Z_i es una matriz de instrumentos, cuya forma es:

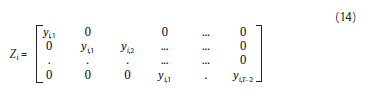
El estimador generalizado de momentos minimiza:

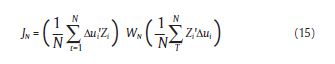
Para obtener el estimador α_GMM1, en un paso bajo el supuesto de que los errores son homocedásticos, se utiliza la siguiente matriz de ponderaciones:

donde H es una matriz cuadrada de dimensión T-2, con 2's en la diagonal principal y -1's en una de las primeras subdiagonales y ceros en otro caso.

Existe otro tipo de estimador, 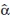_GMM2 (estimador GMM de dos pasos), obtenido a partir de una matriz de ponderaciones en la cual

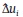
corresponde a estimaciones consistentes de los residuos en primeras diferencias. Estas estimaciones son obtenidas a partir de un estimador preliminar consistente como lo es α_GMM1 (Bond, 2002). La especificación en este caso es:

Se debe anotar que el estimador de GMM de Arellano y Bond (1991) para un modelo en primeras diferencias es más eficiente que el estimador de Anderson y Hsiao (1982) al utilizar un número más grande de instrumentos en la estimación (véase matriz Z_i), lo cual es confirmado por el experimento Monte Carlo.

2.4. El estimador de Blundell y Bond

El estimador de sistemas GMM de Blundell y Bond sugiere las primeras diferencias como instrumentos para la ecuación en niveles e instrumentos en niveles para la ecuación en primeras diferencias (Bruno, 2004). El estimador se basa en la combinación de ecuaciones en diferencias con ecuaciones en niveles y las siguientes condiciones de momentos:

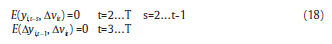
Tomando como instrumentos de las primeras diferencias a los rezagos de las variables, estos se tornan débiles si el parámetro α es cercano a la unidad. La consecuencia inmediata es que los estimadores basados en variables instrumentales pierdan la propiedad de insesgamiento en presencia de instrumentos débiles. La naturaleza del sesgo en muestras finitas del estimador GMM1 de Arellano y Bond es hacia abajo, característica que comparte con el estimador LSDV.

En contraste el estimador de Blundell y Bond, exhibe no solo un sesgo menor, sino una mayor precisión en relación con los estimadores alternativos (véase experimento Monte Carlo).

2.5. El estimador Kiviet

El estimador Kiviet (1995) surge como respuesta a la inconsistencia del estimador Least Square Dummy Variable (LSDV) en muestras finitas cuando se trabajan con paneles dinámicos. Kiviet parte del estimador LSDV, del cual logra remover el sesgo usando estimadores GMM consistentes de 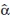. Siguiendo a Bruno (2004), el estimador de Kiviet (LSDVC) que corresponde al estimador LSDV después de remover el sesgo queda expresado como:

La estimación de la corrección del estimador LSDV también involucra un procedimiento de dos pasos, en el cual los residuales del estimador consistente (el cual puede ser el de Anderson-Hsiao) son usados para calcular el sesgo en un segundo paso. Para más detalles del cálculo del sesgo, véase Judson y Owen (1999).

3. Simulación Monte Carlo

En esta sección se describe el ejercicio tipo Monte Carlo que se usó para investigar las propiedades relevantes de los diferentes estimadores que los macroeconomistas desean evaluar. Como criterio de evaluación de los diferentes estimadores, se utiliza el error estándar, el RMSE y la media para evaluar el sesgo. Respecto a esta última, se procede a calcular el promedio de los estimadores a través de todas las simulaciones:

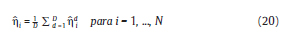
donde D el número de simulaciones y η^d_i es el correspondiente estimador para la unidad i de la simulación d. Por otro lado, la raíz media del error al cuadrado (RMSE) se define como:

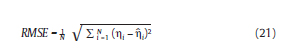
La razón para escoger esta medida es, que además de reflejar el sesgo, refleja la dispersión de los estimadores.

El proceso generador de datos en esta simulación esta dado por el siguiente modelo autorregresivo:

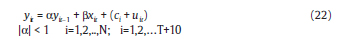
Este ejercicio sigue la misma línea de Arellano y Bond (1991), Kiviet (1995) y Bun y Kiviet (2003) al especificar solo un regresor que acompaña a la variable endógena rezagada. La variable explicativa x_it cumple con el supuesto de exogeneidad estricta, cuyo proceso generador de datos es:

Un supuesto clave es que los términos de error u_it son independientes a través de los individuos siguiendo una distribución normal estándar:

Los efectos individuales se asumen estocásticos y, por tanto, correlacionados con la variable dependiente rezagada, esto es:

Solo en el caso de que el término c_i tuviera una distribución degenerada, esta esperanza sería igual a cero, excepción que en este caso no se cumple pues se especifica que el efecto fijo varió entre los individuos siguiendo una distribución normal, con media cero y varianza 1:

Lo que va en la vía de lo hecho por Arellano y Bond (1991), donde:

Dados estos supuestos, estimar el modelo (1) por MCO en niveles arroja estimaciones inconsistentes de α, toda vez que la variable y_i,t-1 esté correlacionada con el término de error, dada la presencia de un efecto individual no observable:

Para finalizar la especificación del modelo se establece como condición inicial y_i0 = 0. La razón para hacerlo radica en la influencia de las observaciones iniciales en las subsecuentes observaciones, detalle que no es seguro ignorar cuando se trabajan con micro paneles en los cuales se tienen pocas observaciones sobre T (Bond, 2002). Se descartan entonces las primeras 10 observaciones, de manera que los resultados del experimento no dependan de esta condición inicial, siendo el tamaño muestral de NT.

Se realiza un experimento de Monte Carlo con 1.000 simulaciones con diferentes dimensiones de N y T con el fin de evaluar el desempeño de los estimadores cuando se trabajan con micro y macropaneles. Seguidamente, se recrea baja y alta persistencia al variar el coeficiente que acompaña a la variable dependiente rezagada.

3.1. Desempeño de los estimadores cuando T es fijo y N tiende a infinito

La tabla 1 resume los resultados del experimento inicial para un subconjunto de valores paramétricos σ ²_c normalizado a 1, y α con un valor intermedio de 0,5. Se presentan los resultados de los 5 estimadores cuando el tamaño del panel cambia en su dimensión transversal tomando valores de 30 y 50, y manteniendo la dimensión temporal T fija en 10.

En la primera simulación tipo Monte Carlo (véase la tabla 1), se encuentra que el estimador de Anderson y Hsiao, con un promedio de 0,5074, es el de menor sesgo. No obstante, si se toma como parámetro el menor RMSE, el mejor estimador resulta el de Kiviet, siendo su RMSE un 50% menor que el de Anderson y Hsiao. Teniendo en cuenta que el sesgo del estimador de Kiviet no es muy grande y con un RMSE menor a todos los estimadores, se concluye que Kiviet es el mejor estimador (lo cual se logra al remover el sesgo presente en los estimadores LSDV). Para este ejercicio de Monte Carlo también la evidencia muestra que los estimadores de Kiviet superan lo hecho por el estimador GMM de Blundell-Bond en términos de sesgo (promedio de Kiviet es 0,4173 contra 0,6967 de Blundell y Bond) y de la raíz del error medio cuadrático, RMSE (0,011 y 0,046, respectivamente).

Al aumentar el tamaño de N, el RMSE de todos los estimadores disminuye significativamente, así como su desviación estándar, excepto para el estimador LSDV. La otra regularidad que se observa es que el sesgo entendido como la diferencia entre el parámetro poblacional y el promedio, disminuye para todos los estimadores, excepto de nuevo para el estimador LSDV el cual no es consistente con un T fijo y con un N tendiendo a infinito. Finalmente, se confirman las ventajas de los estimadores GMM de Arellano y Bond en paneles dinámicos cuando T es fijo (pequeño) y N → ∞.

3.2. Desempeño de los estimadores cuando N es fijo y T aumenta

A continuación, en la tabla 2, se analizan las propiedades de los diversos estimadores aumentando la dimensión temporal (T) y fijando la dimensión transversal (N) en 50.

En la tabla 1, al aumentar el tamaño de la muestra (N pasa de 30 a 50), se evidencia que el estimador LSDV para modelos autorregresivos no es consistente para muestras pequeñas, con un sesgo que está asociado al tamaño de la dimensión temporal (T). Entre tanto, en la segunda simulación Monte Carlo (véase la tabla 2), al pasar de un T = 10 a T = 30 el estimador LSDV se acerca bastante al parámetro poblacional.

La anterior regularidad confirma que, en general, al aumentar la dimensión temporal, los estimadores LSDV (Within) son consistentes, lo cual es contrario a lo sucedido con los estimadores GMM. En este caso se puede observar que el procedimiento de un paso GMM1 (Arellano y Bond 1) mejora lo hecho por el estimador de sistemas de Blundell y Bond, en términos de producir un sesgo menor y una menor desviación estándar cuando se incrementa la dimensión temporal. Kiviet, con el menor sesgo y RMSE, resulta ser el mejor estimador en términos relativos.

Se debe destacar que, en la actualidad, existen programas que permiten la extracción del estimador de efectos fijos (LSDV) del estimador de Kiviet (LSDVC). Un ejemplo de ello es STATA, cuyo respectivo comando es xtlsdvc³.

3.3. Desempeño de los estimadores cuando en presencia de series persistentes

En la tabla 3 se recrea un macropanel con 20 observaciones en la dimensión temporal y 30 en la dimensión transversal, evaluando el desempeño de los diversos estimadores cuando el coeficiente autorregresivo pasa de 0,5 a 0,8, dada la alta persistencia presente en la mayoría de la series macroeconómicas.

Simulando un macropanel con un coeficiente α de 0,8, el estimador de Kiviet es preferible al tener un menor RMSE que sus competidores, con un sesgo relativamente menor. Por otro lado, el estimador de Arellano y Bond supera lo hecho por Anderson-Hsiao en términos del RMSE y desviación estándar, lo cual confirma la superioridad de estas estimaciones IV (variables instrumentales) por GMM respecto a las demás cuando el coeficiente α se acerca a 1.

Como se recordaba en la síntesis inicial, Blundell y Bond (2000) anotan que los estimadores pueden sufrir de un sesgo debido a la presencia de instrumentos débiles (lo cual ocurre cuando el parámetro α pasa de 0,8 a 0,92). Como solución, estos autores sugieren un estimador del sistema GMM agregando un solo instrumento por periodo temporal a las ecuaciones en niveles. La simulación confirma que en presencia de instrumentos débiles bajo alta persistencia (α = 0,92), el estimador de Blundell y Bond es relativamente más eficiente con un RMSE de 0,0081 y con una desviación estándar de 0,0043 en comparación con un RMSE de 0,0264 y una desviación estándar de 0,0158 (con un α = 0,80), Por su parte, el estimador de Kiviet compite con el estimador de Blundell-Bond porque presenta un menor sesgo, con 0,0369 frente a 0,0764 al aumentar la persistencia del proceso, lo cual se complementa con una relativa eficiencia.

3.4. Desempeño de los estimadores en presencia de series persistentes con micropaneles

A continuación, en la tabla 4, se evalúan las propiedades de los estimadores en presencia de alta persistencia, esta vez pasando de la simulación de un macropanel a un micropanel. Se confirma, entre otros resultados, la consistencia del estimador LSDV en relación con la dimensión T.

En efecto, con un periodo T pequeño se observa un mayor sesgo del estimador LSDV, incluso en presencia de alta persistencia. El estimador de Kiviet con un RMSE de 0,0047, una desviación de 0,0406 le sigue en desempeño al estimador de sistemas GMM, evidenciando de nuevo como el de mejor desempeño promedio en todos los ejercicios de simulación.

Otro escenario se configura al aumentar la persistencia de la variable dependiente (al pasar a un α de 0,92). En esta simulación, el estimador de Blundell y Bond resulta ser el mejor con el mejor RMSE (0,0181) y una desviación estándar de 0,1040, lo cual evidencia su superioridad frente a los demás estimadores en presencia de instrumentos débiles. A diferencia del caso anterior de alta persistencia en macropaneles, en este escenario de micropanel (con un α = 0,92), el estimador de Kiviet muestra un pobre desempeño en términos de sesgo y eficiencia.

4. Conclusiones

Es de suma importancia conocer las propiedades de los diferentes estimadores en el momento de estimar paneles dinámicos, toda vez que las propiedades de insesgadez, consistencia y eficiencia no solo dependen de las dimensiones N y T, sino también de algunos otros parámetros, como es el caso del coeficiente que acompaña a la variable endógena rezagada (α).

La recomendación antes de elegir el estimador dependerá de la relación existente entre la dimensión transversal (N) y temporal (T). Por ejemplo, la propiedad de consistencia del estimador LSDV se cumple con un T grande y N pequeño, mientras que en los estimadores GMM esta propiedad se alcanza con un N grande y T pequeño. Dado este resultado, los macroeconomistas no deberían desestimar el sesgo del estimador LSDV con una dimensión temporal pequeña y una gran dimensión transversal.

Se debe señalar que el estimador GMM1 de Arellano y Bond con series no persistentes (coeficiente α < 0,5) tiene un buen desempeño; no obstante, es superado por el LSDV corregido (Kiviet) en términos de las propiedades de insesgadez y eficiencia.

La anterior situación se revierte en un micropanel con un N grande y T pequeño, donde el sesgo de los estimadores GMM1 de Arellano y Bond se vuelve considerable cuando las series son altamente persistentes. Por lo tanto, se recomienda cuando se vayan a estimar paneles dinámicos con estimadores GMM, indagar si las series tienen alta persistencia y si este es el caso utilizar los estimadores de sistemas GMM de Blundell y Bond.

El estimador de Kiviet resulta ser el mejor estimador con series no persistentes frente a los demás estimadores al exhibir un menor RMSE, desviación estándar y sesgo. No obstante en series altamente persistentes no muestra un buen desempeño según los criterios mencionados, estando por debajo de los estimadores GMM1 de Blundell y Bond quienes muestran un mejor desempeño en presencia de alta persistencia.

Agradecimientos

Se agradece al director de la Maestría en Econometría y profesor del curso Datos de Panel, Martin Gonzalez Rozada, por los conocimientos adquiridos durante el curso. Este artículo se basa en uno de los trabajos aplicados entregados en clase durante el desarrollo del curso Datos de Panel. A Pablo Grigoriu, mi gratitud por su colaboración para la construcción del código de Matlab que recrea los resultados.

NOTAS

1. Dado que el término de error especificado sigue una distribución normal estándar, el estimador (4) también constituye un estimador máximo verosímil (Hsiao, 2003).

2. La simulación confirma los hallazgos en otros estudios al encontrar un sesgo hacia abajo del estimador LSDV.

3. Se debe destacar que, en la actualidad, existen programas que permiten la extracción del estimador de efectos fijos (LSDV) del estimador de Kiviet (LSDVC). Un ejemplo de ello es STATA cuyo respectivo comando es xtlsdvc.

Bibliografía

Anderson, T. W., & Hsiao, C. (1982). Formulation and estimation of dynamic models using panel data. Journal of Econometrics 18, 243-261.

Arellano, M., & Bond, S. (1991). Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. Review of Economic Studies, 58, 277-297.

Blanchflower, D., & Oswald, A. (1994). Estimating a wage curve for Britain: 1973-90. Economic Journal Royal Economic Society, 104, 1025-1043.

Blundell, R. W., & Bond, S. (2000). GMM Estimation with persistent panel data: an application to production functions. Econometric Reviews, 19, 321-340.

Bond, S. (2002). Dynamic panel data models: a guide to micro data methods and practice (The Institute for Fiscal Studies Department of Economics, UCL Cemmap Working Paper CWP09/02). Disponible: http://www.cemmap.ac.uk/wps/cwp0209.pdf

Bruno, G. (2004). Estimation, inference and Monte Carlo analysis in dynamic panel data models with a small number of individuals. Universitá Bocconi. Istituto di Economia Politica. Disponible en: http://www.stata.com/meeting/1italian/bruno.pdf

Bun, M., & Kiviet, J. (2003). On the diminishing returns of higher-order terms in asymptotic expansions of bias. Economics Letters, 79, 145-152.

Hsiao, C. (2003). Analysis of panel data (2. ed.). Cambridge: University Press.

Judson, R., & Owen, A. (1999). Estimating dynamic panel data models: a guide for macroeconomists. Economics Letters, 65, 9-15.

Kiviet, J.F. (1995). On Bias, inconsistency and efficiency of various estimators in dynamic panel data models. Journal of Econometrics, 68, 53-78.

Nickell, S. J. (1981). Biases in dynamic models with fixed effects. Econometrica, 49, 1417-1426.