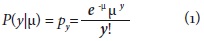
ARTÍCULOS

Ambiente regional y desempeño innovador de las firmas. Una propuesta de análisis multinivel

Regional environment and innovative company performance. A proposal for a multilvel analytical approach

Ambiente regional e desempenho inovador das empresas. Uma proposta de análise multinível

JULIO CÉSAR ZULUAGA JIMÉNEZ, Ph.D. (c)¹; IVÁN DARÍO SÁNCHEZ MANCHOLA, MSc., Ph.D.² (c); FERNANDO BARRIOS AGUIRRE, Mg³.

1 Profesor Asistente, Pontificia Universidad Javeriana Bogotá, Colombia. ivansanchez@javeriana.edu.co.

Este documento fue seleccionado en la convocatoria para enviar artículos, Call for Papers, realizada en el marco del ''II Simposio Iberoamericano de Estudios Gerenciales: Una mirada interdisciplinar a la innovación'', organizado por la revista académica Estudios Gerenciales bajo la dirección de la Facultad de Ciencias Administrativas y Económicas de la Universidad Icesi; el evento tuvo lugar los días 12, 13 y 14 de octubre de 2011, en la ciudad de Cali (Colombia). Este documento fue presentado en las sesiones simultáneas del área de ''Innovación en modelos y análisis económicos''.

Autor para correspondencia. Dirigir a: Universidad de los Andes. Edificio Aulas AU, La Liga. Of. 202. Bogotá, Colombia.

2 Profesor Asistente, Pontificia Universidad Javeriana Bogotá, Colombia. ivansanchez@javeriana.edu.co

3 Profesor Asociado, Universidad Jorge Tadeo Lozano, Colombia. fernando.barrios@utadeo.edu.co.

Recibido: 30-jun-11, corregido: 27-abr-12 y aceptado: 26-jun-12

Clasificación JEL: O31; O32

RESUMEN

El objetivo del artículo es proponer un modelo de análisis multinivel de la innovación. Se exponen los debates acerca de los efectos del ambiente regional sobre el desempeño innovador de las firmas y se sostiene que la innovación se debe comprender desde una óptica multinivel que incluyan las características del ambiente regional así como las capacidades de la firma. Para lograr este objetivo, se construyó un modelo estadístico multinivel, el cual arrojó evidencia sobre los beneficios de este enfoque en la innovación empresarial. Los resultados sugieren el enfoque multinivel para futuras investigación sobre innovación.

Palabras clave. Contexto regional; modelos multinivel; innovación empresarial.

ABSTRACT

The purpose of this article is to propose a model for a multilevel analysis of innovation. It presents different points of view about the effects of the regional environment on the innovative performance of firms, and states that innovation can only be properly understood from a multilevel perspective that considers the characteristics of the regional environment and the company capabilities. To accomplish this purpose, a multilevel statistical model was built which yielded evidence of the benefits of a multilevel approach to business innovation. The findings suggest a multilevel approach that can be used for further research on the topic of innovation.

Keywords. Regional environment; multilevel models; business innovation.

RESUMO

O objetivo deste artigo é propor um modelo de análise multinível da inovação. São apresentados os debates acerca dos efeitos do ambiente regional sobre o desempenho inovador das empresas e se defende que a inovação deve ser entendida a partir de uma perspectiva multinível, que inclua as características do ambiente regional bem como as capacidades da empresa. Para alcançar este objetivo, foi construído um modelo estatístico multinível, o qual evidenciou os benefícios da abordagem multinível na inovação empresarial. Os resultados sugerem a abordagem multinível para futuras pesquisas sobre inovação.

Palavras-chave. Contexto regional; modelos multinível; inovação empresarial.

Introducción

Los procesos de innovación no toman lugar en el vacío. Toda innovación es, al menos, un fenómeno de dos niveles que involucra primero un actor (un individuo, un equipo, una unidad, una organización) y segundo un amplio ambiente dentro del cual el actor se encuentra inmerso (Gupta, Tesluk & Taylor, 2007). Los efectos de un nivel sobre otro son mutuamente dependientes.

A su vez, como muchas teorías organizacionales enfatizan desde la perspectiva de sistemas abiertos (Scott, 2003), las organizaciones son entidades que se encuentran en una relación de interdependencia con el ambiente. Las contingencias del ambiente ejercen una influencia sobre la estructura de las firmas (Lawrence & Lorsch, 1967) y el ambiente institucional determina la forma en que las organizaciones responden ante las incertidumbres (DiMaggio & Powel, 1991).

Sin embargo, la mayoría de las investigaciones sobre innovación han tendido a centrarse en sólo un nivel de análisis (el individuo, los equipos, las firmas, los clústeres de firmas, etc.), siendo escasas las investigaciones que abordan y combinan explícitamente diferentes niveles de análisis³.

En los estudios sobre procesos de innovación poco se sabe acerca de cómo las variables en un nivel de análisis influencian la innovación en otro nivel, cómo variables en los diferentes niveles de análisis interactúan en determinar la extensión y el tipo de resultados de innovación y cómo los procesos y/o mecanismos de innovación, pueden ser aplicados a diferentes niveles de análisis y el grado en que los constructos y procesos que son parte de la innovación a múltiples niveles de análisis comparten similares antecedentes y consecuencias (Gupta et al., 2007).

El objetivo de este artículo es llenar parte de este vacío en las investigaciones sobre la innovación, desarrollando una perspectiva de análisis multinivel. Mediante la discusión del enfoque multinivel, se propone un modelo de análisis que tiene en cuenta los efectos de las variables de nivel firma y variables de ambiente regional sobre el desempeño innovador de las firmas colombianas.

El artículo se estructura de la siguiente manera, luego de esta introducción. En la segunda parte se aborda la perspectiva de análisis multinivel y su relación con el estudio de la innovación y se presenta la revisión de la literatura sobre la relación entre ambiente regional e innovación de las firmas. En la tercera parte se presenta el modelo econométrico propuesto, la metodología, los datos y medidas empleadas en la investigación. En la cuarta parte se presentan los resultados, conclusiones y posibles líneas de investigación desde la perspectiva multinivel.

1 Revisión de la literatura y formulación de hipótesis

1.1 Teoría multinivel

La teoría multinivel permite comprender cómo los fenómenos y procesos de un nivel de análisis están relacionados/anidados con los de otro nivel (Klein, Dansereau & Hall, 1994; Rousseau, 1985) y proporciona una perspectiva más rica, completa y compleja de determinados fenómenos como la innovación. Igualmente, la innovación puede ser analizada en y a través de diferentes niveles como el individual, grupos/equipos, industrial y regiones geográficas.

Existen dos tipos de enfoques multinivel. El primero, el bottom-up emergent processes (procesos emergentes de abajo hacia arriba) y el segundo, el top-down processes o contextual influences. Aunque una perspectiva multinivel completa requiere de la inclusión de ambas perspectivas (Gupta et al., 2007), y la consideración de los diferentes niveles de análisis involucrados en los procesos de innovación, en este estudio sólo se discute la top-down,⁴ por considerarla fundamental para explicar y comprender la influencia de variables ambientales sobre el desempeño innovador de las firmas y los diferenciales en desempeño innovador de las regiones. La perspectiva top-down presenta tres tipos de procesos. El primer tipo es un efecto directo cross-level, donde los factores a un nivel superior de análisis influencian los resultados o variables dependientes de un nivel menor. El segundo tipo se presenta cuando los factores contextuales pueden moderar relaciones ocurriendo a un nivel menor de análisis, funcionando como moderadores cross-level (Klein et al., 1994; Rousseau, 1985).

El tercer tipo de influencia del contexto se encuentra por la comprensión de una entidad a un menor nivel de análisis en relación a alguna entidad de nivel superior; es decir, cuando el resultado de interés a un nivel menor de análisis es dependiente de alguna variable relativa a un nivel superior (Kozlowski & Klein, 2000; Rousseau, 1985).

En el presente artículo se examina la influencia que las variables de nivel regional tienen sobre el desempeño innovador a nivel de las firmas, estimando efectos directos cross-level y efectos moderadoresmediadores cross-level. Antes de pasar a desarrollar los argumentos teóricos y las hipótesis planteadas en este estudio, se presentan unas consideraciones sobre el método de estimación estadístico adecuado para un enfoque teórico multinivel.

1.2 Ventajas del análisis multinivel en el estudio de la innovación

Una de las afirmaciones más importantes de este estudio es que el ambiente regional, más allá de las diferencias a nivel individual de las firmas, tiene una relación directa sobre la innovación de las firmas. Los nuevos métodos para modelar la innovación han puesto las economías de aglomeración y los vertimientos de conocimiento, especialmente dentro de un contexto espacial, en el centro del análisis (Feldman, 2000). Como Feldman señala: ''el concepto de espacio está ahora siendo definido como una unidad geográfica sobre la cual la interacción y la comunicación es facilitada, la búsqueda intensiva aumentada, y las tareas de coordinación son incrementadas'' (2000, p. 373).

Esta afirmación no es nueva. Es coherente con estudios que han demostrado la incidencia de características regionales en la innovación. Sin embargo, los investigadores del campo de la teoría organizacional y otros investigadores, de áreas como la geografía económica que comparten la preocupación por las dimensiones espaciales de la innovación, estiman los efectos de las características del ambiente regional sobre los resultados de innovación a nivel individual con regresión de mínimos cuadrados ordinarios (OLS, por sus siglas en inglés). Así, estos investigadores (Jaffe, 1986, 1989; Jaffe, Trajtenberg & Henderson, 1993) estiman los efectos del ambiente regional (por ejemplo, gasto en investigación de las universidades y gobiernos, proximidad geográfica, vertimientos, PIB, inversión en I&D, etc.) y las características de firma (por ejemplo, tamaño, edad, redes formales e informales, etc.) sobre una variable dependiente medida en el nivel individual (resultados en innovación, patentes, etc.).

Lamentablemente, las estrategias analíticas convencionales, como los modelos de regresión de mínimos cuadrados ordinarios (OLS), suponen que las observaciones, en este caso las firmas, son independientes. Como resultado, estos modelos ignoran la importancia teórica que un enfoque contextual o emergente (bottom up en este caso) tiene sobre la investigación en innovación, ya que no tiene en cuenta la dependencia que existe entre las firmas que pertenecen a una misma región o grupo (e.g., sector, país). Los modelos de regresión OLS tratan variables de nivel regional (o de grupo) igual que las variables de nivel firma, con todos los miembros de un grupo codificados con los mismos valores para las variables de ambiente regional. Controlando por variables a nivel de región dentro de un nivel individual, el modelo OLS produce un término de error correlacionado para firmas dentro de la misma región. Las estimaciones del modelo OLS deben ser insesgadas; sin embargo, la dependencia dentro de la región entre las firmas produce coeficientes de regresión ineficientes y errores estándar sesgados negativamente (Bryk & Raudenbush, 1992).

Los investigadores han experimentado dificultades con los supuestos que sustentan el modelo de regresión OLS similares a las que se acaban de describir. En general, el modelo OLS se vuelve problemático cuando los investigadores quieren formular y probar hipótesis acerca de cómo las variables de un nivel superior (es decir, ambientales) afectan las relaciones que ocurren en un nivel menor (es decir, individual) (Sniders & Bosker, 1999). Para superar estas dificultades, los investigadores han recurrido a diferentes estrategias estadísticas como el modelo jerárquico lineal, una clase de modelo estadístico que separa intrínsecamente efectos a nivel individual de los efectos a nivel agregado, bajo el supuesto que los datos tienen una estructura jerárquica. En este estudio se construye un modelo estadístico multinivel para determinar la relación entre variables de ambiente regional y variables de nivel firma sobre la innovación.⁵

Por su parte, el empleo de un modelo de regresión multinivel obedece a varias razones. El modelo multinivel extiende las técnicas estadísticas tradicionales al modelar explícitamente el contexto social (Sniders & Bosker, 1999). Esto introduce un grado de realismo a menudo ausente en los modelos de un solo nivel, tales como la regresión múltiple OLS. Muchos de los datos de interés para los investigadores tienen una jerarquía o estructura anidada y los modelos multinivel analizan los niveles de estas estructuras al mismo tiempo. La regresión multinivel modela esta relación entre las observaciones a la vez que proporciona errores estándar insesgados, con lo cual minimiza la probabilidad de cometer el error de rechazar la hipótesis nula cuando ésta es cierta (cometer un error tipo I), al tiempo que estima la variabilidad contextual (entre regiones) de los coeficientes de regresión (Sniders & Bosker, 1999).

De esta manera, el desarrollo de modelos de regresión multinivel ofrece ventajas adicionales sobre investigaciones anteriores que han explorado la relación entre el ambiente regional y características de las firmas sobre la innovación. Entre las principales ventajas de este modelo se encuentra la de reducir problemas conceptuales en cuanto el nivel de análisis al que son deducidos los resultados y las conclusiones. Entre los problemas más conocidos, de la falacia ecológica, el cual consiste en sacar deducciones sobre un nivel individual a partir de datos agregados a un nivel general. En las investigaciones sobre la relación entre regiones e innovación, este es uno de los errores más comunes en el que incurren los investigadores, al no tener en cuenta la naturaleza multinivel de la innovación y al no emplear métodos adecuados de estimación acorde a la estructura de los datos.

1.3 Naturaleza multinivel de la innovación: ambiente regional y desempeño innovador de las firmas

La innovación es un fenómeno de múltiples niveles. Sin embargo, pocas investigaciones directamente la han abordado desde ésta perspectiva. Esto se debe a la falta de marcos de análisis multinivel desarrollados a la investigación sobre el tema de la innovación (Gupta et al., 2007), lo cual ha generado resultados contradictorios.

Dentro de la literatura sobre innovación a nivel regional se destacan dos grandes debates/ problemas. El primero hace referencia a la relación entre ambiente regional y desempeño innovador de las firmas. Aquí se debate en qué medida el ambiente regional constituye una dimensión que influye directamente sobre los resultados de innovación de las firmas. El segundo tiene que ver con una serie de aspectos relacionados (localización espacial de la innovación, vertimientos de información, vertimientos de conocimiento, formas de organización de la innovación y aglomeración espacial) que atañen a las tendencias y la forma en que se configura la innovación a niveles mayores que el nivel de firma. Este artículo se concentra en hacer una prueba empírica sobre el primer debate señalado, dado que los datos disponibles para Colombia todavía no permiten hacer inferencias sobre la dinámica de la innovación desde una perspectiva como la desarrollada aquí.

Diferentes autores sostiene que la dimensión geográfica es fundamental para entender el proceso de innovación en sí mismo (Bathelt, 2005). En este sentido, algunos autores argumentan que la región importa (Gittelman, 2007), siendo central para la comprensión del proceso de innovación analizar el rol de la proximidad espacial y la concentración (Desrochers, 2001). Las regiones son bases importantes de coordinación económica al nivel meso: ''la región está cada vez más incrementado el nivel en el cual la innovación se produce a través de redes regionales de innovadores, clúster locales y los efectos de cruzados de desarrollo de las instituciones de investigación [Trad. Autores]'' (Lundvall & Borrás, 1998, p. 39).

Diversos estudios sostienen que el ambiente regional es crucial para el desempeño innovador de las firmas (Audretsch & Feldman, 2004; Rondé & Hussler, 2005). Con el objetivo de comprender las influencias regionales sobre la innovación de las firmas y las tendencias geográficas en el desarrollo de procesos de innovación, estos estudios han abordado preguntas como: ¿Por qué la ubicación espacial importa a la hora de desarrollar procesos de innovación? ¿Cómo influye el entorno regional de la firma en los resultados de innovación? ¿Cómo se configuran sistemas regionales de innovación y cuál es su papel (potenciar o restringir) en generar procesos de innovación?

No obstante, el rol de la región en la explicación de diferenciales en desempeño innovador de las firmas ha sido puesto en duda. La evidencia no ha sido concluyente debido a la falta de test empíricos que tengan en cuenta las diferencias en los niveles de análisis. Beugelsdijk (2007), por ejemplo, pone a prueba la importancia del rol de la región para el desempeño innovador de la firma. Argumenta que si los investigadores quieren analizar cómo el ambiente de la firma afecta su desempeño, se deben incluir variables de nivel de firma. Los resultados que obtiene le sugieren que los ''los conductores específicos de la firma [Trad. Autores]'' (p. 54) de innovación son más importantes que las variables del ambiente regional de la firma. Propone enfocarse en los actores principales, que son las firmas y sus interrelaciones, particularmente las que involucran intercambio de conocimiento, para estimar en qué medida estas interacciones son llevadas fuera de territorios limitados.

El trabajo de Beugelsdijk (2007) se introduce en el debate acerca de sobredimensionar la importancia de la región y sub-considerar el rol de la firma, aportando evidencia empírica para 1.466 firmas en doce regiones holandesas. Esta investigación parte del hecho que pocos trabajos han intentado relacionar el desempeño innovador de las firmas con variables regionales, con lo cual no se provee una clara distinción entre los efectos específicos de firma y región. En vez de evidencia basada en nivel micro (firma), el argumento que la región importa (Beugelsdijk, 2007) es deducido del macro fenómeno de clústeres de actividad innovadora. Este argumento ha llevado a una falacia ecológica, en la cual un fenómeno global o agregación de datos que son representaciones de fenómenos de un más bajo nivel no pueden ser generalizados a estos bajos niveles.

En la misma vía de Beugelsdijk (2007), Gordon & McCann (2005) critican la visión que sostiene que la innovación es favorecida por la proximidad geográfica. En su estudio, contradicen las hipótesis de las investigaciones centradas en las dimensiones regionales de la innovación (Jaffe et al., 1993), las cuales argumentan que las economías de aglomeración fomentan procesos de aprendizaje dentro de la economía. Particularmente, con base en el estudio de firmas ubicadas en la región de Londres, sostienen que no hay una razón inherente para que una determinada relación entre geografía y organización industrial (clústeres de firmas) debiera ser generalmente superior a configuraciones alternativas (Gordon & McCann, 2005). Dado que el presente estudio es de carácter exploratorio, se propone la siguiente hipótesis para aportar evidencia sobre estas dos visiones de la relación entre ambiente regional y desempeño innovador de las firmas:

Existe una relación positiva y significativa entre las características del ambiente regional, tales como el PIB per cápita, el total de exportaciones de la región, la inversión del gobierno regional en I&D, el número de graduados con titulo de pregrado en la región, el número de investigadores activos en la región y el número de instituciones de educación superior, con el desempeño innovador de las firmas.

2 Método de investigación

2.1 Datos

La muestra está conformada por el número de empresas reportadas en la Segunda Encuesta de Desarrollo e Innovación Tecnológica (EDIT II) para los años 2003-2004,⁶ la cual contiene información sobre el proceso de innovación de 6.670 firmas manufactureras colombianas. Para los datos de ambiente regional se emplea el banco de datos del DANE,⁷ estadísticas del Ministerio de Educación Nacional⁸ y el Ministerio de Comercio, Industria y Turismo,⁹ todas entidades colombianas. A continuación se describen las variables usadas.

2.2 Medidas

2.2.1Variable dependiente

Número de innovaciones de producto ponderadas por objetivos: conteo total de innovaciones en producto de las firmas según lo reportado por la firmas en la EDIT II para los años 2003-2004.

2.2.2 Variables independientes: nivel firma

La fuente de información para todas las variables es la EDIT II para los años 2003-2004.

• Redes formales de innovación de la firma: número de vínculos totales mediados por dinero que la firma posee con diferentes actores.

• Redes informales de innovación de la firma: número de vínculos totales que la firma reconoce como fuentes de ideas para la innovación que no están necesariamente mediadas por dinero.

• Capacidad de coordinación interna para la innovación: número de vínculos totales, las redes internas o fuentes de información para la innovación dentro de la firma.

• Inversión en I&D: gasto en actividades de la firma en I&D.

• Tamaño de la firma: número de empleados de la firma.

• Personal ocupado técnico: razón del número de empleados con formación técnica sobre el número total de empleados.

• Personal ocupado profesional: razón del número de empleados con formación profesional sobre el número total de empleados. Capital extranjero: porcentaje de capital extranjero de la firma.

2.2.3Variables independientes: nivel región

• PIB per cápita: promedio de los años 2002- 2003-2004 PIB PC departamental a precios constantes, según lo reportado en las Cuentas Nacionales Departamentales de la base de datos del DANE de Colombia.

• Graduados pregrado: número de habitantes que se graduaron en el respectivo año con titulo de pregrado en la región. Promedio años 2002-2003-2004, según lo reportado por el Ministerio de Educación Nacional de Colombia.

• Inversión del gobierno en I&D: inversión del gobierno central en I&D para las entidades territoriales, millones de pesos de 2008. Promedio años 2002-2003-2004, según lo reportado en los indicadores de Ciencia y Tecnología para Colombia.¹⁰

• Instituciones de educación superior: número de establecimientos de educación superior en la región. Promedio años 2002- 2003-2004, según lo reportado por el Ministerio de Educación Nacional de Colombia.

• Investigadores activos: número de investigadores activos en la región. Promedio años 2002-2003-2004, según lo reportado en los indicadores de Ciencia y Tecnología para Colombia.

• Total exportaciones de la región: promedio de los años 2002-2003-2004 del volumen de exportaciones regionales medido en miles de dólares para cada región del país, según lo reportado por el Ministerio de Comercio, Industria y Turismo de Colombia.

2.3 Modelo de regresión Poisson multinivel

2.3.1 Los modelos para variables dependientes de conteo

Generalmente las variables de conteo (la variable dependiente de este estudio) son tratadas como si fueran continuas. Al utilizar una regresión lineal a variables de conteo como si fueran continuas se pueden generar problemas en la estimación de los parámetros con resultados infaustos en la eficiencia, consistencia y sesg0 de los estimadores (Long, 1997). No obstante, existen modelos que se han diseñado para aplicarse a variables dependientes de conteo en este caso, el número de innovaciones por producto ponderadas por objetivos de las firmas. El modelo de Poisson, el más básico de los modelos aplicados a estas características, sirve para tener en cuenta la estructura de la variable dependiente. El número de innovaciones de la EDIT II es una variable de conteo, discreta y posee valores no negativos. Por lo tanto, es posible postular que su distribución se ajusta a las características de un proceso de Poisson. Siguiendo a Winkelmann (2008), los modelos Poisson se caracterizan por presentar equidispersión, es decir, su media y su varianza son iguales, y porque la probabilidad de un conteo es determinada por una distribución Poisson, donde la media de la distribución es una función de las variables independientes (Long, 1997). Winkelmann (2008) argumenta que si y es una variable aleatoria con una distribución discreta definida en N,U {0} = {0,1,2...}, entonces el conjunto Y tiene una distribución de Poisson con parámetro μ, escrita como X~Po(μ), si la función de probabilidad es:

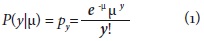
Para μ que pertenece a los reales positivos y, y=0,1,2, ..., y la función de probabilidad está dada por:

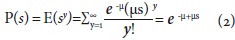
Se puede calcular el valor esperado o primer momento de la distribución y su varianza:

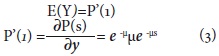
Si s=1, se puede decir que:

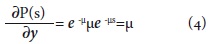
Por otra parte, la varianza es igual a:

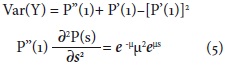
Si s=1, se puede decir que:

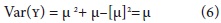
Estos resultados permiten evidenciar la característica particular de un modelo Poisson: su equis-dispersión. En la práctica, tal como sucede con el conteo de innovaciones (se distribuye Poisson), de acuerdo con el Gráfico 1 y las estadísticas descriptivas (ver Tabla 1), la varianza excede la media y existe un alto porcentaje de ceros en la distribución, lo cual indica una sobre-dispersión de los datos (varianza mayor que la media). La evidencia empírica demuestra que el modelo Poisson raramente predice esto en la práctica, lo cual genera que el modelo Poisson deje de ser en sí mismo el mejor modelo. Sin embargo si lo cálculos de la media son correctos, existe sobre-dispersión y los estimadores de un modelo Poisson son consistentes pero ineficientes (Long, 1997).¹¹

De acuerdo a la Tabla 1 existen muchas observaciones de cero en la variable dependiente de este estudio (18,7%). Sin embargo, esto no es problema porque un valor de cero en la variable endógena tiene dos posibles interpretaciones. Por un lado, los modelos inflados de ceros pueden proporcionar mejores resultados que los modelos de Poisson y/o binomial negativo, ya que éstos no tienen en cuenta en la estimación, esos posibles aspectos diferenciadores. Por otro lado los inflados de ceros suponen que la variable dependiente es el producto de una ley binaria y una ley de Poisson o binomial negativa (Melgar, Ordaz & Guerrero, 2005). De acuerdo a Melgar et al. (2005), la idea en la que se basan estos modelos más complejos es el que la población consta de dos tipos de individuos: para una parte de ellos, la observación es siempre nula mientras que, para el resto, los resultados se generan según la distribución de Poisson o binomial negativa, según se considere.

Subyace así una decisión inicial de participación de cada individuo representada por la variable X. Sin participación (x_i= 0), Y vale 0; cuando hay participación (x_i=1), se conduce según la ley elegida, pudiendo también, en particular, anularse. La posibilidad de que se obtengan valores nulos para la variable dependiente por estas dos vías, conlleva que el porcentaje de ceros observados sea elevado. Si z_j es la probabilidad que la variable dependiente siempre tome valores de cero, se tiene así que:

Una manera de aplicar el problema de los excesivos ceros en la distribución de la variable consiste en aplicar un modelo Poisson inflado de ceros o ZIP. El ZIP toma en cuenta las generalidades del modelo Poisson, con una cierta aclaración en términos probabilísticos sobre los excesivos ceros de la distribución. Este modelo tiene en cuenta la probabilidad, (1-z_j), que la variable dependiente siempre tome valores de cero y una probabilidad, (1- z_j), que la variable dependiente, a pesar de que contenga observaciones cero, provenga de una distribución Poisson.

Detalladamente, la variable dependiente, y_i, será cero sí y solo si:

• Tiene una probabilidad zi con la que y_i=0,

• Tiene una probabilidad (1-zi) de que y_i > 0 provenga de una distribución Poisson, es decir,

Por lo que la probabilidad de encontrar valores ceros provenientes de una distribución Poisson será:

Así, el hecho que y_i=0, procedente de la probabilidad z_i y del proceso Poisson es:

Por otra parte, encontrar un valor que sea mayor a cero, será con una probabilidad (1–z_i) igual a:

Donde μ_i y z_i pueden especificarse de varias maneras; sin embargo, siguiendo a Lambert (1992), se asume que μ_i y z_i se modelan cumpliendo las siguientes distribuciones:

Interpretando las distribuciones de Lambert (1992) se puede decir que el modelo ZIP se descompone en dos modelos. El primero estima un modelo de Poisson estándar, existan o no valores nulos en la distribución. El segundo modelo es un logit que permite definir la probabilidad de no innovar por dos vías: hay algunas firmas con características similares en las variables independientes, que no innovaron, y otras que no tienen características similares. De esta forma, el modelo logit solo contiene firmas que no innovaron y cuyo objetivo de innovación se reflejó en no seguir la misma estratégia definida y por ende no lograron hacer nada a pesar de tener las mismas características o en intentar tener la estrategia teniendo características similares, pero no lograr por lo menos una innovación.

Es necesario aclarar que la media y la varianza de este modelo ZIP, son respectivamente:

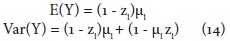
Solo en el caso que z_i=0 el modelo es igual al Poisson estándar.

Existe la alternativa del modelo binomial negativo inflado de ceros o ZINB, donde la distribución de probabilidades se formula como:

1 El hecho que y_i=0, procedente de la probabilidad z_i y del proceso Binomial negativo es:

2 Encontrar un valor que sea mayor a cero, será con una probabilidad (1–z_i) igual a:

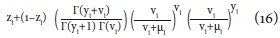
Las implicaciones son similares a las de un modelo ZIP y el parámetro v_i es conocido como el parámetro de dispersión. Hasta el momento se puede argumentar que los modelos inflados de ceros superan el problema de excesos de cero, pero no resuelve el problema de la dimensión multinivel que caracteriza a la innovación. Tener en cuenta los excesos de cero en la variable dependiente del estudio (conteo de innovaciones en producto de las firmas) resulta acorde con las características de la innovación en países como Colombia, dado que la mayoría de firmas no tienen resultados en innovación. No tener en cuenta esta característica en la formulación del modelo de regresión conlleva errores en la estimación de los parámetros del modelo.

2.3.2 Los modelos multinivel con intercepto y coeficientes aleatorios

Como se ha sostenido a lo largo de estas líneas, los datos de la investigación en innovación con frecuencia se estructuran de manera jerárquica. Por ejemplo, los datos pueden consistir en firmas anidadas dentro de sectores, que a su vez se pueden anidar en los departamentos o regiones geográficas. El ajuste de modelos de regresión Poisson o ZIP que ignoran la estructura jerárquica de los datos puede llevar a conclusiones falsas. La implementación de un análisis estadístico que toma en cuenta la estructura jerárquica de los datos requiere métodos especiales y, al comparar los modelos resultantes, las inferencias falsas se pueden extraer al tener en cuenta la estructura anidada de los datos.

Los datos empleados en este estudio tienen una estructura jerárquica, con variables medidas a nivel firma y a nivel región. Las firmas se agrupan dentro de unidades geográficas como las regiones. Las firmas dentro de un mismo grupo (región) a menudo son más parecidas que dos firmas elegidos al azar, ya que probablemente tenga algún tipo de correlación de las variables importantes. Por ejemplo, las firmas innovadoras de un departamento pueden tener características socio-demográficas particulares que las hacen similares. Igualmente, las firmas de una misma región están sometidas a las mismas presiones ambientales, lo que hace probable que compartan características similares que las diferencian de firmas ubicadas en otras regiones.

Los métodos estadísticos tradicionales ignoran la correlación de los resultados dentro de los grupos (regiones) y tienden a subestimar los errores estándar. Esto aumenta artificialmente la importancia de las pruebas de hipótesis, lo que aumenta el riesgo de inferir la falsa conclusión de que existen asociaciones significativas. Además, no permiten incorporar características medidas en diferentes niveles de la jerarquía (Austin, Goel & Walraven, 2001). El propósito de un análisis multinivel, en este sentido, consiste en incorporar las variables medidas en los diferentes niveles de la jerarquía, y examinar cómo las relaciones de regresión varían a través de los grupos (regiones).

Al evaluar las innovaciones ponderadas por objetivos en el nivel más bajo de la jerarquía, con variabilidad de las relaciones de regresión a través de las regiones, las técnicas de análisis de regresión jerárquica (intercepto aleatorio o coeficientes aleatorios) presentan ventajas (Austin et al., 2001). Por ejemplo, si el interés es el efecto de las características medidas en niveles superiores de la jerarquía de los datos (regiones), el análisis multinivel es el adecuado (Austin et al., 2001).

Los datos de este estudio constan de firmas anidadas dentro de regiones. Se puede suponer que entre las variables construidas se encuentra el porcentaje de capital extranjero de cada firma, y el resultado es el conteo de una innovación ponderada por objetivo. Con el fin de simplificar la interpretación de los coeficientes de regresión, el porcentaje de capital extranjero de cada firma se centra en la media de cohorte (el porcentaje de capital extranjero de cada firma, menos el promedio del porcentaje de capital extranjero de cada firma).

Si un modelo tradicional de regresión Poisson se ajusta a los datos, el término de intersección es el conteo promedio de innovaciones ponderadas por objetivos de la firma para una firma con un porcentaje de capital extranjero promedio (porcentaje de capital extranjero = 0, ya que el porcentaje de capital extranjero está centrado).

La pendiente es la cantidad en que aumenta las innovaciones ponderadas por objetivos de la firma por cada aumento porcentual de capital extranjero, manteniendo lo demás constante. En este modelo, la única fuente de variación es la variación alrededor de la línea de regresión. Un modelo de regresión tradicional asume que los sujetos son independientes el uno del otro. Sin embargo, este modelo pasa por alto el hecho de que las firmas de una misma región no pueden ser independientes, ya que el resultado (las innovaciones ponderadas por objetivos) depende en gran medida de las características de la región. Así mismo, una región podría atraer a las firmas menos innovadoras, lo que aumenta su costo de innovación. Por lo tanto, una mayor homogeneidad puede ocurrir dentro de una determinada región de lo se podría esperar de manera aleatoria. No tener en cuenta este hecho puede dar lugar a estimaciones incorrectas de los errores estándar de los coeficientes.

Si se utilizaran los modelos tradicionales de regresión también se asumiría, para el ejemplo, que el efecto del porcentaje de capital extranjero sobre las innovaciones ponderadas por objetivos es el mismo para todas las regiones. En realidad, el efecto del porcentaje de capital extranjero sobre los resultados puede variar según las regiones y es por esta razón que los modelos Poisson y ZIP tradicionales son de utilidad limitada y pueden generar resultados dudosos cuando se utiliza en una situación jerárquica. Además, los modelos tradicionales de regresión no permiten incorporar características a nivel de regiones, debido a que genera una interpretación igual entre variables de diferentes niveles o jerarquías.

Aplicando el modelo multinivel se pueden interpretar y realizar estimaciones correctas al tener en cuenta un intercepto o un coeficiente aleatorio. Un modelo de intercepto aleatorios incorpora la naturaleza jerárquica de los datos, con una línea de regresión por separado para las firmas de cada región, y con líneas de regresión por regiones, restringidas a tener la misma pendiente. Por lo tanto, las relaciones entre las variables de predicción y los resultados se ven obligadas a ser las mismas para cada región. Un modelo de intercepto aleatorio tiene importancia sólo si interesan las características a nivel de firma y si las innovaciones ponderadas por objetivos para una firma promedio varían entre las regiones, dejando el efecto de cada característica a nivel de firma igual para las firmas en cada región.

El modelo de coeficientes aleatorios incorpora la estructura jerárquica de los datos y permite tener una mejor comprensión de las relaciones subyacentes en los datos. En un modelo de coeficientes aleatorios, un modelo de regresión por separado es ajustado para las firmas en cada región. En contraste con el modelo de intercepto aleatorios, todos los coeficientes de regresión pueden variar entre modelos específicos por región. Como en el modelo de intercepto aleatorios, cada modelo se supone que es similar a los otros modelos, y la línea de regresión en cada región se comprime hacia el modelo de regresión promedio. El efecto de esto es que la línea de regresión de cada región es un compromiso entre la línea de ajuste de regresión, a través de firmas de la región, y la relación de regresión promedio de todas las regiones.

Al ajustar un modelo de coeficientes aleatorios también se puede examinar la correlación entre los coeficientes de regresión estimados. Se puede ajustar un modelo de coeficientes aleatorios si interesan las características a nivel de firma y si se quiere permitir que el efecto de al menos una de las características de la firma varíe entre las regiones. Las características de estos modelos indican que el intercepto es variable, lo que indica que las innovaciones ponderadas por objetivos de la firma varían según las regiones. También, la pendiente de la recta de regresión varía, por tanto, el cambio en las innovaciones ponderadas por objetivos por aumento del porcentaje de capital extranjero varía entre las regiones. Por último, existe una correlación negativa entre el origen y la pendiente, ya que las líneas de regresión con bajos interceptos tienden a tener mayor pendiente.

Aplicado a este estudio, se puede argumentar bajo un modelo de regresión Poisson, un intercepto aleatorio ς_1j que defina la dependencia entre las firmas (j) de una región específica (i):

Donde (ς_1j| x_ij)~N(0,ψ₁₁) y ς_1j son independientes entre las firmas j. El intercepto aleatorio en términos exponenciales, exp(ς_1j), es llamado alguna veces como el término de fragilidad (Rabe-Hesketh & Skrondal, 2008). El número de innovaciones ponderadas por objetivos y_1j y y_2j para una firma j, en las dos ocasiones, son especificados como condicionalmente independientes dado el intercepto aleatorio y las variables.

De igual manera, los modelos multinivel Poisson inflados de cero con intercepto y coeficiente aleatorio, incorporan un coeficiente aleatorio a nivel de firmas, ς_2j, para el capital extranjero x_2i:

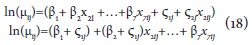
De acuerdo a Rabe-Hesketh & Skrondal (2008), dadas las variables, el coeficiente e intercepto aleatorio tienen una distribución normal bivariada con media cero y matriz de covarianza:

En términos de valor esperado, este modelo se interpreta como:

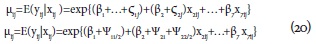
Aunque se soluciona el problema de interpretación e inclusión jerárquica, algunas muestras de variables dependientes que se distribuyen Poisson presentan excesos de ceros, por lo que un modelo Poisson no es la mejor opción por las inferencias erróneas. Un enfoque popular para el análisis de estos datos es usar un (ZIP) modelo de regresión Poisson inflado de ceros, anunciado anteriormente. Dado el diseño jerárquico, la inflación de ceros y la falta de independencia pueden ocurrir al mismo tiempo, lo que hace al modelo estándar ZIP inadecuado, siendo necesario y plausible un modelo ZIP multinivel con efectos aleatorios (coeficientes e intercepto) para hacer frente a una estructura de correlación más compleja.

Según Lee & Wang (2006), el modelo ZIP multinivel con intercepto y coeficientes aleatorios es parecido al ZIP tradicional de Lambert (1992), solo que incorpora un conjunto de componentes aleatorios para el intercepto y coeficiente. Tradicionalmente este tipo de modelos pueden ser generados a partir de una aproximación de un modelo mixto lineal generalizado mediante la técnica de máximo de verosimilitud.

3 Resultados y discusión

En la Tabla 2 se reportan los resultados aplicados a los modelo de regresión lineal, Poisson, binomial negativo y ZIP sin tener en cuenta los efectos jereraquicos ni aplicar el analisis multinivel.

En la Tabla 2 se observa la sobreestimacion de los parametros cuando se realiza una regresion por mínimos cuadrados ordinarios. A partir de los modelos Poisson, binomial negativo y ZIP, se encuentra cierta estabilidad de estos resultados. Sin embargo, los resultados de las variables de segundo nivel no estan siendo tratadas como tal, por lo que sería errado desarollar una interpretación de estos resultados.

Un resultado interesante se encuentra al incoroporar el concepto de jerarquía (ver Anexo Tabla A1) con los ejercicios aplicados a los modelos multinivel Poisson con intercepto aleatorio (Poisson RI), con intercepto y coeficiente aleatorio (Poisson RIRC), y Modelos ZIP multinivel con intercepto y coeficiente aleatorio (MZIPRIRC). De hecho, los parametros en las variables de segundo nivel son más pequeños y el coeficiente de determinación es mejor que los modelos de la Tabla 1. Como es evidente en la muestra, la variable tiene exceso de ceros por lo que un modelo ZIP multinivel con intercepto y coeficiente aleatorio resulta con un ajuste del 15,9%, mientras que la parte multinivel logística presenta el mejor ajuste del modelo (R²=0,347).

Coherente con la teoria Schumpeteriana, un mayor tamaño de la firma permite obtener mayor número de innovaciones ponderadas por objetivos y disminuye la probabilidad de no realizar innovaciones. Asi mismo, las redes formales e informales importan en el momento de realizar innovaciones ponderadas, pero solo los vinculos de tipo formal importan en el aumento de la probabilidad de innovar.

No se puede desconocer el rol de las capacidades internas de coordinación en el desempeño innovador. Con el segundo coeficiente más alto de las variables de primer nivel, esta variable explica en gran medida el número de resultados de innovación y la probabilidad de que una firma tenga el potencial de innovar. En la medida en que haya más recursos internos y financieros, la firma tiene mayor probabilidad de innovar pues cuenta con más recursos y agentes internos involucrados y comprometidos con el proceso de innovación, los cuales producen más ideas y potencializan la coordinación interna de la empresa.

En cuanto al capital humano incorporado en el proceso de innovación de las empresas, se puede argumentar que a mayor grado de formación educativa, hay mayor influencia en el desempeño innovador; pero a menor grado de formación se influye significativamente en la probabilidad de innovar. Este resultado implica que el proceso de innovación requiere, en cuanto a formación educativa, de un punto de partida mínimo para hacer más probable el desempeño innovador positivo pero requiere a su vez un mayor grado de desarrollo de capital humano para mantener (e incluso aumentar) el desempeño innovador.

Los resultados de la Tabla 2 indican que existen algunas variables regionales (o de segundo nivel) que generan impactos sobre el desempeño innovador y la probabilidad de innovación. Mientras que las exportaciones generan un mayor desempeño innovador, el ingreso por habitante genera una caída, por efectos de costo de oportunidad en el número de innovaciones. En este sentido, se prueba parcialmente la hipótesis de que las características favorables del ambiente regional tiene un efecto positivo y significativo sobre el desempeño innovador de las firmas en el país.

4 Conclusiones

El análisis aquí realizado aporta una serie de evidencias que avanzan en la comprensión de la naturaleza multinivel de la innovación. Los resultados generales confirman parcialmente que el ambiente regional tiene una relación directa sobre el desempeño innovador de las firmas. Los procesos de innovación dependen de características tanto de la firma como del ambiente en las cuales aquellas operan. Esto da lugar a una diferenciación en términos de desempeño innovador en las regiones del país, tanto a nivel firma como a nivel región.

Uno de los principales aportes de esta investigación reside en establecer estadísticamente, mediante un modelo estadístico multinivel, que las variables ambientales tienen una relación directa con la innovación a nivel de las firmas, lo cual contradice investigaciones anteriores (Beugelsdijk, 2007). Las variables de nivel regional explican parte de la varianza en diferenciales de desempeño innovador de las firmas. Usando datos sobre las características de las firmas y el ambiente regional en un modelo multinivel, se confirma que las capacidades de innovación de las firmas son importantes, pero también las características del ambiente regional en los resultados de innovación empresarial.

En Colombia se comienza a disponer de datos a nivel de firmas para la investigación sobre la innovación, lo cual implica un esfuerzo y debate alrededor de los niveles apropiados de análisis (institucionales, sectoriales, regionales, locales, organizacionales, etc.) para probar varios tipos de hipótesis. Como se sustentó al inicio, el enfoque típico es ignorar la estructura jerárquica de los datos sobre innovación, incluir dummies sectoriales o regionales, o simplemente ignorar los diferentes niveles involucrados en el desarrollo de los procesos de innovación.

Este estudio avanza en la comprensión de la innovación empresarial en Colombia. No obstante, aún existe una considerable heterogeneidad entre las diferentes regiones que constituyen vacíos por explicar. Muchas de las condiciones ambientales no exploradas en este estudio (como por ejemplo, expectativas, diferencias culturales, rasgos sociales, capital social, confianza, entre otras), pueden ser analizadas. Naturalmente, los estudios cuantitativos tienen límites, lo cual hace necesario un llamado al desarrollo de estudios cualitativos desde la perspectiva multinivel.

El objetivo principal de este estudio ha sido evidenciar el análisis multinivel como un método promisorio para la investigación sobre la naturaleza contextual de la innovación. Aunque existen hipótesis que no requieren análisis multinivel explícitos, existen muchas hipótesis que requieren considerar las relaciones entre diferentes niveles de análisis. El problema de la unidad de análisis puede ser abordado en la investigación empírica construyendo modelos multiniveles de la innovación. Estos modelos se pueden extender más allá del desarrollado en este estudio, incorporando interacciones entre variables de diferentes niveles, lo cual permitirá entender la variedad en la configuración de sistemas de innovación. Igualmente, se pueden desarrollar modelos con una estructura jerárquica más compleja, como por ejemplo, que tengan en cuenta el nivel firma, región y sector. Las investigaciones avanzarían considerablemente al comprender la naturaleza dinámica y compleja de la innovación mediante el examen tanto de los procesos bottom-up y top-down. Este estudio es un primer intento de desarrollar la perspectiva multinivel aplicada a la innovación empresarial en el país.

NOTAS

3 ''Sólo el 10% de todos los artículo sobre innovación publicados durante 1990-2006 en cinco revistas claves en administración realizaron algún tipo de análisis multinivel empírico [Trad. Autores]'' (Gupta et al., 2007, p. 885).

4 Perspectiva propuesta teóricamente a propósito de la innovación, pero poco abordada empíricamente.

5 Los autores agradecen a los revisores anónimos la aclaración relacionada con otras fuentes de correlación en estudios empíricos que involucran la dimensión geográfica. Una de ellas, la auto correlación espacial, que puede ser abordada con técnicas estadísticas como la econometría espacial (Anselin, 2010; Varga, 2006).

6 Disponible en Segunda Encuesta de Desarrollo e Innovación Tecnológica: http://www.dane.gov.co/index.php?option=com_contentview=articleid=104Itemid=61.

7 DANE hace referencia a las siglas para ''Departamento Administrativo Nacional de Estadística'' en Colombia. Disponible en DANE: http://www.dane.gov.co/#twoj_fragment1-4.

8 Disponible en Ministerio de Educación Nacional: http://www.mineducacion.gov.co/1621/w3-channel.html.

9 Disponible en Ministerio de Comercio, Industria y Turismo: https://www.mincomercio.gov.co/

10 Disponible en Indicadores de Ciencia y Tecnología http://ocyt.org.co/html/

11 Los estimadores deben ser insesgados o centrados, es decir, que su sesgo sea nulo, por ser su esperanza igual al parámetro que se desea estimar, eficiente o más preciso que otro estimador; es decir, si la varianza del primero es menor que la del segundo. A medida que el tamaño de la muestra crece, el valor del estimador tienda a ser el valor del parámetro y la varianza de este sea cero, o sea, consistentes. También deben ser robustos y suficientes, es decir, suficiente cuando resume toda la información relevante contenida en la muestra, de forma que ningún otro estimador pueda proporcionar información adicional sobre el parámetro desconocido de la población.

Referencias bibliográficas

Anselin, L. (2010). Thirty Years of Spatial Econometrics. Papers in Regional Science, 89(1), 3–25.

Audretsch, D. & Feldman, M. (2004). Knowledge spillovers and the geography of innovation. En P. Nijkamp (Ed.), Handbook of regional and urban economics (Vol.4, Ch. 61, pp. 2713-2739). Amsterdam, New York, North-Holland: Elsevier.

Austin, P., Goel, V. & Walraven, C. (2001). An Introduction to Multilevel Regression Models. Revue Canadienne de Santé Publique, 92(2), 150-154.

Bathelt, H. (2005). Cluster relations in the media industry: Exploring the ''distanced neighbor'' paradox in Leipzig. Regional Studies, 39(1), 105-127.

Beugelsdijk, S. (2007). The regional environment and a firm's innovative performance; a plea for a multilevel interactionist approach. Economic Geography, 83(2), 181-199.

Bryk, A.S. & Raudenbush, S.W. (1992). Hierarchical Linear Models. Applications and Data Analysis Methods. Newbury Park, CA: Sage.

Desrochers, P. (2001). Geographical Proximity and the Transmission of Tacit Knowledge. Review of Austrian Economics, 14(1), 25-46.

DiMaggio, P.J. & Powell, W.W. (1991). Introduction. En W.W. Powell & P.J. DiMaggio (Eds.), The new institutionalism in organizational analysis (pp. 1–38). Chicago, IL: University of Chicago Press.

Feldman, M.P. (2000). Location and Innovation: The New Economic Geography of Innovation, Spillovers, and Agglomeration. En G. Clark, M. Feldman & M. Gertler (Eds.), The Oxford Handbook of Economic Geography (pp. 373-394). Oxford, UK: Oxford University Press.

Gittelman, M. (2007). Does Geography Matter for Science-Based Firms? Epistemic Communities and the Geography of Research and Patenting in Biotechnology. Organization Science, 18(4), 724-745.

Gordon, I.R. & McCann, P. (2005). Innovation, agglomeration, and regional development. Journal of Economic Geography, 5(5), 523-543.

Gupta, A., Tesluk, P. & Taylor, M. (2007). Innovation At and Across Multiple Levels of Analysis. Organization Science, 18(6), 885-897.

Jaffe, A. (1986). Technological opportunity and spillovers of R&D. American Economic Review, 76(5), 984-1001.

Jaffe, A. (1989). The real effects of academic research. American Economic Review, 79(5), 957-970.

Jaffe, A., Trajtenberg, M. & Henderson, R. (1993). Geographic localization of knowledge spillovers as evidence by patent citations. The Quarterly Journal of Economics, 108(3), 577-598.

Klein, K.J., Dansereau, F. & Hall, R.J. (1994). Levels issues in theory development, data collection, and analysis. Academy Management Review, 19(2), 195–229.

Kozlowski, S.W.J. & Klein, K.J. (2000). A multilevel approach to theory and research in organizations: Contextual, temporal, and emergent processes. En K.J. Klein & S.W.J. Kozlowski (Eds.), Multilevel Theory, Research, and Methods in Organizations (pp. 3-90). San Francisco, CA: Jossey-Bass.

Lambert, D. (1992). Zero-inflated Poisson regression, with an application to defects in manufacturing. Technometrics, 34(1), 1-14.

Lawrence, P.R., & Lorsch, J.W. (1967). Organization and environment: Managing differentiation and integration. Boston, MA: Harvard Business School Press.

Lee, A. & Wang, K. (2006). Multilevel zero inflated Poisson regression modeling of correlated count data with excess zeros. Statistical Methods in Medical Research, 15(1), 47-61.

Long, J.S. (1997). Regression Models for Categorical and Limited Dependent Variables. Advanced Quantitative Techniques in the social Sciences series. Thousand Oaks, CA: Sage.

Lundvall, B.A. & Borrás, S. (1998). The Globalising Learning Economy: Implications for Innovation Policy. Targeted Socio-Economic Research Studies, DG XII, Commission of the European Union. Luxembourg: Office for Official Publications of the European Communities.

Melgar, M.C., Ordaz, J.A. & Guerrero, F.M. (2005). Diverses alternatives pour déterminer les facteurs significatifs de la fréquence d'accidents dans l'assurance automobile. Insurance & Risk Management, 73(1), 31-54.

Rabe-Hesketh, S. & Skrondal, A. (2008). Multilevel and Longitudinal Modeling Using Stata (2a ed.). College Station, TX: Stata Press.

Rondé, P. & Hussler, C. (2005). Innovation in regions: What does really matter?. Research Policy, 34(8), 1150-1172.

Rousseau, D.M. (1985). Issues of level in organizational research: Multi-level and crosslevel perspectives. En L.L. Cummings & B. Staw (Eds.), Research in Organizational Behavior (Vol. 7, pp. 1-38). Greenwich, CT: JAI Press.

Scott, W.R. (2003). Organizations: Rational, natural, and open systems. Englewood Cliffs, NJ: Prentice Hall.

Sniders, T. & Bosker, R. (1999). Multilevel analysis. An introduction to basic and advanced multilevel modeling. Thousand Oaks, CA: Sage Publications.

Varga, A. (2006). The Spatial Dimension of Innovation and Growth: Empirical Research Methodology and Policy Analysis. European Planning Studies, 14(9), 1171-1186.

Winkelmann, R. (2008). Econometric Analysis of Count Data (5a ed.) New York, NY: Springer Press.

ANEXOS

Anexo 1. Modelos multinivel Poisson y ZIP co interceptos y coeficientse aleatorios.