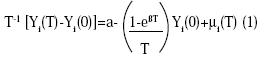
CRECIMIENTO Y CONVERGENCIA: A PROPÓSITO DE QUAH*
JHON JAMES MORA
Economista, Universidad del Valle, M.A. Universidad Autónoma de Madrid, Ph.D(c) Universidad Alcalá de Henares. Profesor tiempo completo del Departamento de Economía de la Universidad Icesi. e-mail: jjmora@icesi.edu.co.
Fecha de recepción: 30-5-2003 Fecha de aceptación: 20-8-2003
*Agradezco los comentarios de José Javier Núñez, de la Universidad Alcalá de Henares, y del evaluador. También agradezco la invaluable ayuda de Isaías Salgado, de la Universidad Autónoma de México, con las rutinas warpdem.ado y silvetest.ado del programa STATA.
ABSTRACT
This paper discusses the results of Quah´s work on convergence between countries. The results show that, although Quah´s work regarding beta and sigma convergence is overwhelming, his stochastic core estimate is fairly controversial. Therefore, the transition between countries is reduced to a one-step Markov chain.
KEY WORDS
Growth, convergence, unit root, stochastic core, Markov chains.
RESUMEN
Este artículo discute los resultados del trabajo de Quah sobre la convergencia entre países. Los resultados muestran que aunque el trabajo de Quah es demoledor en torno a la convergencia tipo beta y sigma, la estimación del núcleo estocástico es bastante discutible y, por lo tanto, la transición entre países queda reducida a una cadena de Markov de un paso.
PALABRAS CLAVES
Crecimiento, convergencia, raíz unitaria, núcleo estocástico, cadenas de Markov.
Clasificación Colciencias: A; JEL
Classification: C1, O4.
INTRODUCCIÓN
Durante la década de los años noventa se llevó a cabo una de las más interesantes discusiones en el campo del crecimiento económico: converge o no converge el PIB de los países en el tiempo. Por un lado, la ortodoxia tradicional, como respuesta a los trabajos de los años ochenta que mostraban la no-existencia de convergencia absoluta, produjo la idea de la convergencia condicional de la mano de Barro y Sala-I-Martín (1992b) y, entonces, los países pobres convergerían hacia los países ricos a una tasa de crecimiento del 2% anual. La reacción, propuesta por los artículos de Quah (1993, 1996a, 1996b, 1997) fue demoledora e irrebatible: no existe convergencia a una distribución única, todo lo contrario, los países ricos cada vez serán más ricos y los pobres cada vez más pobres.
Diez años después de la publicación del primer artículo de Quah, aquí se analizará en qué consistió la crítica realizada por Quah a la convergencia entre países tipo beta y sigma y se discutirá la idea de la transición estocástica de los países. De esta forma, en la primera sección se introduce a la discusión sobre las diferentes medidas de convergencia. En la segunda sección se discute la idea de la convergencia condicional y su relación con las raíces unitarias, la convergencia tipo sigma y la falacia de Galton. En la tercera sección se presenta la idea de los clubes de convergencia así como la estimación de la distribución del PIB para 1960, 1985 y 2000 usando el núcleo gausiano y se calcula el número de modas de acuerdo con la prueba de multimodalidad de Silverman (1986), encontrando que la distribución en 1960 es unimodal mientras que en 1985 y 2000 es bimodal. Cuando se calcula la distribución ergódica se encuentra, al igual que Quah, que ésta es bimodal y no unimodal. Sin embargo, este resultado se debe a las propiedades de una cadena Markoviana y no de un núcleo estocástico como sostiene Quah. En la última sección se presentan las conclusiones.
1. HIPÓTESIS DE CONVERGENCIA Y LA CONVERGENCIA AL ESTADO ESTABLE
La discusión sobre la convergencia tiene sus orígenes en el análisis sobre el crecimiento y el arribo al estado estable de aquellos países más atrasados, expresados en el modelo Solow-Swan. Parte de asumir que existen fuerzas automáticas que llevan a una convergencia en el tiempo en los niveles del PIB como lo señalan Barro y Sala-I-Martín (1992 Pág. 223). ¿Cuáles son esas fuerzas? Sin duda, la competencia y los rendimientos, decrecientes a la acumulación de capital. Sin embargo, una vez situados en el plano específico de la teoría del crecimiento, las fuerzas de las que hablan Barro y Sala-I-Martín no son, en realidad, las fuerzas de la competencia sino las resultantes del uso de una función de producción neoclásica, definida según las exigencias usuales de esta teoría: Homogeneidad de grado 1, concavidad y rendimientos decrecientes a los factores individuales [Mora y Salazar (1994)].
En el terreno de la discusión empírica, imponer estos supuestos implica más de lo que parece, como bien lo señaló Cohen (1995), pues el primer problema de este tipo de formulación consiste en que sólo sirve para estimar los coeficientes de la función de producción subyacente, pero no es útil para dar cuenta de la existencia de un estado estable real de la economía, ni de la velocidad de la convergencia hacia ese supuesto estado estable. La critica a Cohen (1995) proviene desde luego de Sala-I-Martín (2000) para quien el modelo neoclásico no hace predicción sobre la convergencia y la evidencia, por lo tanto, no puede ser una crítica al modelo en sí.
Para Sala-I-Martín (2002) el modelo neoclásico predice que la tasa de crecimiento de una economía está inversamente relacionada con la distancia que la separa de su propio estado estacionario y solamente en el caso de que todas las economías se acerquen al mismo estado estacionario esta predicción es equivalente a la de que las pobres crecerán más que las ricas.
El análisis tradicional de la hipótesis de convergencia se encuentra en Barro y Sala-I-Martín (1992a). El fundamento empírico de la converconvergencia entre países consiste en una regresión de convergencia que proviene de linealizar las ecuaciones de crecimiento del consumo (regla Ramsey- Keynes) y del stock de capital. La ecuación de convergencia muestra el crecimiento explicado por los niveles del PIB. Siguiendo a Sala-I-Martín (2000) la ecuación de convergencia será:
En la ecuación 1 Yi es el logaritmo del PIB en el país i, 0 es el año inicial, T es el año final, a es una constante que depende de los parámetros tecnológicos del modelo y β es el coeficiente de convergencia: la tasa a la cual una economía se aproxima al estado estacionario o la velocidad a la cual las economías pobres crecen más que las ricas. Los resultados empíricos sobre la convergencia comparados con el resto de los países se pueden ver a continuación:
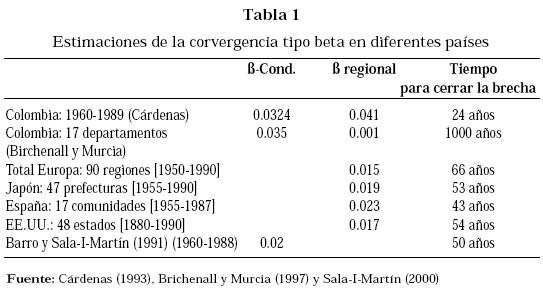
Como puede observarse en la Tabla 1, usando los cálculos de Cárdenas (1993) no cabe duda de que Colombia es un caso exitoso de convergencia regional por encima de Japón, Estados Unidos y España, pues mientras en Europa la velocidad de convergencia era del 1.5% anual, en Colombia la velocidad de convergencia era del 4% anual.1
Adicionalmente al concepto de convergencia tipo beta, β, se encuentra el concepto de convergencia tipo sigma, σ, el cual se relaciona con una menor dispersión del PIB en el tiempo proveniente de la menor distancia entre los países. De acuerdo con este criterio, es irrelevante si una economía presenta convergencia a un estado estacionario ya que el punto importante consiste en la evolución de la distribución de todos los países.2 La dispersión se calcula como la desviación estándar muestral. Si σ denota la desviación estándar de una sección cruzada de tamaño N, entonces:
De acuerdo con la ecuación 2, existe
una convergencia en el PIB si
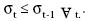 Es decir, existe una convergencia
tipo sigma si la desviación
estándar del logaritmo del PIB baja
a través del período de muestra.
Es decir, existe una convergencia
tipo sigma si la desviación
estándar del logaritmo del PIB baja
a través del período de muestra.
Cabe aclarar que las estimaciones de convergencia tipo beta y sigma de Barro y Sala-I-Martín (1992) y Mankiw, Romer y Weil (1992) se refieren a la convergencia condicional o relativa [Según Sala-I-Martín (1994)], que consiste en "medir" la distancia entre el nivel de renta de un país y su nivel de renta del estado estacionario condicionado sobre una serie de variables que actúan como proxi del estado estacionario.3 De esta forma se corrobora la convergencia tipo β si se encuentra una correlación parcial negativa entre el crecimiento y el nivel de renta condicional al estado estacionario. Esto último implica que "si efectuamos una regresión con datos de sección cruzada del crecimiento sobre la renta inicial, manteniendo constante un cierto número de variables adicionales (que actúan de proxi del estado estacionario) y, encontramos que el coeficiente de la renta inicial es negativo, entonces decimos que las economías en nuestro conjunto de datos presentan β- convergencia condicional" . Sala-I-Martín (2000, Pág. 139).
2. FALACIAS EN TORNO A LA HIPÓTESIS DE CONVERGENCIA
Muchos de los trabajos empíricos durante la década de los años noventa mostraron que las series de las que se querían extraer propiedades de convergencia no eran estacionarias sino que por el contrario tenían al menos una raíz unitaria. Lo cual implicaba que detrás del supuesto estado estable (resumido en β) existían procesos dinámicos mucho más complejos de lo que se había pensado y que no son incorporados en las ecuaciones de convergencia.
Quah (1996) muestra que detrás de la tasa de convergencia del 2% anual entre países puede encontrarse un proceso de raíz unitaria. Haciendo bT = e-βT, la ecuación 1 se puede reescribir como:
Si se multiplica por T la ecuación 3, β toma un valor de 0.02 (2% de convergencia) y T es igual a 10, entonces el valor de bT será de 0.82. Observe también que si β es igual a 0.02 (2% de convergencia) y T es igual a 1 entonces bT será igual a 0.98 cuyo valor es muy cercano a 1. Por lo tanto, detrás de una tasa de convergencia del 2% se puede estar ocultando un proceso de una raíz unitaria.
Con el fin de corroborar esta idea, Quah presenta simulaciones de corte transversal de la ecuación 3 con series de transversales generadas como paseos aleatorios independientes. Los resultados de β son:
De la Tabla 2 se puede observar que para 200 series generadas como paseos aleatorios con un período de 60 años si se realiza la regresión de 1 entonces el valor de β encontrado es similar al encontrado empíricamente en las regresiones de convergencia. De esta forma el valor de convergencia tipo β encontrado revelaría la existencia de series no estacionarias y, por lo tanto, la ecuación 1 se convertiría en una prueba de raíces unitarias (Pág. 1358).4
De la ecuación 2 se puede observar que la convergencia tipo sigma nos muestra cuando la dispersión entre países disminuye en el tiempo. Por lo tanto, si no es muy relevante el convergencia a un estado estacionario, entonces lo importante consistirá en la forma como evoluciona la distribución de todos los países.
De esta forma, lo importante cuando se muestra la convergencia tipo sigma consiste en el comportamiento de la distribución a través de los países. La relación entre ambas convergencias es clara: Supongamos que los Y´s son {i.i.d} a través de la sección transversal, entonces:
En la ecuación 4 µi(t) es {i.i.d} en el tiempo con varianza positiva y finita σ2 u, por lo tanto, elevando al cuadrado y tomando valores esperados:
La ecuación 5 muestra la relación entre ambas convergencias, pero también muestra que la convergencia tipo beta no implica la convergencia tipo sigma, pues la convergencia depende de cuando σ20>(1-b2)-1σ2u pues si esto se cumple σ2t cae monótonamente y si no crece, por lo tanto no habría convergencia. Sin embargo, aunque exista convergencia tipo sigma, esta puede provenir de dos mundos posibles:
Los gráficos 1 y 2 muestran una convergencia tipo sigma donde ésta permanece invariante. En la primera gráfica la convergencia sigma permanece constante alrededor de una banda mientras que el PIB fluctúa En la segunda gráfica, tanto el PIB como sigma permanecen constantes a lo largo del tiempo. Sin embargo, estas dos gráficas muestran dos mundos totalmente diferentes: uno donde se presenta el salto de rana(leap-froggin) y un mundo polarizado donde los países ricos siempre serán ricos y los países pobres siempre serán pobres.
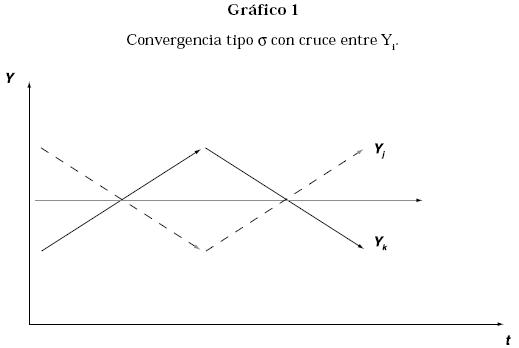

Por lo tanto, la convergencia tipo sigma no nos dice nada acerca de la distribución del PIB ni de la tan soñada convergencia. Esa es la principal crítica en Quah (1993), pues la regresión de corte transversal y la estimación posterior de la ecuación 2 puede representar solamente el comportamiento promedio y no la distribución.
En Quah (1993) se parte de discutir las propiedades dinámicas de la ecuación de convergencia usando la famosa falacia de Galton que ya había sido planteada por Hotelling en la crítica al trabajo de Secrist.
"(Secrist había trazado) promedio de grupos, arreglados de acuerdo con el valor de la variable en el primer año de la serie; si fueran arreglados de acuerdo con los valores tomados por la variable en el último año de la serie las líneas divergirían. La aparente convergencia es una falacia estadística resultante del método de agrupación. El verdadero test de una tendencia a la convergencia sería el mostrar una disminución consistente de la varianza, no entre medias de grupos, sino entre empresas individuales". Hotelling en Friedman (1992, página 2129).
Como muestra Quah (1993), en primer lugar la correlación negativa no es el resultado de que la distribución de los países cumpla con los criterios de convergencia, sino el cumplimiento de la Falacia de Galton originada por derivar implicaciones dinámicas del comportamiento estático de la distribución de los países en el tiempo, que se develaría si se analiza la distribución de los países a lo largo del tiempo.
3. CLUBES DE CONVERGENCIA
A continuación Quah propone la siguiente idea:
De esta forma pueden existir coaliciones o clubes de convergencia formados endógenamente a través de todos los países, y las dinámicas de convergencia diferentes dependerán de la distribución inicial de las características de los países. Estas dinámicas incluyen la polarización: los países ricos serán más ricos y los pobres más pobres y los de clase media desaparecerán. La estratificación: modas múltiples en la distribución de PIB de los países y dar alcance a economías que divergen [Quah (1993,1997)]. Lo cual se puede ver mejor en el siguiente gráfico:

En el Gráfico 3 las economías poseen una distribución inicial del PIB en t0 a través de los países. En el tiempo, algunas estarán mejores y otras peor. Las coaliciones o clubes de convergencia se forman, y la distribución tiende hacia una distribución bimodal en el tiempo t1. El número exacto de coaliciones y su composición depende de la distribución inicial del PIB y cuando el PIB de todos los países es similar entonces se tiende a una sola coalición y ocurre una convergencia a la igualdad. Por otro lado, si el PIB es desigual, entonces se pueden formar múltiples clubes de convergencia.
Esto es lo que no se puede explicar aplicando la metodología de la convergencia tipo beta, pues como muestra Quah, un investigador podría creer que entiende el comportamiento del PIB a través de una muestra de corte transversal entre países controlando por diferencias en los stocks de capital humano y otras variables. Sus resultados pueden indicarle que la convergencia condicional ocurre y que el capital humano explica los patrones de crecimiento entre países, sin embargo, estos resultados podrían estar errados ya que el capital humano respondería solamente a las estructuras de coaliciones formadas endógenamente y explicaría por qué un mayor capital humano se encuentra entre los países que pertenecen al club de los ricos.
Ahora bien, ¿qué muestran los datos? ¿Se comporta la distribución en forma unimodal? Si observamos, por ejemplo, la distribución del PIB en 1960, 1985 y luego en 20005 ¿qué encontraríamos? Veamos qué revela la distribución de países:6

Como se puede observar del Gráfico 4, la distribución del logaritmo del PIB en 1960 revela una distribución unimodal. En 1985 la distribución muestra la siguiente forma:
Para el año 2000 la distribución tiene la siguiente forma:

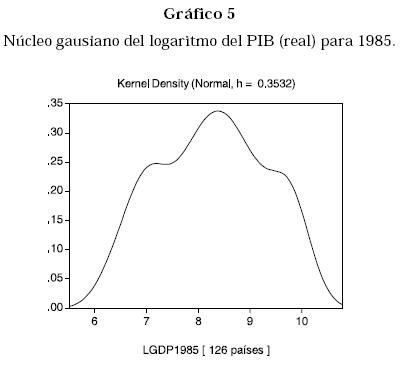
Como se puede observar en el Gráfico 5, la distribución en el año 1985 claramente no es unimodal y las cosas no parecen haber mejorado después como se puede observar del gráfico del núcleo gausiano para el año 2000, Gráfico 6. De esta forma, los Gráficos 5 y 6 se parecen más al Gráfico 3 en donde Quah muestra la existencia de Clubes de Convergencia.
Con el fin de contrastar la idea de que en el año 1960 la distribución era unimodal, mientras en 1985 y 2000 se aproxima más a una bimodal, se usa el test de Silverman (1986) de multimodalidad, cuyos resultados fueron:

Dado que el valor crítico para aceptar un determinado número de modas es de 0.4, entonces, de la Tabla 3 se acepta que en 1960 la distribución presenta una moda mientras en los años 1985 y 2000 la distribución presenta dos modas.7
De esta forma cualquier estimación de convergencia realizada por la metodología tradicional estará errada. Los gráficos 4 y 5 nos muestran un hecho interesante: La distribución del PIB transita del año 1960 al año 2000 a una distribución bimodal, pero ¿cómo se puede explicar el paso del Gráfico 4 al Gráfico 5 o al Gráfico 6?
Para explicar la transición de una distribución unimodal a una distribución bimodal Quah supone lo siguiente:
Sea Ft la distribución de PIB a través de los países en el período t. Asociado a tal distribución existe una medida λt. La evolución de Ft ó λt es una medida auto-regresiva de la siguiente forma:
En la ecuación 6 M es el núcleo estocástico: el mapeo del producto cartesiano de los valores del PIB y los conjuntos mensurables en el intervalo [0 , 1]. El núcleo M mapea una medida λt en otra λt-1, por lo tanto "M codifica la información sobre la dinámica intra-distribucional, si las economías como Corea y Filipinas, digamos, que estaban muy juntas en 1950, transitaron a niveles de ingreso diferentes. Esta, además, contiene por consiguiente estrictamente más información que sólo estadísticas agregadas como medias o desviaciones estándar" [Quah (1996b, pp. 1370)].
De acuerdo con Quah (1993, 1996b) la ecuación 6 es análoga a un AR(1), excepto en que los valores son distribuciones y no escalares o vectores de números y no contiene implícitamente innovaciones o perturbaciones. Reescribiendo 6:
Iterando la ecuación 7 se tiene:
Tomando límite cuando 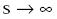 , en la
ecuación 8, se puede caracterizar el
comportamiento de largo plazo o la
distribución ergódica del PIB de los
países. La convergencia hacia la
igualdad puede manifestarse en un
punto degenerado, mientras que un
mundo expresado por el gráfico 3 ó 5
y 6 muestra la convergencia a una
medida bimodal. Los resultados encontrados
por Quah (1996b, 1993,
1997) son:
, en la
ecuación 8, se puede caracterizar el
comportamiento de largo plazo o la
distribución ergódica del PIB de los
países. La convergencia hacia la
igualdad puede manifestarse en un
punto degenerado, mientras que un
mundo expresado por el gráfico 3 ó 5
y 6 muestra la convergencia a una
medida bimodal. Los resultados encontrados
por Quah (1996b, 1993,
1997) son:

La Tabla 4 es una cadena markoviana donde el período de transición es de un año. La entrada número muestra el número total de observaciones: por ejemplo, en la fila 2 el valor de 643 observaciones se forma tomando 113 países a través de 23 años. Los valores de 1/4, 1/2, 1, 2 e infinito son valores tomados a partir del PIB y muestran los estados de la cadena markoviana. De esta forma los elementos de la diagonal son las probabilidades de permanecer en el mismo estado y los elementos diferentes de la diagonal la probabilidad de pasar de un estado a otro estado.
La forma de calcular la Tabla 4 no es clara en ninguno de los documentos de trabajo o los artículos de Quah, y es toda una incógnita cómo se llega a la matriz de Markov presentada por Quah: en el trabajo de (1996b) se remite al trabajo de Quah (1996a) y en Quah (1996a) se remite a Quah (1993) y en Quah (1993) coloca el mismo párrafo que en 1996a y 1993.8 Sala-IMartín (2000, 225) propone que lo que hace Quah es lo siguiente:
Una vez que se llega a la matriz de transiciones, Tabla 4, se calcula la matriz ergódica solucionando recursivamente la ecuación 8. Tomando los datos de la Tabla 4 se obtiene la siguiente matriz de transición:

Los resultados de la Tabla 5 son similares a los obtenidos por Quah y que aparecen en la última fila de la Tabla 4. Las diferencias existentes entre ambas tablas se deben a que mientras la matriz ergódica de la Tabla 5 fue calculada a partir de la Tabla 4, la matriz ergódica de la Tabla 5 no se deriva de la matriz de primer orden, sino de los datos usados por Quah, y dado que Quah coloca ceros en cada celda de la Tabla 4 cuando el valor tiene más de dos dígitos que comienzan cero, es natural que se presenten diferencias.
Ambos cálculos corroboran que las probabilidades se concentran en las colas extremas, mostrando de esta forma la existencia de clubes de convergencias en las colas altas y bajas del PIB mientras la clase media se desvanece [Quah (1996,1372)].
Sin embargo, la concentración en las colas no se debe a la aplicación de un núcleo estocástico como nos lo dice Quah, es consecuencia de aplicar las propiedades de las cadenas de Markov, como se puede observar de la Tabla 5.
CONCLUSIONES
El artículo de Quah es brillante en mostrar que las regresiones sobre la convergencia tipo beta podrían sólo ser pruebas de raíces unitarias y que un valor de β del 0.02% tan sólo corroboraría que la serie del PIB no es estacionaria. Es decir, que la tan famosa convergencia del 2% en el ámbito mundial encontrada en la ecuación 1 no es más que la revelación de que la serie es un proceso de raíz unitaria.
Cuando Quah discute la convergencia tipo sigma, sus resultados son igual de provocadores: La estabilidad de la misma podría alcanzarse en varios escenarios o mundos posibles: algunos con saltos entre bandas y otros donde existen clubes de convergencia o polarizaciones en el PIB.
Con respecto a su idea sobre la evolución del PIB es novedosa, pero oscura: Ninguno de sus trabajos muestra cómo se calcula M (ni en los artículos publicados ni en los documentos de trabajo), aunque el punto de partida es precisamente esta matriz.
En los artículos de 1993, 1996b y 1997 cuando Quah llega al cálculo de la matriz de primer orden usa palabras como el núcleo estocástico, etc., cuando se refiere a M. Sin embargo, es claro que las propiedades derivadas son las tradicionales de una cadena de Markov y que la solución a la ecuación 8 consiste en encontrar la distribución estacionaria de la cadena markoviana10 y no en la solución al núcleo estocástico.
Cuando se itera la ecuación 7 se puede observar que la distribución ergódica no es otra cosa que la matriz markoviana de largo plazo, ecuación 8. Los resultados de aplicar dichas propiedades, expresadas en la Tabla 5, muestran estimaciones similares para el largo plazo: concentración en las colas. De esta forma la estimación del núcleo estocástico es bastante discutible y, por lo tanto, la transición entre países queda reducida a una cadena de Markov de un paso.
Sin embargo, aunque los resultados sobre el núcleo estocástico sean bastante discutibles, no cabe duda de que el impacto del trabajo de Quah sobre la convergencia y, en últimas, sobre los trabajos de Barro y Sala-I-Martín fue demoledor. La idea de los clubes de convergencia es irrebatible cuando se observan las distribuciones entre 1962, 1985 y 2000 y se comprueba que la distribución del PIB sigue siendo bimodal en 2000. Muchos intentos se han hecho por minimizar el embate de Quah, uno de los más importantes ha sido el de Jones (1997) [Citado con énfasis por Sala-I-Martín (2000)], quien después de calcular la matriz M muestra que el porcentaje de países ricos aumentará en el largo plazo y el de pobres disminuirá, en el supuesto de las economías crecerán más rápido de lo que decrecen. Pero los resultados del trabajo de Jones (1997) también son discutibles, ya que la información recogida en la matriz inicial M debe permanecer hasta el período de simulación t, pues de lo contrario no se podría encontrar la distribución ergódica. Esto implica imponer las condiciones de evolución de los países entre 1962 y 1985 sobre el resto de períodos, una restricción bastante discutible tanto para Jones como para Quah.
NOTAS AL PIE DE PÁGINA
1. Lo cual implica que si las condiciones se mantienen la disparidad entre regiones necesita un período de diecinueve años para cerrar la brecha entre las regiones (0.052*19.2 ≈1). Los trabajos de Meisel (1993), Rocha y Vivas (1998), Birchenall y Murcia (1997) y Bonet y Meisel (2001) muestran que para el período analizado por Cárdenas (1993) no existió convergencia entre las regiones en Colombia.
2. Sin embargo, como aclara Sala-I-Martín (2000, 196), la convergencia tipo beta es una condición necesaria para la existencia de la convergencia tipo sigma, pero no es una condición suficiente.
3. Las primeras estimaciones de la ecuación 1 mostraron que no existía convergencia de acuerdo con los resultados presentados por Summers, A y Heston, R (1991). Estos resultados, que mostraban una victoria de los modelos de crecimiento endógeno y una derrota del modelo neoclásico fue lo que llevó a la contra-revolución establecida por Barro y Sala-I-Martín (1992a,b).
4. Con respecto al PIB de los Estados Unidos Nelson y Plosser (1982) y Perron (1989) mostraron la existencia de una raíz unitaria en esta serie. En Colombia, Posada (1993) y Mora y Salazar (1994), entre otros, muestran la existencia de una raíz unitaria y Mora (1997) muestra la existencia de no-linealidades en el PIB de Colombia. Estos resultados empíricos, presentes en muchas de las series del PIB de los países en el mundo, corroboran lo inadecuado de la regresión de corte transversal.
5. El período 1962 - 1985 es el que se ha usado en la gran parte de los trabajos sobre convergencia condicional y es el que usa Quah; se analiza adicionalmente el año 2000 para ver qué tanto ha cambiado la distribución. Los datos son tomados del Penn World de Summers y Heston (1993) del PIB per cápita real de acuerdo con el índice de Laspeyres.
6. El núcleo de Epanechnikov es más eficiente que el núcleo gausiano, se usó el núcleo gausiano debido a que el test de Silverman para multimodalidad en STATA usa el núcleo gausiano. De otro lado, la banda usada en E-Views difiere del valor crítico en STATA debido a que las rutinas usadas por silverman.ado implica bandas fijas.
7. La prueba de Silverman se desarrolla en STATA con las rutinas warpdenm.ado y silvtest.ado desarrolladas por Isaías H. Salgado-Ugarte, Makoto Shimizu y Toru Taniuchi.
8. En el documento de trabajo de 1993 Quah menciona que todos sus cálculos se realizaron en el paquete econométrico tSrF que funciona sólo bajo Linux.
10. Siguiendo a Quah (1993) sea Ft+1 = M Ft donde M tiene las propiedades descritas anteriormente, entonces esta ecuación “Is like a estándar firts order autorregresion, except its values are distributions (rather scalars or vectors of nambers), and it contains no explicit disturbance or innovation”, pág (429).
BIBLIOGRAFÍA
Cárdenas, M. (1993) "Crecimiento y convergencia en Colombia: 1950-1990" , Revista Planeación y Desarrollo, diciembre, edición especial.
Cohen, D. (1995) "Test of the Convergence Hypothesis: Some Further Results" , CEPR Working Paper 1163.
Barro R.J. y Sala-I-Martin, X. (1992a) Economic Growth, New York: McGraw-Hill.
Barro R.J. y Sala-I-Martin, X. (1992b), "Convergence" , Journal of Political Economy, vol. 100, No. 2, 223- 251.
Birchenall, J. y Murcia G. (1997) "Convergencia regional: una revisión del caso colombiano". Desarrollo y Sociedad, No. 40.
Bonet, J. y Meisel, A. (2001) "La convergencia regional en Colombia: una visión de largo plazo, 1926-1995". En Regiones, ciudades y crecimiento económico en Colombia, A. Meisel (editor), Colección de Economía Regional, Banco de la República.
Friedman, M. (1992) "Do Old Fallacies Ever Die", Journal of Economic Literature, vol. 30, No. 2, 2129-2132.
Jones, Ch. I. (1997) "On the Evolution of the World Income Distribution", Journal of Economics Perspectives, vol. 11, No. 3, 19-36.
Mora, J.J. y Salazar, B. (1994) "Fábula y trama en el relato de la convergencia", Boletín Socioeconomico, Universidad del Valle. No. 27, pp.99-116.
Mora, J.J. y Salazar, B. (1997) "No-linealidades y ciclos asimétricos en el PIB colombiano", Estudios Económicos, Vol 12, Núm. 2, pp.183-195.
Murcia, G. (1997) "Convergencia departamental en Colombia". S.L.: DNP-UMACRO.
Nelson, Ch.R y Plosser, Ch.I. (1982) "Trends and Random Walks in Macroeconomics Time Series: Some evidence and Implications", Journal of Monetary Economics, núm. 10, pp. 139-162.
Meisel, A. (1993) "¿Polarización o convergencia? A propósito de Cárdenas, Pontón y Trujillo", Coyuntura Económica, Vol. 23. No. 2.
McCloskey, D. (1994) "1780-1860: A Survey". In: R. Floud, D. Mc- Closkey, eds., The Economic History of Britain Since 1700, vol. 1, Cambridge: Cambridge University Press 1994, pp. 242-71.
Mankiw, G., Romer, D. y Weil, N. (1992) "A Contribution to the Empirics of Economic Growth", Quarterly Journal of Economics, vol. 107, 407-413.
Posada, C.E. (1993) "Productividad, crecimiento y ciclos", Banca y Finanzas, núm. 29, pp.59-95.
Perron, P. (1989) "The Great Crash, the Oil Shock and the Unit Root Hypothesis" , Econometrica, núm. 57, pp. 1361-1401.
Quah, D. (1993) "Galton´s Fallacy and Tests of the Convergence Hypothesis", W.P. Department of Economics L.S.E (1993); Scandinavian Journal of Economics, Diciembre 1993 (Reimpreso en T.M. Andersen and K.O. Moene (eds.), Endogenous Growth, Blackwell, 1993).
Quah, D. (1996) "Empirics for Economic Growth and Convergence", European Economic Review, vol. 40, No. 6, 1353- 1375.
Quah, D. (1996) "Twin Peaks: Growth and Convergence in Models of Distribution Dynamics", The Economic Journal, vol. 106, 1045-1055.
Quah, D. (1997) "Empirics for Growth and Convergence: Stratification, Polarization, and Convergence Clubs", Journal of Economic Growth, vol 2. No. 1, 27-60.
Rocha, R. y Vivas, A. (1998) "Crecimiento regional en Colombia: ¿persiste la desigualdad?", Revista de Economía del Rosario, Vol. 1, No. 1.
Sala-I-Martín, X. (2000) Apuntes de crecimiento económico. Barcelona: Antoni Bosh editor.
Silverman, B.W. (1986). Density Estimation for Statistics and Data Analysis. Londres: Chapman and Hall.
Summers, A y Heston, R (1991) "The Penn World Table(Mark 5): An expanded set of international comparations, 1950-1988", Quarterly Journal of Economics, vol. 106, no. 2, 327, 368. en http://www.chass.utoronto.ca/ (2002) y Penn World Table 6.1