
HERRAMIENTA DE ANÁLISIS MULTI-CRITERIO COMO SOPORTE PARA EL DISEÑO DEL PROGRAMA SOCIAL DE LA FACULTAD DE INGENIERÍA1
SANDRA LORENA GALARZA MOLINA, Ing.*1, ANDRÉS TORRES, Ing.2, SANDRA MÉNDEZ FAJARDO, Ing.3, BLANCA CECILIA PÉREZ MUZUZU, Ms.4
1Estudiante de Doctorado en Ingeniería, Pontificia Universidad Javeriana, CeiBA-Complejidad, Colombia. sgalarza@javeriana.edu.co
2Profesor Asociado, Director Grupo de Investigación Ciencia e Ingeniería del Agua y el Ambiente, Pontificia Universidad Javeriana, Colombia. andres.torres@javeriana.edu.co
3Profesora Asistente, Coordinadora Proyecto Social de la Facultad de Ingeniería PROSOFI, Pontificia Universidad Javeriana, Colombia. sandra.mendez@javeriana.edu.co
4Coordinadora Proyección Social - Facultad de Ingeniería, Pontificia Universidad Javeriana, Colombia. bc.perez@javeriana.edu.co
*Autor para correspondencia. Enviar correspondencia a: Departamento de Ingeniería Civil - Facultad de Ingeniería - Calle 40 No. 5-50, Edif. José Gabriel Maldonado, S.J. Bogotá D.C., Colombia.
Fecha de recepción: 06-08-2010 Fecha de corrección: 10-12-2010 Fecha de aceptación: 03-10-2011
RESUMEN
El objetivo de esta investigación es desarrollar una herramienta para el Análisis Multi-Criterio como soporte para la selección de la comunidad objetivo del Programa Social de la Facultad de Ingeniería (PROSOFI) de la Pontificia Universidad Javeriana de Bogotá (Colombia). Esta herramienta utiliza el Análisis Multi-Criterio (AMC), el cual se basa en modelos de decisión que contienen diferentes posibles soluciones. Para la evaluación de cada una de las alternativas (diecinueve localidades y dos municipios) se propusieron siete criterios: ubicación geográfica, presencia previa en la comunidad, necesidades básicas insatisfechas, apoyo de instituciones, marginalidad, organizaciones sociales y elementos culturales. Las alternativas y los factores de ponderación se definieron a partir de un trabajo participativo de la Facultad. Los resultados indican que las comunidades con mayor opción son Usme y Ciudad Bolívar.
PALABRAS CLAVE
Toma de decisiones, Análisis Multi-Criterio, ELECTRE II.
Clasificación JEL: D70
ABSTRACT
A multi-criteria analysis tool as support for selecting the target community for the social outreach program of the School of Engineering
This document aims to develop a multi-criteria analysis tool as support for the selection of the target community of the social outreach program (PROSOFI, because of its Spanish acronym) of the School of Engineering at Pontificia Universidad Javeriana in Bogotá (PUJB). This tool uses multi-criteria analysis (MCA) based on decision models that provide different possible solutions. For evaluating each of the multiple alternatives (19 urban districts and 2 towns), seven criteria were proposed, including, location, marginality, and unsatisfied basic needs, among others. Both alternatives and weighting factors were defined based on the participatory work of the School. The results show that communities which are most likely to be selected are Usme and Ciudad Bolivar.
KEYWORDS
Multiple criteria analysis, decision making, ELECTRE II.
RESUMO
Ferramenta de análise multi critério como suporte para o projeto do programa social da Faculdade de Engenharia
O objetivo desta pesquisa é desenvolver uma ferramenta para a Análise Multi Critério como apoio para a seleção da comunidade alvo do Programa de Social da Faculdade de Engenharia (PROSOFI) da Pontificia Universidad Javeriana de Bogotá (Colômbia). Esta ferramenta utiliza a Análise Multi Critério (AMC), a qual se baseia em modelos de decisão contendo diferentes soluções possíveis. Para a avaliação de cada uma das alternativas (dezenove cidades e dois municípios) foram propostos sete critérios: localização geográfica, presença prévia na comunidade, necessidades básicas não atendidas, apoio de instituições, marginalidade, organizacional social e elementos culturais. As alternativas e os fatores de ponderação foram definidos a partir de um trabalho participativo da Faculdade. Os resultados indicam que as comunidades com mais opções são Usme e Ciudad Bolívar.
PALAVRAS CHAVE
Tomada de decisões, Análise Multi Critério, ELECTRE II.
INTRODUCCIÓN
La toma de decisiones en grupo es una actividad frecuente e importante en las organizaciones. Obtener herramientas, como el uso de modelos explícitos pero no necesariamente formalizados, ayudará a los involucrados en la toma de decisiones a responder las preguntas que surgen durante este proceso. Estas herramientas ayudan a ilustrar las posibles soluciones y a generar una recomendación que aumente la coherencia entre la evolución del proceso y los objetivos de las partes interesadas. La palabra recomendación se utiliza para que tanto el analista como la persona o el grupo de personas que toman la decisión estén enterados que están en libertad de seguir o no las sugerencias (Roy, 2005).
Cuando se busca una toma de decisiones grupal lo ideal es obtener un consenso para lograr unidad y apropiación, y así evitar una simple votación (Ben-Arieh y Chen, 2006). Obtener lo anterior usualmente requiere de grandes esfuerzos por parte de las organizaciones y puede generar desgastes importantes del grupo decisor (Doumpos y Zopounidis, 2004). Adicionalmente, muchas de las decisiones que afectan directamente a un grupo de personas involucran el examen de un conjunto de posibles alternativas a través de un conjunto de criterios, para lo cual es necesario que el grupo decisor cuente con herramientas que los lleve a tomar la decisión más adecuada (Doumpos y Zopounidis, 1998). Pero, ¿cómo lograr que la toma de decisiones tenga un carácter más racional y menos emocional? ¿cómo lograr consenso sin generar desgaste?
A nivel internacional, a partir de los años sesenta, se han desarrollado las técnicas de Análisis Multi-Criterio (AMC en adelante) para dar soporte a la toma de decisiones (Roy, 1968). Desde entonces, dichas técnicas han sido objeto de numerosas investigaciones en diversos campos como la medicina, la ingeniería, las finanzas y la economía (Araújo, Rogério y Dantas, 2007; Belacel, 2000; Chen y Hung, 2009; Doumpos y Zopounidis, 1998; Hajkowicz y Collins, 2006; Uzoka, Osuji y Obot, 2011).
El AMC compara las alternativas, las cuales pueden ser cualitativas o cuantitativas, por medio de puntuaciones de éstas frente a diferentes criterios (Belacel, 2000; Smith, Mesa, Dyner, Jaramillo, Poveda y Valencia, 2000). Diversos autores (Ben-Arieh y Chen, 2006; Carlsson y Fuller, 2000; Delgado, Herrera, Herrera-Viedma y Martinez, 1998; Weinhardt y Seifert, 2010; Xu, 2005) se han concentrado en la inclusión de etiquetas lingüísticas para la toma de decisiones mediante la evaluación de las alternativas de forma cualitativa, dado que con frecuencia, para los expertos, resulta difícil expresar las preferencias mediante números exactos.
Por otra parte, para la fase de evaluación de los proyectos, generalmente se utilizan métodos que articulan la estructura de preferencia del decisor como los métodos de clasificación, por ejemplo, ELECTRE II. Sin embargo, el análisis del uso de estos tipos de sistemas demuestra que es preferible el desarrollo de herramientas específicas. Esta evidencia podría generalizarse para cualquier fase de los proyectos que involucra la toma de decisiones (Baptista, Barraud, Alfakih, Nascimento, Fernandes, Moura y Castro, 2004). Por consiguiente, se hace necesario el desarrollo de una herramienta específica para la toma de decisiones, teniendo en cuenta múltiples criterios e involucrando a los diferentes actores implicados (múltiples objetivos).
La Facultad de Ingeniería de la Pontificia Universidad Javeriana, sede Bogotá (PUJB), requiere diseñar el Programa Social de la Facultad de Ingeniería (PROSOFI). Este programa nace de la idea de unificar esfuerzos de docencia, investigación y servicio de las cuatro disciplinas (civil, industrial, electrónica y sistemas) para concentrarlos solo un territorio. La escogencia de dicho territorio representa una toma de decisión que involucra múltiples criterios. Adicionalmente, los decisores se ven enfrentados a las siguientes preguntas: ¿cómo escoger la comunidad y con qué criterios? ¿todos los actores involucrados tienen las mismas prioridades?
Debido a la variabilidad de los criterios, la cantidad de posibles comunidades objetivo y la diversidad de los actores involucrados, tomar una decisión de manera objetiva resulta complejo. Esta dificultad hace necesario utilizar una metodología que evalúe cada posible opción e incorpore estructura, transparencia, capacidad de auditoría y rigor a las decisiones (Hajkowicz y Higgins, 2006).
El presente artículo pretende describir la metodología que se ha planteado para hacer más efectiva la toma de decisiones en la selección de la comunidad objetivo para llevar a cabo PROSOFI.
Este artículo se organiza de la siguiente manera. La primera sección presenta la herramienta AMC seleccionada y la descripción de la zona de estudio. La segunda sección describe la herramienta computacional desarrollada para la selección de la comunidad objetivo. En la tercera sección se presentan y discuten los resultados obtenidos aplicando las técnicas de AMC, descritas mediante la ejecución de la herramienta computacional presentada en la segunda sección. Finalmente, en la cuarta sección se muestran las conclusiones y recomendaciones que orientarán el desarrollo de futuras investigaciones sobre técnicas de AMC.
1. MATERIALES Y MÉTODOS
Para el presente trabajo se escogieron las siguientes metodologías: (i) el método ELECTRE II, el cual hace parte de los métodos de relaciones de superación o clasificación, y (ii) el Método de la Suma Ponderada, el cual hace parte de los métodos que se basan en utilidades o valores. Adicionalmente, en esta sección se describe la zona de estudio.
1.1. Técnicas de análisis Multicriterio (AMC)
Debido a que las decisiones se basan en diferentes criterios, se ha desarrollado el Análisis Multi-Criterio (AMC), el cual se soporta en modelos de decisión que contienen diferentes posibles soluciones. Esas soluciones requieren ser evaluadas o clasificadas por la persona o el grupo de personas que toman la decisión, según diferentes criterios que generalmente son evaluados en distintas unidades. Existe una gran diversidad de términos para referirse al AMC como son: Soporte a la Decisión con Múltiples Objetivos (SDMO), Atributos Múltiples para la Toma de Decisiones (AMTD) y Análisis Multi-Criterio de Decisión (AMCD) (Hajkowicz y Collins, 2006).
Generalmente, al enfrentarse con un problema en la toma de decisión, se pueden efectuar cuatro tipos de análisis (Roy, 1968): (i) identificar la mejor alternativa o seleccionar un grupo con las mejores alternativas, (ii) determinar el orden (ranquin) de la mejor a la peor de las alternativas, (iii) clasificar las alternativas en grupos homogéneos predefinidos, y (iv) identificar las principales características de diferencia de las alternativas y describirlas con base en estas características.
A su vez, varios autores (Howard, 1991; RAC, 1992) han explicado el proceso del AMC, el cual contiene las fases descritas en la Tabla 1 (Hajkowicz y Higgins, 2006).

En general, este proceso es iterativo, dejando la posibilidad de abordar varias veces cualquier etapa a medida que se desarrolla el análisis. Adicionalmente, es conveniente seleccionar varias alternativas de AMC de diferentes tipos de análisis para comparar los resultados obtenidos por diversas metodologías (Smith et al., 2000).
1.2. Método ELECTRE II
A finales de los años sesenta surgió el método ELECTRE II, el cual fue desarrollado por Roy (1968, 1971) y Roy y Bertier (1971). Este fue el primer método de la familia de ELECTRE especialmente diseñado para tratar los problemas de determinación del orden de las opciones (ranquin). A su vez, también fue el primer método que se basó en la construcción de secuencias de relaciones de superación binarias (Figueira, Mousseau y Roy, 2005).
Este método consiste en realizar comparaciones entre parejas de alternativas –posibles soluciones–, para lo cual es necesario establecer criterios de evaluación. Dichas comparaciones se basan en la matriz de posibles soluciones en la que cada alternativa se evalúa con respecto a cada criterio. Luego se pondera la importancia relativa de cada criterio en el conjunto, teniendo claridad sobre el sentido de preferencia de los criterios en la matriz de posibles soluciones (Roy, 1967).
Para comparar el desempeño de cada alternativa a y b se deben calcular los índices de concordancia y discordancia (Smith et al., 2000). El índice de concordancia entre a y b se define por medio de la Ecuación 1 (Figueira et al., 2005).
Donde c(a,b) es la suma de los pesos de aquellos criterios para los cuales la alternativa a es más deseable que la alternativa b.
El índice de discordancia se determina por medio de la Ecuación 2 (Figueira et al., 2005).
Donde d(a,b) es la diferencia máxima entre las puntuaciones asignadas a las alternativas (gj(b) y gj(a)) respecto a los criterios para los que la alternativa a no es más deseable que la alternativa b, dividida por el rango observado δj de cada criterio j y donde δj = max (gj(a), gj(b), ...,gj(n)) – min gj(a), gj(b), ...,gj(n)) y el juego de alternativas contempladas es {a, b,…, n} (Smith et al., 2000).
Ambos índices deben calcularse para cada una de las parejas de soluciones (a,b), donde a ≠ b. Con estos valores se construyen las matrices de concordancia C y de discordancia D, donde el elemento c(a,b) o d(a,b) representa el índice de concordancia o discordancia respectivamente entre las alternativas a y b, ubicado en la posición (a,b) de la matriz (ver Tabla 2) (Figueira et al., 2005).

Para definir las relaciones binarias, se estipulan tres niveles de concordancia (Cmin,i con i=1, 2,3 tal que Cmin,1≥ Cmin,2≥ Cmin,3≥0) y dos niveles aceptables de discordancia por criterio (dmax,i con i=1, 2,3 tal que 0≤dmax,1≤ dmax,2≤1) (Roy y Bertier, 1971).
Por lo tanto, una alternativa a es estrictamente preferida a la alternativa b si y sólo si una (o ambas) de las siguientes condiciones se cumplen (Roy y Bertier, 1971):
Condición 1 (Ecuaciones 3 y 4):
Condición 2 (Ecuaciones 5 y 6):
Para el caso de la superación débil, una alternativa a supera débilmente a b si y sólo si se cumple lo siguiente (Ecuaciones 7 y 8):
Una alternativa puede superar fuertemente o débilmente a otra. La superación fuerte indica una clara preferencia de una alternativa frente a la otra, mientras que la superación débil indica que no se puede asegurar de manera definitiva que una alternativa sea preferible a otra. La utilización de estos dos conceptos posibilita la clasificación de alternativas (Roy y Bertier, 1971).
Con las relaciones de superación entre las alternativas definidas se procede a representar el grafo débil y el grafo fuerte (ver Gráfico 1) (Roy, 1974; Roy y Bertier, 1971). Cada nodo del grafo representa una alternativa. En el caso del grafo fuerte, se muestra cuál alternativa supera fuertemente a otra (ver Gráfico 1a) y en el caso del grafo débil, se muestra cuál alternativa supera débilmente a otra (ver Gráfico 1b).
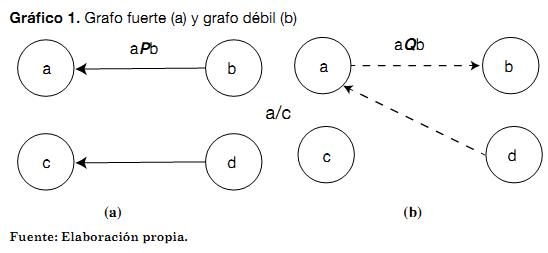
Con los grafos (débil y fuerte) definidos, continúa el procedimiento de clasificación, el cual se desarrolla en tres niveles. Inicialmente, se obtiene una clasificación directa, luego una indirecta y, finalmente, se promedian las dos clasificaciones anteriores generando la clasificación final (Smith et al., 2000).
A partir del grafo de relaciones se realiza la clasificación directa por medio del procedimiento descrito en la Tabla 3 y el algoritmo presentado en el Gráfico 3 (Smith et al., 2000). Donde k es el número de iteraciones, Y(k) es un subconjunto del grafo fuerte (Gf), Y(0) = Gf, y D, F, B y A(k) son conjuntos que se definen de la siguiente manera (Smith et al., 2000):


D Puntos sin antecedentes en el grafo fuerte (Gf)
F Puntos en que están ligados en el grafo débil (Gd)
B Puntos sin antecedentes en F, que no tienen precedentes en Gd
A(k) = (D – F)UB Son los puntos retenidos v' (A)
v' (A) Clasificación que se va asignando a cada A que pertenece a A(k).
El algoritmo finaliza cuando Y(k+1) es un conjunto vacío, por lo tanto todas las alternativas han sido clasificadas (Smith et al., 2000). Por otro lado, la clasificación indirecta consta de tres pasos descritos en la Tabla 4 (Smith et al., 2000).

1.3. Método de Suma Ponderada
Como existen diversas metodologías para la toma de decisiones, al momento de aplicar cualquiera de éstas se recomienda el uso de dos o más metodologías complementarias para validar o dar mayor claridad al proceso. Por lo anterior, se decidió la utilización del Método de la Suma Ponderada (Smith et al., 2000).
Este método parte de la matriz de posibles soluciones y consiste en determinar la evaluación global de cada alternativa (U(a), U(b), U(c),…) para luego comparar resultados y escoger aquella alternativa con mejor puntaje. Esta evaluación global se desarrolla de la siguiente manera:
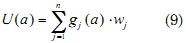
2. ZONA DE ESTUDIO
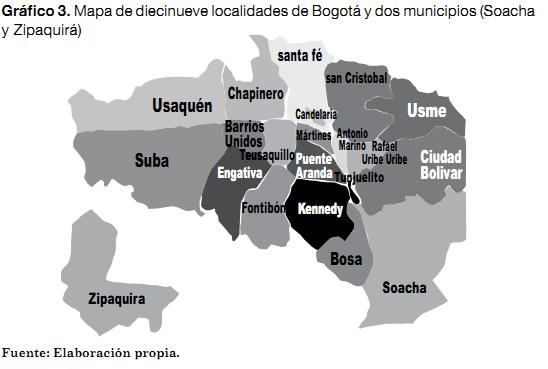
En el marco de este proyecto se recolectó información de diecinueve localidades de Bogotá (Antonio Nariño, Barrios Unidos, Bosa, Candelaria, Chapinero, Ciudad Bolívar, Engativá, Fontibón, Kennedy, Mártires, Puente Aranda, Rafael Uribe, San Cristóbal, Santafé, Suba, Teusaquillo, Tunjuelito, Usaquén y Usme) y dos municipios de Cundinamarca cercanos a Bogotá (Soacha y Zipaquirá) (ver Gráfico 3). Estas alternativas se pre-seleccionaron a partir de las experiencias previas de los programas sociales de: (i) la Facultad de Ingeniería, (ii) la Universidad Javeriana y (iii) la Compañía de Jesús. Únicamente se tuvieron en cuenta lugares dentro de Cundinamarca para facilitar la operatividad y manejo de recursos, y para que las personas de la comunidad elegida pudieran acercarse fácilmente a la PUJB, en caso de ser necesario.
Para definir los criterios y los pesos para evaluar las alternativas, se realizó una encuesta a 143 personas de la Facultad, la cual fue respondida por 111 individuos entre directivos, profesores y personal administrativo.
Adicionalmente, se consultó la opinión a doce expertos externos a la Facultad, entre los cuales se contó con líderes de proyectos sociales, teólogos, antropólogos, sociólogos, Sacerdotes Jesuitas, entre otros. En la encuesta se preguntaba cuáles criterios se debían considerar y cuáles eran los más importantes para escoger la comunidad. La encuesta fue respondida por nueves personas y para la ponderación de los pesos de los criterios, se le asignó una importancia de 70% a las respuestas de los funcionarios de la Facultad de Ingeniería y el 30% restante a la opinión de los expertos externos.
3. DESARROLLO DE LA HERRAMIENTA
Con las metodologías de AMC descritas anteriormente (ELECTRE II y el Método de la Suma Ponderada), se desarrolló un programa llamado CRIDE2 (herramienta de análisis multi-Criterio para la toma de DEcisiones) en MatLab®. Esta herramienta utiliza cuatro subrutinas llamadas GRAFOS, SACAR, CLASIFIC y PONDERA.
La primera subrutina utilizada es GRAFOS, la cual define los grafos débil y fuerte a partir de la matriz de soluciones y los umbrales de concordancia y discordancia. Tanto la matriz de soluciones como el umbral de concordancia son datos de entrada. Por otro lado, los umbrales de discordancia (dos por criterio) se determinan por medio de las máximas diferencias entre las alternativas de cada criterio: percentil 20 para el primer umbral (dmax,1) y percentil 35 para el segundo umbral (dmax,2).
Después de definir los grafos continúa el proceso con la clasificación directa (en la rutina principal CRIDE) e indirecta. Dentro de estos dos procesos se utiliza la subrutina SACAR, la cual se encarga de ir extrayendo de los grafos cada una de las alternativas evaluadas. De estos dos procesos se obtienen dos matrices Akdir y Akind, en las cuales cada fila equivale a la posición de clasificación.
Con las dos matrices de posición de clasificación (Akdir y Akind) se inicia el proceso de ponderaciones de las clasificaciones para obtener la clasificación definitiva, esto se hace a través de la subrutina CLASIFIC.
A continuación, con la subrutina PONDERA se determina la evaluación global de cada alternativa por medio del Método de la Suma Ponderada y, mediante el mejor puntaje, se obtiene la preferida. Para finalizar, se comparan los resultados obtenidos por las subrutinas CLASIFIC y PONDERA.
4. RESULTADOS Y DISCUSIÓN
Para dar soporte al proceso de toma de decisiones del Programa Social de la Facultad de Ingeniería (PROSOFI), se utilizaron las herramientas propuestas en el apartado 1. Inicialmente, como resultado de la encuesta, se obtuvo que se debían considerar los siguientes criterios: necesidades básicas insatisfechas, nivel de vulnerabilidad y marginalidad, dinámica y organización social, ubicación geográfica, presencia previa en la comunidad, apoyo de instituciones públicas o privadas, elementos culturales y étnicos.
En la Tabla 5 se muestran los criterios seleccionados con sus respectivos indicadores (17 en total). Adicionalmente, se obtuvieron los pesos para cada uno de los criterios definidos (ver Gráfico 4), los cuales indican la importancia que tiene un criterio respecto al otro.
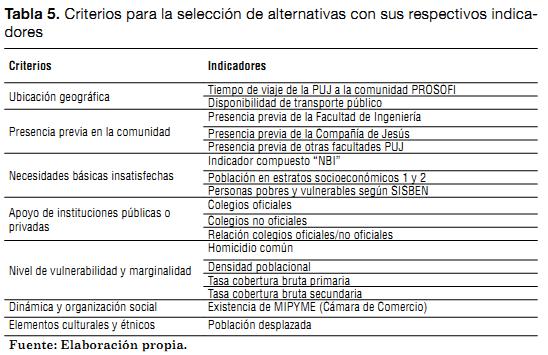
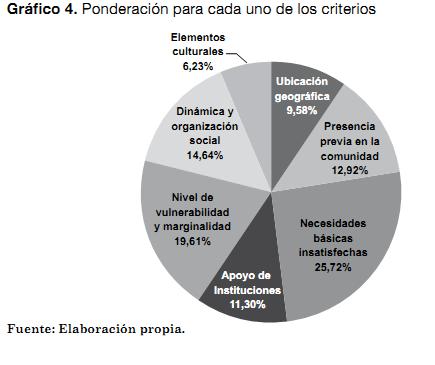
Se determinó el desempeño de las alternativas en cada uno de los criterios, obteniendo como resultado la matriz de posibles soluciones (ver Anexo 1). Esta matriz fue alimentada del último censo realizado en Bogotá (DANE, 2005), de información de la Cámara de Comercio de Bogotá (Cámara de Comercio de Bogotá, 2009), de la Subsecretaría de Planeación Socioeconómica (Subsecretaría de Planeación Socioeconómica, 2007) y de la experiencia de los expertos.
Con la matriz de posibles soluciones, las ponderaciones de los criterios y los sentidos de preferencia definidos, se pasó a la siguiente fase del AMC que consistió en determinar el orden de las alternativas utilizando CRIDE, la herramienta desarrollada.
Se realizaron tres ejecuciones del programa, las cuales se resumen en la Tabla 6. Los resultados se pueden observar en la Tabla 7, en la que sólo se presentan las localidades clasificadas en los primeros cinco puestos.


La primera ejecución de CRIDE respeta todos los criterios que se fijaron con el grupo de decisores y participantes en la encuesta, pero se vio la necesidad de hacer una segunda y tercera ejecución porque al llenar la matriz de desempeños, la evaluación de cada alternativa para algunos indicadores no era lo suficientemente objetiva ni realista. Debido a lo anterior, se eliminaron los indicadores "Dinámica y organización social - existencia de MIPYME", "Apoyo de instituciones públicas o privadas - colegios oficiales" y "Apoyo de instituciones públicas o privadas - colegios no oficiales".
El desempeño del indicador "Existencia de MIPYME" se obtuvo por medio de la Cámara de Comercio de Bogotá, entidad que registra la conformación legal de empresas. Es posible que estos datos oficiales no reflejen de manera fiel la dinámica y organización social de las poblaciones vulnerables porque, aunque hay empresas en funcionamiento en estas localidades, éstas no necesariamente están inscritas formalmente. Se consideró, por lo tanto, que al usar este indicador algunas localidades podrían estar en desventaja, especialmente las que cuentan con un mayor número de necesidades básicas insatisfechas.
Respecto a los indicadores "Apoyo de instituciones públicas o privadas – colegios oficiales y no oficiales", se consideró que un mayor número de colegios privados no implica necesariamente que la población tenga apoyo efectivo del sector privado, por el contrario, esto podría ser resultado de un mayor asistencialismo producto de coyunturas políticas o de otra índole. De igual manera, un mayor número de colegios públicos no indica con suficiencia la presencia del sector público en el territorio. Existen varias justificaciones para esta afirmación: en primer lugar, la educación no es la única línea de acción que se espera de un gobierno local para apoyar una población (se esperan además estrategias de salud, de cultura, deporte, saneamiento, etc.); y, en segundo lugar, para poder comparar entre localidades se tendría que relativizar, dividiendo por número de habitantes o número de familias.
Los resultados de la aplicación del Método de la Suma Ponderada se muestran en la Tabla 8. Como se puede observar, en los resultados arrojados por este método no se obtuvieron empates para las alternativas consideradas; por lo tanto, se estima que el Método de la Suma Ponderada es un buen método de apoyo al método ELECTRE II, en los casos que surjan empates. Se decidió integrar los dos métodos considerados (ELECTRE II y Método de la Suma Ponderada) en la herramienta CRIDE y los resultados definitivos se ilustran en la Tabla 9.
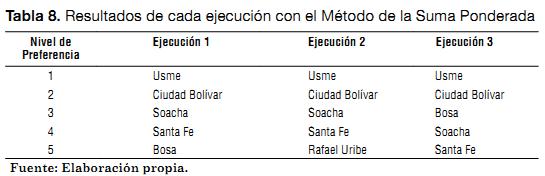
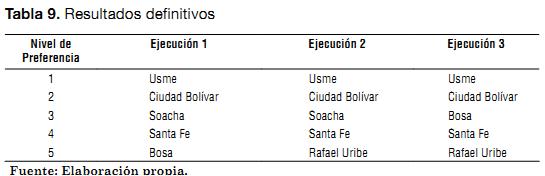
Respecto a las ejecuciones, se consideró que el mejor resultado de las tres es el tercero porque otorga un panorama más objetivo y realista. De igual forma, para escoger la comunidad específica, la segunda fase del diseño de PROSOFI, se elegirán las dos localidades que quedaron en los primeros dos puestos en cada ejecución mediante la utilización de CRIDE, a saber, Usme y Ciudad Bolívar.
5. CONCLUSIONES Y RECOMENDACIONES
Al utilizar CRIDE como base para el diseño de PROSOFI, se generó participación dentro de la Facultad de Ingeniería al consultar a los funcionarios y a los expertos sobre cuáles criterios se deberían utilizar para escoger la comunidad y con qué importancia. Este ejercicio logró una amplia participación e interacción entre personas con diferentes perfiles y formaciones (investigadores, docentes, trabajadores sociales, administrativos, etc.). Adicionalmente, se logró obtener e interpretar parte de la visión de la Facultad de Ingeniería en cuanto a su responsabilidad social.
El hecho de construir la matriz de desempeño de las soluciones para PROSOFI utilizando la metodología AMC, implica un acercamiento inicial al proceso de toma de decisiones, ya que, para obtener dicha matriz, cada alternativa debe evaluarse con respecto a la totalidad de los criterios acordados, generando una base adecuada de comparación entre soluciones. Desde este punto de vista, esta matriz puede convertirse en una lista de chequeo, la cual podría utilizarse como guía para el grupo decisor, exigiendo que el desempeño de cada alternativa sea evaluado para la totalidad de criterios considerados.
Para escoger la comunidad PROSOFI se tenían como posibles alternativas diecinueve localidades de Bogotá y dos municipios de Cundinamarca. El uso de la herramienta propuesta, CRIDE, dio visibilidad y aclaró el panorama por medio de la clasificación y ordenamiento de las alternativas en cinco opciones (en orden de preferencia decreciente): Usme, Ciudad Bolívar, Bosa, Santa Fe y Rafael Uribe. En consecuencia, se le recomendó al grupo decisor (comité de apoyo permanente), que eligiera la localidad PROSOFI a partir de ese grupo reducido de opciones. Es de resaltar que este resultado hubiera sido bastante difícil de alcanzar sin la utilización de una herramienta para el soporte de toma de decisiones como la que se desarrolló, teniendo en cuenta que se buscaba una decisión consensuada en la que participaran una cantidad importante de actores, cada uno con una valoración particular para los criterios de selección posibles, lo que dificultaba el proceso. Efectivamente, sobre la base de este primer resultado, el grupo decisor consideró que la segunda fase del diseño de PROSOFI, la cual consiste en escoger la comunidad específica, debía partir de las dos localidades mejor clasificadas (Usme y Ciudad Bolívar). La herramienta CRIDE servirá de apoyo en esta nueva fase del diseño de PROSOFI.
CRIDE es una herramienta de soporte a la toma de decisiones que ayuda a seleccionar la alternativa más conveniente teniendo en cuenta múltiples intereses y criterios, pero no toma la decisión final ni sustituye a los decisores. En efecto, el AMC ayuda a que una toma de decisiones grupal sea racional, permita responder al por qué de la decisión y se pueda tener capacidad de auditoría debido a la trazabilidad en el proceso. En el caso del presente estudio, se observó que la visión de los criterios y pesos por parte de la Facultad de Ingeniería, direccionaron la toma de decisiones sin que necesariamente todos los participantes conocieran de manera profunda cada una de las alternativas, lo que facilitó el proceso de toma de decisión.
La utilización de métodos AMC innovadores ayuda a generar consenso, proporciona participación y apropiación a proyectos, y permite tener trazabilidad, estructura y rigor en la toma de decisiones. Adicionalmente, el AMC otorga visibilidad en la toma de decisiones cuando se tiene una gran cantidad de criterios y alternativas. Las características mencionadas anteriormente, no se encuentran de manera general en procesos de selección comúnmente utilizados como los procesos de votación, y por lo tanto se recomienda la utilización de herramientas AMC para la toma de decisiones corporativas.
Se espera seguir desarrollando la herramienta CRIDE con el fin de lograr una toma de decisiones que interprete de forma más adecuada y realista la visión de un grupo. En ese sentido, se modificará la herramienta de manera que contemple: (i) la variabilidad en los pesos asignados a cada criterio y en la calificación que recibe cada una de las alternativas usando el método de Monte Carlo; (ii) la variabilidad en los sentidos de preferencia de los criterios por medio de funciones de pertenencia típicas de la lógica difusa; y (iii) una mejor eficiencia en la construcción de la matriz de desempeños en cuanto al levantamiento y calificación de cada alternativa contemplando etiquetas lingüísticas.
Adicionalmente, se desarrollarán métodos de análisis de sensibilidad, robustez y redundancia de criterios, contemplando la incertidumbre y la precisión en la calificación de cada alternativa respecto a cada criterio y realizando pruebas estadísticas paramétricas y no paramétricas (pruebas de correlación, análisis de clústeres, análisis de componentes principales, entre otros) (Moura, 2008). Lo anterior otorgará guías que permitan construir matrices de desempeño y determinar características de los criterios (sentidos de preferencia, importancias) necesarios para llevar a cabo una toma de decisiones multicriterio utilizando la herramienta CRIDE desarrollada y evitar desgastes corporativos innecesarios.
NOTAS AL PIE DE PÁGINA
1. Proyecto financiado por CeiBA-Complejidad.
2. Originalmente cride es una palabra de origen celta que significa "corazón" (Davis, 2001, p. 106).
REFERENCIAS BIBLIOGRÁFICAS
1. Araújo, A., Rogério, P. y Dantas, M. (2007). Applying a decision making model in the early diagnosis of Alzheimer’s disease. En J.G. Carbonell y J. Siekmann (Eds.), Rough sets and knowledge technology. Lecture notes in computer science (pp. 149-156). Berlin: Springer-Verlag.
2. Baptista, M., Barraud, S., Alfakih, E., Nascimento, N., Fernandes, W., Moura, P. y Castro, L. (2004). Proposal of an evaluation system for urban storm drainage. Documento no publicado presentado en 5th International Conference on Sustainable Techniques and Strategies in Urban Water Management, Lyon, Francia.
3. Belacel, N. (2000). Multicriteria assignment method PROAFTN: Methodology and medical application. European Journal of Operational Research, 125(1), 175–183.
4. Ben-Arieh, D. y Chen, Z. (2006). Linguistic-labels aggregation and consensus measure for autocratic decision making using group recommendations. IEEE Transactions on Systems, Man, and Cybernetics—Part a: Systems and Humans, 36(3), 558–568.
5. Cámara de Comercio de Bogotá. (2009). Observatorio de Seguridad en Bogotá. Balance enero – junio de 2009. Observatorio, 37, 1-50.
6. Carlsson, C. y Fullér, R. (2000). Multiobjective linguistic optimization. Fuzzy sets and systems, 115(2000), 5-10.
7. Chen, C. y Hung, W. (2009). Applying ELECTRE and Maximizing Deviation Method for Stock Portfolio Selection under Fuzzy Environment. En Opportunities and Challenges for Next-Generation Applied Intelligence (pp. 85-92). Berlin: Springer-Verlag.
8. DANE. (2005). Censo General 2005. Nivel nacional. Bogotá: Autores.
9. Davis, D. (2001). The Development of Celtic Linguistics, 1850-1900 (Logos Studies in Language and Linguistics). Londres: Routledge.
10. Delgado, M., Herrera, F., Herrera-Viedma, E. y Martinez, L. (1998). Combining numerical and linguistic information in group decision making. Journal of Information Sciences, 107 (1998), 177–194.
11. Doumpos, M. y Zopounidis, C. (1998). A multicriteria decision aid methodology for sorting decision problems: The case of financial distress. Computational Economics, 14(3), 197–218.
12. Doumpos, M. y Zopounidis, C. (2004). Multicriteria decision aid classification methods. New York, NY: Kluwer Academic Publishers.
13. Figueira, J., Mousseau, V. y Roy, B. (2005). ELECTRE methods. En J. Figueira, G. Salvatore y M. Ehrgott (Eds.), Multiple criteria decision analysis: State of the art surveys (pp. 133-162). Boston, MA: Springer Science + Business Media.
14. Goh, C.H., Tung, Y.C.A. y Cheng, C.H. (1996). A revised weighted sum decision model for robot selection. Computers and Industrial Engineering, 30(2), 193–199.
15. Hajkowicz, S. y Collins, K. (2006). A review of multiple criteria analysis for water resource planning and management. Water Resources Management, 21(9), 1553–1566.
16. Hajkowicz, S. y Higgins, A. (2006). A comparison of multiple criteria analysis techniques for water resource management. European Journal of Operational Research, 184(1), 255–265.
17. Howard, A.F. (1991). A critical look at multiple criteria decision making techniques with reference to forestry applications. Canadian Journal of Forest Research, 21, 1649–1659.
18. Moura, P. (2008). Méthode d’évaluation des performances de systèmes d’infiltration des eaux de ruissellement en milieu urbain. Tesis doctoral no publicada, L’Institut National des Sciences Appliquées de Lyon, Lyon, France.
19. RAC - Resource Assessment Commission. (1992). Multi-Criteria Analysis as a Resource Assessment Tool. Canberra, Australia: Resource Assessment Commission of Australia.
20. Roy, B. (1967). A propos de l’agregation d’ordres complets: Quelques considérations théoriques et practiques. En La Décision – Agrégation et dynamique des ordres de préférence (pp. 225-239). Aix-en- Provence: CNRS.
21. Roy, B. (1968). Classement et choix en présence de points de vue multiples (la méthode ELECTRE). La Revue d’Informatique et de Recherche Opérationnelle (RIRO), 21(8), 57–75.
22. Roy, B. (1971). Problems and methods with multiple objective functions, Mathematical programming, 1(2), 239-266.
23. Roy, B. (1974). Critères multiples et modélisation des préférences -l’apport des relations de surclassement. Revue d’Économie Politique, 84(1), 1–44.
24. Roy, B. (2005). Paradigms and challenges. En J. Figueira, G. Salvatore y M. Ehrgott (Eds.), Multiple criteria decision analysis: State of the art surveys (pp. 3-26). Boston, MA: Springer Science + Business Media.
25. Roy, B. y Bertier, B. (1971). La méthode ELECTRE II: une méthode de classement en présence de critères multiples. En Nota de trabajo 142 (pp. 291-302). Paris: Grupo Metra.
26. Smith, Q.R., Mesa, S.O., Dyner, R.I., Jaramillo, A.P., Poveda, J.G. y Valencia, R.D. (2000). Decisiones con múltiples objetivos e incertidumbres. Medellín, Colombia: Facultad de Minas, Universidad Nacional de Colombia sede Medellín.
27. Subsecretaría de Planeación Socio-económica. (2007). Encuesta Calidad de Vida 2007 para Bogotá ECVB-2007. Recuperado el 11 de noviembre de 2009, de sitio DANE: http://www.dane.gov.co/files/investigaciones/condiciones_vida/ecvb/ECVB_07.pdf
28. Uzoka, F., Osuji, J. y Obot, O. (2011). Clinical decision support system (DSS) in the diagnosis of malaria: A case comparison of two soft computing methodologies. Expert Systems with Applications, 38(3), 1537–1553.
29. Weinhardt, C. y Seifert, S. (2010). Developments in GDN Research: Introduction. Group Decision and Negotiation, 19(2), 107-109.
30. Xu, Z. (2005). A Method Based on IA Operator for Multiple Attribute Group Decision Making with Uncertain Linguistic Information. FSKD, 1, 284-293.