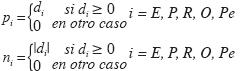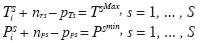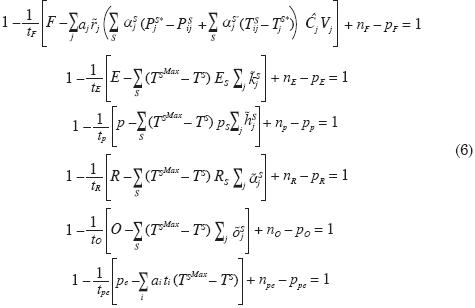LA MAXIMIZACIÓN DEL BENEFICIO
EN LAS EMPRESAS DEPURADORAS
DE AGUAS RESIDUALES.
EL CASO DE VALENCIA (ESPAÑA)1
JOSÉ MANUEL BROTONS MARTÍNEZ, Ph.D.*
Profesor titular Economía Financiera y Contabilidad, Universidad Miguel Hernández, España.
jm.brotons@umh.es
* Dirigir correspondencia a: Avda. de la Universidad s/n, Edificio La Galia, Universidad Miguel Hernández,
03202 Elche, Alicante, España.
Fecha de recepción: 05-03-2010 Fecha de corrección: 05-05-2010 Fecha de aceptación: 06-07-2011
RESUMEN
El estudio propone un sistema de maximización de beneficios de una estación
depuradora de aguas residuales (EDAR). La presencia de objetivos múltiples
impide su consecución simultánea, por lo que se considerará suficiente la
consecución de un determinado grado de satisfacción para cada uno de ellos.
En ocasiones, resulta muy complicado este último planteamiento, por lo que
se permitirán excepcionalmente ciertas violaciones de algunas restricciones,
lo que permite concluir que la programación por objetivos borrosa puede ser
un instrumento adecuado para este tipo de problemas. En consecuencia, las
EDAR tendrán una herramienta precisa para conseguir la maximización de
sus beneficios al que se añade un nuevo sistema de medición de la eficiencia
en el sector.
PALABRAS CLAVE
Financiación, aguas residuales, programación por objetivos borrosa.
Clasificación JEL: M00
ABSTRACT
Profit maximization at wastewater treatment plants. The case of
Valencia (Spain).
The main purpose of this paper is
to design a new way to maximize
the profit of wastewater treatment
plants (WWTP). The establishment
of multiple goals impedes their simultaneous achievement. As a result, it
will be enough to achieve a certain
degree of satisfaction of each goal.
Sometimes this approach can be extremely difficult, so minor violations
of some restrictions are exceptionally
allowed. Fuzzy goal-based scheduling
can be considered a suitable tool for
these kinds of problems. In short,
WWTPs will have a suitable tool for
achieving profit maximization, and,
at the same time, there will be a
new system to measure efficiency in
the sector.
KEYWORDS
Financing, wastewater, fuzzy goalbased program.
RESUMO
A maximização do lucro nas
empresas depuradoras de águas
residuais. O caso de Valência
(Espanha)
O estudo propõe um sistema de maximização do lucro de uma estação
de tratamento de águas residuais
(ETAR). A presença de múltiplos
objetivos impede a sua realização em
simultâneo, pelo que será considerado suficiente atingir um determinado
grau de satisfação para cada um
deles. Por vezes essa última abordagem é muito complicada, pelo que se
permitirão excepcionalmente certas
violações de algumas restrições, o
que permite concluir que a programação por metas difusa pode ser um
instrumento adequado para esse tipo
de problemas. Portanto, as ETAR terão uma ferramenta adequada para
atingir a maximização de seus lucros
ao qual é adicionado um novo sistema
de medição da eficiência no setor.
PALAVRAS-CHAVE
Financiamento, águas residuais, programação por metas difusa.
INTRODUCCIÓN
La programación multiobjetivo es
una herramienta adecuada para la
modelización de problemas de toma
de decisión en el mundo real, especialmente cuando existe conflicto
entre los múltiples objetivos (Lee y
Wen, 1997). En estos casos resulta
necesario una ordenación de los
mismos y si es posible, su ponderación. Además, una de sus mayores
limitaciones viene del hecho de que
el nivel de aspiración o la prioridad
de los objetivos, y ocasionalmente
los pesos asignados a éstos, son imprecisos para el decidor financiero.
En esas circunstancias, la teoría de
los subconjuntos borrosos permite
una adecuada cuantificación de los
mismos y su correcta implementación en un problema de toma de
decisiones.
El problema hídrico ha sido abordado
recientemente en trabajos como los de
Méndez y Méndez (2010); así como
numerosos trabajos han abordado el
tema de la programación multiobjetivo en los recursos hídricos (Dauer
y Krueger 1980; Haimes, Tarvainen,
Shima y Thadathil, 1990; Loucks,
1977). Por su parte, las aplicaciones
de la programación multiobjetivo en
la administración de la calidad del
agua no son demasiado frecuentes,
destacan los trabajos de Steuer y
Wood (1986) que consideran el método de Tchebycheff de la programación
0-1 para conseguir agua de calidad
y Lai, Lin y Hwang (1994) quienes
desarrollaron una técnica para ordenar preferencias por similitud con
un método de solución ideal para
desarrollar en el valle del río Bow. A
este respecto, Lee y Wen (1995) abordaron la aplicación de programación
multiobjetivo para la administración
de agua de calidad en una cuenca
hidrográfica y luego, en otro trabajo,
introdujeron la metodología fuzzy
para este mismo propósito (Lee y
Wen, 1996). Otras aplicaciones de
la metodología fuzzy en el ámbito
empresarial pueden consultarse en
Medina y Manco (2007) y Herrera y
Osorio (2006).
La situación hídrica en España es
preocupante (Terceño, Brotons y
Trigueros, 2009), por lo que adquiere
una gran importancia la depuración
de aguas residuales.
Las comunidades autónomas son las
encargadas de sufragar los gastos de
la depuración de aguas residuales
en España. A este respecto, es la Comunidad Valenciana la que presenta
una normativa más extensa sobre el
particular. Los modelos de financiación, regulados por la Orden de 14
de abril de 1993 (Consellería d’Obres
Públiques, Urbanisme i Transports)
sirven de base para tal propósito. Según estos, para determinar los gastos
financiables:
Se agregan los costes de energía
eléctrica, personal, reactivos y otros
costes, se procede a su separación en
fijos y variables, para los primeros
se calcula el coste diario, y para los
segundos el coste por metro cúbico
depurado, y la financiación para cada
periodo se obtendrá multiplicando el
coste medio diario por el número de
días del periodo a financiar, más el
coste por metro cúbico por el volumen
depurado. (Terceño, Brotons y Trigueros, 2007b, p. 124)
Al resultado se le agrega un porcentaje en concepto de gastos generales.
De acuerdo con Terceño, Brotons y
Trigueros (2007a), el sistema actual
adolece de importantes deficiencias,
entre las que destacan la imposibilidad de financiar todos los gastos y el
cálculo del beneficio industrial como
un porcentaje de los costes totales,
con base en las cuales se ha propuesto
su sustitución por otro, no basado en
la financiación de los costes reales,
sino en los costes estándares o medias
de la comunidad.
El reparto de los costes comunes,
tal y como se expone a lo largo del
apartado dedicado a la financiación
de la estación depuradora de aguas
residuales (EDAR), debe realizarse
en base al Valor Neto de Realización
(VNR). Sin embargo, esto exige el
conocimiento del precio de mercado
de todos los productos obtenidos en el
proceso de depuración, pero el precio
del agua depurada es incierto por no
existir en la actualidad mercado para
el mismo. Es por ello que la matemática fuzzy o borrosa se convierte
en un instrumento adecuado para el
tratamiento de esta incertidumbre.
Con base en este planteamiento se
propone, en primer lugar, determinar un sistema de medición de la
eficiencia en una EDAR que tenga
en cuenta tanto la reducción de los
costes de cada uno de los procesos,
como la consecución de los objetivos
de calidad, ya sea en el porcentaje de
reducción de la carga contaminante
como en los niveles del efluente. A
partir de este sistema de medición
de la eficiencia y del modelo de financiación de las EDAR, se plantea
la exigencia de maximización de su
beneficio.
En consecuencia, este trabajo se
estructura en los siguientes cinco
apartados: en el primero se presentan las notaciones sobre matemática
fuzzy utilizadas, en el segundo una
breve introducción a la programación por objetivos fuzzy. En el
tercero se propone el nuevo modelo
de financiación basado en los costes
reales de la depuración del agua residual y considerando que los costes
asociados a fangos deshidratados y
electricidad pueden recuperarse a
través de su venta. En el cuarto se
introduce la eficiencia en el modelo,
y por último, en el quinto se presenta la programación por objetivos
que deberá seguir la empresa para
maximizar sus beneficios.
1. CONCEPTOS PREVIOS
Y NOTACIÓN
Un subconjunto borroso à es un subconjunto definido sobre el conjunto
de referencia X para el que el nivel de
pertenencia de un elemento x  X a Ã
acepta valores diferentes a 0 y 1. Un
subconjunto borroso à puede ser definido como à = {x, μà (x)/x
X a Ã
acepta valores diferentes a 0 y 1. Un
subconjunto borroso à puede ser definido como à = {x, μà (x)/x  X} donde μà (x)
se denomina función de pertenencia
y es una aplicación μà (x)
X} donde μà (x)
se denomina función de pertenencia
y es una aplicación μà (x) [0,1] . Un α
-corte es un conjunto ordinario (crisp)
que contiene elementos cuyo nivel de
pertenencia es al menos α. Para un
subconjunto borroso Ã, se denotará
un α -corte con Ãα siendo su expresión
matemática:
[0,1] . Un α
-corte es un conjunto ordinario (crisp)
que contiene elementos cuyo nivel de
pertenencia es al menos α. Para un
subconjunto borroso Ã, se denotará
un α -corte con Ãα siendo su expresión
matemática:
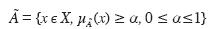
Se denotará por à = (αL, αC, αR) a
los números borrosos triangulares
(NBT), donde αL, αC y αR representan, respectivamente, el extremo
izquierdo, el centro y el extremo
derecho. Otra forma de representar
estos números es mediante sus radios
izquierdo (lA) y derecho (rA): Ã = (αL, lA,
rA). Estos son los números borrosos
más extendidos ya que son fáciles de
usar y pueden ser interpretados de
forma fácil.
2. LA PROGRAMACIÓN
POR OBJETIVOS FUZZY
Charnes y Cooper (1961) introdujeron
la programación por objetivos. Una
de sus principales ventajas es que
permite alcanzar directamente, para
problemas multiobjetivo, una solución de compromiso. Sin embargo, su
principal problema es que el decisor
debe especificar exactamente los objetivos, sin considerar que éstos son
imprecisos. Con la matemática fuzzy,
propuesta inicialmente por Zadeh
(1965), se consiguió superar dicha
dificultad ya que permitió asignar
los objetivos de una forma imprecisa.
Si se utiliza la programación por objetivos fuzzy (Zimmermann, 1978),
se puede asumir que el decisor
puede establecer en dicho programa
un nivel de aspiración gi para cada
objetivo, y que algunas restricciones
pueden violarse ligeramente. A partir
de ahora, ya no se distinguirá entre
objetivos y restricciones, ya que la
solución del problema debe cumplir
ambos con un determinado grado de
satisfacción. En este caso, el modelo
podría escribirse así:
Encontrar:
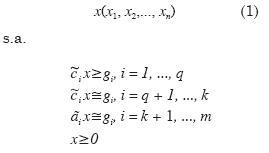
Donde los símbolos 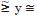 indican que
las ecuaciones o inecuaciones son flexibles y que tienen una interpretación
del tipo "esencialmente mayor que" o
"aproximadamente igual que", respectivamente. De acuerdo con Rommel-fanger y Slowinski (1998) se puede
interpretar la restricción
indican que
las ecuaciones o inecuaciones son flexibles y que tienen una interpretación
del tipo "esencialmente mayor que" o
"aproximadamente igual que", respectivamente. De acuerdo con Rommel-fanger y Slowinski (1998) se puede
interpretar la restricción 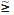 como:
como:
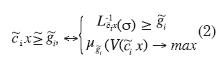
Donde σ  [0,1] es un parámetro que
puede ser usado por el decisor dependiendo de su grado de aversión al
riesgo. De forma similar se pueden interpretar las restricciones de tipo
[0,1] es un parámetro que
puede ser usado por el decisor dependiendo de su grado de aversión al
riesgo. De forma similar se pueden interpretar las restricciones de tipo 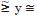 . Los objetivos están caracterizados
por sus correspondientes funciones de
pertenencia. Si el margen de tolerancia se representa por ti, para restricciones del tipo
. Los objetivos están caracterizados
por sus correspondientes funciones de
pertenencia. Si el margen de tolerancia se representa por ti, para restricciones del tipo 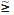 , y el valor central
del número borroso
, y el valor central
del número borroso 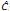 ix se denota por
cix . La función de pertenencia puede
expresarse:
ix se denota por
cix . La función de pertenencia puede
expresarse:
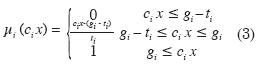
La interpretación de las restricciones
del tipo  es similar.
es similar.
3. FINANCIACIÓN
DE LAS EMPRESAS EDAR
En la mayoría de países la depuración
es financiada por las distintas administraciones, pero existen otros en
los que se financia a través del cobro
de un canon a los consumidores de
aguas potables. Se trata de sistemas
muy similares, ya que en el primer
método la administración determina la cantidad a financiar, y en el
segundo, una vez establecida dicha
cantidad, se repercute sobre el consumo estimado de agua potable. Ambos
presentan importantes deficiencias:
se financian costes de productos que
luego se venden en el mercado (fangos
y electricidad), y se consideran unos
parámetros mínimos de calidad, pero
no se incentiva su mejora (Terceño et
al., 2007b).
Aunque el número de fases que se
aplican a la depuración dependen
de la calidad del agua que se desea obtener, en términos generales
suelen agruparse en cuatro: pretratamiento, tratamiento primario,
secundario y terciario. En la Tabla
1 se enumeran los procesos de depuración, con especificación del tipo de
tratamiento al que corresponden, el
tipo de EDAR y la línea de tratamiento. Las combinaciones que se pueden
dar son bastante variadas. A modo de
ejemplo, se muestra en el Gráfico 1 la
EDAR de Algorós (Elche).
TABLA 1
 Una vez identificados los procesos, se
Una vez identificados los procesos, se
les afectarán todos los costes a los productos, tanto directos como indirectos,
con el objeto de que sean comparables
entre EDAR diferentes, salvo aquellos
que no guardan ninguna relación con
las primeras, que serán imputados
a los productos que se denominarán
costes específicos CAE. De esta forma,
se podrá conseguir una comparación
mucho más homogénea entre EDAR,
a través de los costes por metro cúbico depurado (Cj) de cada una de
sus procesos. El último paso será
la imputación a los productos de los
costes anteriormente calculados, de
acuerdo con determinados criterios
de reparto.
Los costes de cada sección j por metro
cúbico depurado pueden agruparse
en las siguientes categorías: energía
eléctrica (Ej), personal (Pj), reactivos
(Rj) y otros costes (Oj). A su vez, la
energía eléctrica se descompone en
kilowatios-hora contratados (Kt) y
kilowatios-hora consumidos (CS),
siendo sus precios Pt y PS , respectivamente. El coste de personal se deberá
separar en horas consideradas como
fijas (hFi) y variables (hVi), con sus respectivos precios PF y PV . El coste del
reactivo s por metro cúbico depurado
(Vj) en la sección j será αSj . Por último,
los otros costes se agrupan en fijos
(Ofj) y variables (OVj). En resumen,
los costes unitarios para la sección j
son: Cj = PtKtj + PS KSj + PFhFj +PVhVj +Vj∑j
αSjPj +OFj +OVj .
El último paso será la imputación a
los productos de los costes anteriormente calculados, de acuerdo con
un criterio de reparto adecuado. La
financiación deberá cubrir únicamente aquella parte de los costes que correspondan al agua depurada, único
producto que no puede venderse por
impedirlo el Real Decreto Legislativo
1/2001 (Ministerio de Medio Ambiente, 2001), por el que se aprueba el
Texto Refundido de la Ley de Aguas,
ya que el resto podrá recuperarse con
la venta de los fangos deshidratados
y la electricidad.
Se plantea como objetivo el establecimiento de un sistema de financiación
para el sector que permita cubrir sus
costes, pero que premie a aquellas
empresas que consigan una reducción
de los mismos y una mejora de los
parámetros de depuración. Para ello
habrá que determinar los costes medios de cada proceso (en el ámbito de
aplicación de este modelo), mediante
una correcta asignación de los costes
indirectos. A este respecto, Horngren,
Foster y Datar (1996) indican que en
el caso de empresas sujetas a regulación o en las que no haya mercado
de referencia para fijar los precios,
éstos deben establecerse a partir de
los costes incurridos. La Norma Internacional de Contabilidad Nº2 (NIC 2,
2005) establece que cuando los costes
de transformación de cada tipo de
producto no sean identificables por
separado, se distribuirá el coste total
entre los productos, utilizando bases
uniformes y racionales. Hemmer
(1996), Wang (1996) y Deakin y Maher (1991) proponen el reparto de los
costes comunes entre los productos de
acuerdo con su VNR.
Este criterio de separación de los
costes comunes presenta la dificultad
del cálculo del precio de mercado del
agua depurada.
Al no haber un mercado de agua
depurada, no existen datos sobre
sus precios que permitan estimar su
VNR. Dado que el precio es incierto,
habrá que estimarlo a partir del precio que estarían dispuestos a abonar
los demandantes, o el que solicitan los
oferentes. Por ello, la variable precio
del agua puede ser considerada como
un número borroso triangular (NBT):
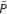 A(Pa, Pb, Pc), donde Pa es el mínimo, Pc
el máximo, y Pb el valor más posible,
siendo sus α -cortes
A(Pa, Pb, Pc), donde Pa es el mínimo, Pc
el máximo, y Pb el valor más posible,
siendo sus α -cortes 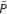 Aα = {x
Aα = {x  U / μ
U / μ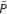 (x)
≥ α} = {α(Pb–Pa) + Pa, α (Pb – Pc) + Pc}.
(x)
≥ α} = {α(Pb–Pa) + Pa, α (Pb – Pc) + Pc}.
Los coeficientes de reparto del producto i ( i) serán el cociente en el punto de separación entre el valor del producto i y el del total de la producción.
A modo de ejemplo, el coeficiente de
reparto de costes asignados al agua
depurada es
i) serán el cociente en el punto de separación entre el valor del producto i y el del total de la producción.
A modo de ejemplo, el coeficiente de
reparto de costes asignados al agua
depurada es  A = A
A = A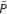 A/(A
A/(A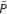 A + FPF + EPE),
siendo A, F y E las unidades producidas de agua, fangos y electricidad, y
A + FPF + EPE),
siendo A, F y E las unidades producidas de agua, fangos y electricidad, y
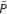 A, PF y PE, sus precios respectivos. Su
función de pertenencia será:
A, PF y PE, sus precios respectivos. Su
función de pertenencia será:

La propuesta de financiación se basa
en el conocimiento de los costes medios por metro cúbico depurado de
cada una de las secciones, y de su
eficiencia, de la que se hablará más
adelante.
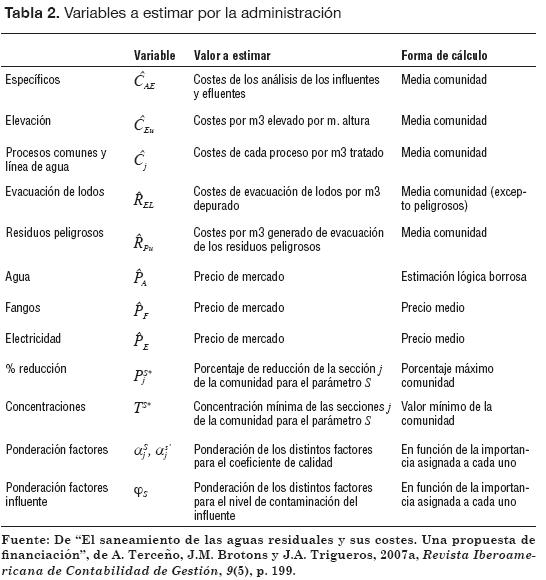
Valores de referencia
Para el conocimiento de los mismos,
la administración correspondiente
deberá estimar los precios de los
distintos productos (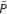 A,
A, 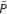 F y
F y 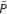 E) y los
costes medios por metro cúbico depurado de cada una de las secciones
(Cj). La administración encargada
de la financiación de la actividad de
depuración deberá obtener una serie
de variables representativas de la
depuración en el ámbito territorial
de su influencia. La financiación se
obtendrá por comparación entre dichos valores y los facilitados por cada
una de las EDAR, con los factores de
corrección suficientes. En concreto,
dichas variables son las que se citan
en la Tabla 2.
E) y los
costes medios por metro cúbico depurado de cada una de las secciones
(Cj). La administración encargada
de la financiación de la actividad de
depuración deberá obtener una serie
de variables representativas de la
depuración en el ámbito territorial
de su influencia. La financiación se
obtendrá por comparación entre dichos valores y los facilitados por cada
una de las EDAR, con los factores de
corrección suficientes. En concreto,
dichas variables son las que se citan
en la Tabla 2.
4. MEDICIÓN
DE LA EFICIENCIA
Para medir la eficiencia de una
EDAR, además de los aspectos económicos habrá que tener en cuenta
la reducción de la contaminación
conseguida, que habrá de medirse en
función de varios indicadores como
DBO5, DQO, SS, niveles de fósforo,
nitrógeno, etcétera. Además, para
cada uno de los anteriores, se valorará tanto el nivel final conseguido
como su porcentaje de reducción.
En primer lugar se seleccionarán los
indicadores relativos al porcentaje
de reducción de la carga contaminante y a los niveles del efluente,
a partir de los cuales se podrá calcular el nivel de eficiencia de cada
sección, exclusivamente en función
de los niveles de calidad conseguidos
o incluyendo también los aspectos
económicos si se pondera el nivel de
costes conseguido.
Para la formulación del modelo de
medición de la eficiencia de una
EDAR, se definen las variables "porcentaje de reducción del parámetro
s para la sección j de la EDAR i Psij",
"porcentaje de reducción máximo del
parámetro s en la sección j en todas
las EDAR de una comunidad autónoma (Ps*j)", "concentración del parámetro s en el efluente de la sección j de
la EDAR i (TSij)", y "mínimo valor de
concentración en los efluentes de la
sección j de la comunidad autónoma
para el parámetro s TS*j".
Para cada uno de los parámetros
que miden la mejora de la calidad
del agua depurada, habrá que obtener tanto la reducción como su
concentración en el efluente. Para la
valoración del primero, se define δS*ij
como la distancia entre el porcentaje
de reducción del parámetro S en la
sección j de la depuradora i, y el valor objetivo (mínimo valor de dicho
parámetro en la sección j de todas
las depuradoras de la comunidad
autónoma) δS*ij = PS*j - PS*ij. De la misma
manera se puede definir la distancia
entre el nivel de contaminación del
efluente de la sección j, conseguido
en la EDAR i y el mínimo de toda la
comunidad (ΔS*ij), ΔSij = TSij - TS*j.
El objetivo técnico será conseguir,
para los parámetros seleccionados
por la administración, que los valores
δSij y ΔSij sean mínimos para todo s.
Sin embargo, todas estas variables no
evolucionan de la misma forma, por
lo que habrá que ponderar para cada
sección su importancia relativa. La
distancia del porcentaje de reducción
de la sección j respecto al valor objetivo para el parámetro s, se ponderará
con un coeficiente αSj. Por su parte, la
distancia del nivel de concentración
del efluente de la sección j respecto al
valor objetivo para el parámetro S, se
ponderará con un coeficiente αS'j, de
manera que ∑jαSj = ∑jαS'j=1, siendo ∑jαS
la importancia asignada a la reducción del porcentaje de contaminación
y∑jαS'j la asignada a la contaminación
del efluente resultante.
La agregación de todas las distancias
con respecto a los valores de contaminación y porcentajes de reducción objetivos permitirá obtener la siguiente
función de ineficiencia del proceso j de
la EDAR  , y la
función de eficiencia de dicho proceso j será,
, y la
función de eficiencia de dicho proceso j será, 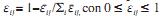 1,
para el conjunto de la EDAR, si
a cada sección se le asigna una
importancia ωj tal que ∑jωj = 1,
la función de ineficiencia será
1,
para el conjunto de la EDAR, si
a cada sección se le asigna una
importancia ωj tal que ∑jωj = 1,
la función de ineficiencia será
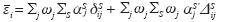
y la de eficiencia,
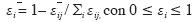
Una vez expuesta la forma de obtener
la financiación, habrá que multiplicar
los costes estimados por el volumen
depurado y por un factor (1+ εij). Además, dado que la importancia de la
eficiencia técnica no es la misma en
todas las secciones, habrá algunas en
las que una reducción de la contaminación sea mucho más costosa que en
otras. En consecuencia, habrá que utilizar un nuevo factor de ponderación
que incorpore tanto la dificultad de la
reducción de la contaminación en una
sección, como el premio que se ofrezca
por la mejora de la eficiencia técnica.
En cualquier caso, debe ser la entidad
encargada de abonar la financiación
la que decida la importancia que se
asigna a la mejora cualitativa de los
caudales depurados. Dicho factor,
que se denota por αj, dependerá de
la valoración que la administración
haga de la dificultad de un proceso
en mejorar su calidad. La financiación de la sección j de la EDAR i (Fij),
si su coste medio estimado es 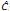 j, su
eficiencia calculada εi, y su volumen
depurado Vij, será
j, su
eficiencia calculada εi, y su volumen
depurado Vij, será 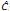 .
En consecuencia, la financiación total
podría resumirse en la Tabla 3.
.
En consecuencia, la financiación total
podría resumirse en la Tabla 3.

5. MAXIMIZACIÓN DEL
BENEFICIO DE LAS EDAR
La presencia de objetivos múltiples
hace imposible que se puedan conseguir todos a la vez, por lo que es
preferible plantearse la consecución
de un determinado grado de satisfacción para cada uno de ellos. Además,
pueden aceptarse ciertas violaciones
de algunas restricciones, por lo que
se considera que la programación
por objetivos borrosa puede ser un
instrumento adecuado para este tipo
de problemas.
Por ello se plantean los siguientes
cuatro grupos de objetivos para conseguir la maximización de los beneficios
en una EDAR: i) restricciones técnicas, ii) maximización de los ingresos
por financiación de cada sección j,
iii) minimización de los costes, y iv)
minimización de las penalidades por
bajo rendimiento.
6. RESTRICCIONES
El Real Decreto-Ley 11/1995 (Gobierno, 1995), por el que se establecen las
normas aplicables al tratamiento de
las aguas residuales urbanas, exige
que los efluentes presenten unos
niveles de concentración máximos
y que éstos se hallan reducido con
respecto a los influentes en un determinado porcentaje para cada uno
de los parámetros especificados en la
normativa. Estos niveles son inviolables y deberán de conseguirse por
las EDAR para lograr la financiación
propuesta. De esta forma, si existen S
parámetros, el nivel de concentración
del efluente de la EDAR i para el
parámetro s , nivel de concentración
del último proceso de la EDAR en el
que se trata el licor (TSi) , deberá ser
inferior al valor máximo (TSMax), es decir, 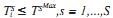 . Por su parte,
el porcentaje de reducción total de la
depuradora i para el parámetro s (PSi)
deberá ser superior al valor mínimo
(PSmin) y no se aceptan violaciones de
las mismas,
. Por su parte,
el porcentaje de reducción total de la
depuradora i para el parámetro s (PSi)
deberá ser superior al valor mínimo
(PSmin) y no se aceptan violaciones de
las mismas, 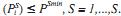
6.1. Maximización de los ingresos
por financiación de la sección j 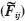
La financiación de una sección depende del coeficiente de reparto ( A), de la
importancia que se asigna a la mejora
cualitativa de los caudales depurados
en la misma (aj), de la eficiencia conseguida (εij), de los costes estimados
(
A), de la
importancia que se asigna a la mejora
cualitativa de los caudales depurados
en la misma (aj), de la eficiencia conseguida (εij), de los costes estimados
(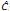 j) y del caudal depurado (Vj).
j) y del caudal depurado (Vj).
La importancia asignada a cada sección y los costes estimados, son fijados
por la administración encargada de la
financiación. El caudal depurado es un
dato exógeno, el coeficiente de reparto
depende del citado caudal y del diseño
de la planta, por lo que la EDAR no
puede influir sobre ninguno de los dos.
En consecuencia, el objetivo será:
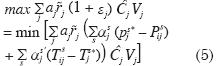
Esto es, 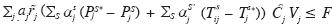 . En este tipo de
objetivos (restricciones), resulta muy
complejo definir un valor máximo que
no se pueda sobrepasar por lo que
resulta muy aconsejable considerar
una restricción con un cierto grado
de imprecisión (borrosa).
. En este tipo de
objetivos (restricciones), resulta muy
complejo definir un valor máximo que
no se pueda sobrepasar por lo que
resulta muy aconsejable considerar
una restricción con un cierto grado
de imprecisión (borrosa).
6.2. Minimización de los costes
Los costes de las EDAR se agrupan en
cuatro grandes categorías: energía,
personal, reactivos y otros costes. El
objetivo de la empresa será conseguir
los niveles de contaminación mínimos
que le permitan mejorar la financiación. La empresa debe fijar para cada
uno de estos gastos un objetivo deter-minado, pero se permitirán ciertas
violaciones de este objetivo:
6.3. Minimización de las penalidades por bajo rendimiento
La empresa deberá minimizar las
penalidades que se le imponen si
la calidad del efluente no alcanza
los mínimos requeridos durante
un determinado periodo. Se suele
sancionar con una cantidad fija por
unidad que sobrepase la concentración máxima y por día (ai) en que el
rendimiento no fuese el adecuado,
siendo ti el número de días en que
se sobrepasa dicho máximo. Aunque no es deseable, de igual forma
se permiten ciertas violaciones de
esta restricción 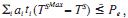 siendo ti el número de días en que no
se alcanzan los mínimos requeridos.
En el entorno de la decisión fuzzy, el
objetivo es maximizar cada una de
las funciones de pertenencia asociadas a cada uno de los objetivos. Se
denotará por tF, tE, tP, tR, tO y tPe, los límites de tolerancia correspondientes
a los niveles de aspiración F, E, P, R,
O y Pe; por KSj, HSj, ASj, OSj , los valores
centrales de los números borrosos
siendo ti el número de días en que no
se alcanzan los mínimos requeridos.
En el entorno de la decisión fuzzy, el
objetivo es maximizar cada una de
las funciones de pertenencia asociadas a cada uno de los objetivos. Se
denotará por tF, tE, tP, tR, tO y tPe, los límites de tolerancia correspondientes
a los niveles de aspiración F, E, P, R,
O y Pe; por KSj, HSj, ASj, OSj , los valores
centrales de los números borrosos
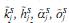 y por Z la función objetivo
donde PTI,..., PTS PPI,..., PPS , PF, PC y PPe
representan los niveles de prioridad,
que presentan la siguiente relación:
PTI »... »... PTS » PPI »...» PPS » PF » PC »
PPe » i = 1 ... S.
y por Z la función objetivo
donde PTI,..., PTS PPI,..., PPS , PF, PC y PPe
representan los niveles de prioridad,
que presentan la siguiente relación:
PTI »... »... PTS » PPI »...» PPS » PF » PC »
PPe » i = 1 ... S.
Por su parte, si se denota por di la
diferencia entre el valor meta y el
nivel alcanzado, y sustituyendo dichas variables por dos variables no
negativas, esto es ni y pi (desviaciones
negativas y positivas), donde:
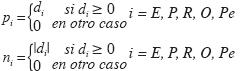
De esta forma, el programa podría
escribirse como:
Hallar , T1, ..., TS, P1, ... , PS, que minimice, Z = PT1 pT1 + ... + PTS pTS + PP1 nP1+
... + PPS nPS + PF pF + PC(pE + pp + pR + p) +
PPE PPE; tal que,
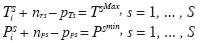
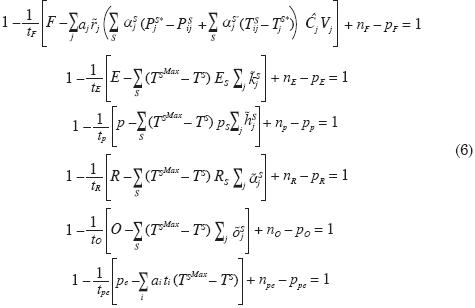
Siendo,

Si es posible asignar un peso a cada
una de las metas, la función objetivo
quedará como:

Con ∑ 2S+3i=1 ωi = 1; y el programa podría
resolverse por programación lineal.
7. CONCLUSIONES
En el contexto de un nuevo modelo
de financiación para el sector de las
empresas depuradoras de aguas residuales, ya propuesto en otros trabajos
como Terceño et al. (2007a, 2007b), en
el presente artículo se han planteado
como objetivos principales la determinación de un sistema de medición de
la eficiencia para el sector y la determinación de los parámetros técnicos
y económicos que maximicen los beneficios de la empresa. Las empresas
deben asignar a cada proceso todos
los costes que le sean imputables, a
fin de que dicho proceso sea comparable con el del resto de depuradoras
de la Comunidad Autónoma objeto de
estudio. Si todas las EDAR realizan
estos cálculos de forma similar, la
administración podrá estimar un coste medio por metro cúbico depurado
para cada uno de los procesos.
El sistema propuesto se considera
que es eficiente ya que la financiación
se obtiene mediante la agregación de
los productos del coste unitario por el
volumen depurado en cada sección,
ponderados por un factor 1 + εi que
premia a las empresas que presenten
de una parte mayores reducciones de
carga contaminante, y de otra niveles
más bajos de la misma en el efluente.
Además, cada uno de los procesos
se pondera por un segundo factor a
fin de valorar su importancia en el
conjunto de la EDAR.
En cuanto al segundo de los objetivos,
para la maximización del beneficio
de las empresas se considera que la
programación por metas fuzzy, es
una herramienta adecuada para ser
utilizada ya que permite la introducción de diferentes objetivos o metas.
Además, cuando estos son imprecisos, como es el caso, el decisor no se
ve obligado a priorizar entre unos u
otros, sino que es suficiente con que
fije un nivel de aspiración para cada
uno. De la misma forma, también se
permiten ligeras violaciones de las
restricciones. El programa propuesto
plantea la necesidad de maximizar
los ingresos, minimizando los costes
de energía, personal, reactivos y otros
costes, y las penalidades por bajo
rendimiento.
Cuando los recursos hídricos se convierten en un bien escaso, la gestión
de los mismos es fundamental en sus
dos vertientes, la económica, ya que
la capacidad de producción de muchos
bienes depende de la existencia de
agua en condiciones suficientes y a
precios asequibles, y la medioambiental, por los perjuicios que acarrearía
al medio ambiente la existencia de
vertidos de agua no depurada. En
consecuencia, las futuras líneas de
investigación deberán abordar un
uso sostenible de los recursos hídricos que permita paliar los problemas
de escasez existentes en la actualidad, pero minimizando el impacto
medioambiental.
A pesar de los relevantes resultados
del modelo, es necesario reconocer sus
dificultades de aplicación, ya que ello
depende de la voluntad política del
legislador de la comunidad autónoma. Sin embargo, en un momento de
crisis como el actual, la mejora de la
eficiencia del sector incentivando el
ahorro de costes y la mejora del medio
ambiente debe ser prioritaria, por lo
que resulta especialmente apropiada
su implantación. Además, esto permitiría constatar los puntos fuertes
y débiles del modelo e introducir
las mejoras pertinentes. Un estudio
comparativo sobre la idoneidad del
presente modelo a otras áreas geográficas permitirá mejorar la presente
investigación en el futuro.
NOTAS AL PIE DE PÁGINA
1. El autor quiere agradecer a los revisores sus comentarios y sugerencias que han permitido mejorar el
trabajo inicialmente presentado.
REFERENCIAS BIBLIOGRÁFICAS
1. Charnes, A. y Cooper, W.W. (1961).
Management models and industrial applications of linear programming. New York, NY: Wiley.
2. Dauer, J.P. y Krueger, R.J. (1980).
A multiobjective optimization
model for water resources planning. Applied Mathematical Modelling, 4(3), 171-175.
3. Deakin, E.B. y Maher, M.W.
(1991). Cost accounting. Home-Homewood, IL: Irwin.
4. EPSAR. (s/f). Elx (Algoros). Recuperado de http://www.epsar.gva.es/sanejament/instalaciones/edar.aspx?id=105
5. Haimes, Y.Y., Tarvainen, K.,
Shima, T. y Thadathil, J. (1990).
Hierarchical Multiobjective Analysis of Large-Scale Systems. New
York, NY: Hemisphere Publishing
Corporation.
6. Hemmer, T. (1996). Allocations of
sunk capacity costs and joint costs
in a linear principal-agent model.
Accounting Review, 71(3), 419-432.
7. Herrera, M.F. y Osorio, J.C.
(2006). Modelo para la gestión de
proveedores utilizando AHP difuso.
Estudios Gerenciales, 22(99), 69-88. Recuperado de http://www.icesi.edu.co/biblioteca_digital/bitstream/item/810/2/Modelo_gestion_proveedores_utilizando_AHP_difuso.PDF
8. Horngren, C.T., Foster, G. y Datar,
S.M. (1996). Contabilidad de Costos. Un Enfoque Gerencial. México:
Prentice Hall Hispanoamericana.
9. Lai, Y.J., Lin, T.Y. y Hwang,
C.L. (1994). TOPSIS for MODM.
European Journal of Operational
Research, 76(3), 486-500.
10. Lee, C.S. y Wen, C.G. (1995). An
economic and environmental balance in a river basin using interactive multiobjective optimization.
Journal of Environmental Science
and Health (Part A), 30(8), 1727-1748.
11. Lee, C.S. y Wen, C.G. (1996).
Application of multiobjective programming to water quality management in a River Basin. Journal
of Environmental Management,
47(1), 11-26.
12. Lee, C.S. y Wen, C.G. (1997). Fuzzy
goal programming approach for
water quality management in a
river basin. Fuzzy Sets and System, 89(2), 181-192.
13. Loucks, D.P. (1977). An application
of interactive multiobjective water
resources planning. Interfaces,
8(1), 70-75.
14. Medina, S. y Manco, O. (2007).
Diseño de un sistema experto difuso:
evaluación de riesgo crediticio en
firmas comisionistas de bolsa
para el otorgamiento de recursos
financieros. Estudios Gerenciales,
23(104), 101-129. Recuperado de
http://bibliotecadigital.icesi.edu.co/biblioteca_digital/bitstream/item/1274/1/Diseno_sistema_experto_difuso.pdf
15. Méndez, J.A. y Méndez, J.M.
(2010). Tasas por utilización del
agua ¿instrumento de asignación
eficiente del agua o mecanismo
de financiación de la gestión
ambiental? Estudios Gerenciales,
26(115), 93-115. Recuperado de
http://bibliotecadigital.icesi.edu.co/biblioteca_digital/bitstream/item/4382/1/5Tasas_utilizacion.pdf
16. Norma Internacional de Contabilidad No. 2 -NIC2. (2005). Software.
Recuperado de http://www.normasinternacionalesdecontabilidad.es/nic/pdf/NIC02.pdf
17. Real Decreto Legislativo 1/2001,
por el que se aprueba el Texto
Refundido de la Ley de Aguas,
Ministerio de Medio Ambiente.
(2001). Recuperado de http://noticias.juridicas.com/base_datos/Admin/rdleg1-2001.html
18. Real Decreto Legislativo 11/1995,
por el que se establecen las Normas Aplicables al Tratamiento de
las Aguas Residuales Urbanas,
Gobierno. (1995).
19. Rommelfanger, H. y Slowinski, R. (1998). R. Fuzzy linear
programming with single or
multiple objective functions. En
R. Solowinski (Eds.), Fuzzy Sets in
Decision analysis. Operational Research and Statistics (pp. 179-214).
Boston, MA: Kuwler Academic
Publishers.
20. Steuer, R.E. y Wood, E.F. (1986).
On the 0-1 implementation of the
Tchebycheff solution approach: a
water quality illustration. Large
Scale Systems, 10(1), 243-255.
21. Terceño, A, Brotons, J.M. y Trigueros, J.A. (2007a). El saneamiento
de las aguas residuales y sus
costes. Una propuesta de financiación. Revista Iberoamericana
de Contabilidad de Gestión, 9(5),
185-208.
22. Terceño, A, Brotons, J.M. y Trigueros, J.A. (2007b). Propuesta de un
modelo integral de financiación
de las empresas depuradoras de
aguas residuales. Actualidad Contable Faces, 10(15), 155-165.
23. Terceño, A, Brotons, J.M. y Trigueros, J.A. (2009). Evaluación de las
necesidades hídricas en España.
Ingeniería Hidráulica en México,
24(4), 7-22.
24. Wang, X. (1996). Joint products
and responses to a profit tax: the
case of endogenous cost allocation.
Public Finance Quarterly, 24(4),
494-500.
25. Zadeh, L.A. (1965). Fuzzy sets. Information and control, 8, 338-353.
26. Zimmermann, H.J. (1978). Fuzzy
programming and linear programming with several objective functions. Fuzzy sets and systems, 1(1),
45-55.
 X a Ã
acepta valores diferentes a 0 y 1. Un
subconjunto borroso à puede ser definido como à = {x, μà (x)/x
X a Ã
acepta valores diferentes a 0 y 1. Un
subconjunto borroso à puede ser definido como à = {x, μà (x)/x  X} donde μà (x)
se denomina función de pertenencia
y es una aplicación μà (x)
X} donde μà (x)
se denomina función de pertenencia
y es una aplicación μà (x) [0,1] . Un α
-corte es un conjunto ordinario (crisp)
que contiene elementos cuyo nivel de
pertenencia es al menos α. Para un
subconjunto borroso Ã, se denotará
un α -corte con Ãα siendo su expresión
matemática:
[0,1] . Un α
-corte es un conjunto ordinario (crisp)
que contiene elementos cuyo nivel de
pertenencia es al menos α. Para un
subconjunto borroso Ã, se denotará
un α -corte con Ãα siendo su expresión
matemática: 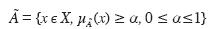
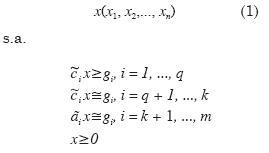
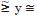 indican que
las ecuaciones o inecuaciones son flexibles y que tienen una interpretación
del tipo "esencialmente mayor que" o
"aproximadamente igual que", respectivamente. De acuerdo con Rommel-fanger y Slowinski (1998) se puede
interpretar la restricción
indican que
las ecuaciones o inecuaciones son flexibles y que tienen una interpretación
del tipo "esencialmente mayor que" o
"aproximadamente igual que", respectivamente. De acuerdo con Rommel-fanger y Slowinski (1998) se puede
interpretar la restricción 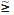 como:
como: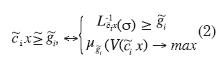
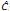 ix se denota por
cix . La función de pertenencia puede
expresarse:
ix se denota por
cix . La función de pertenencia puede
expresarse: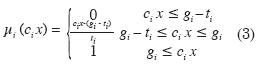
 es similar.
es similar. 
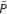 A(Pa, Pb, Pc), donde Pa es el mínimo, Pc
el máximo, y Pb el valor más posible,
siendo sus α -cortes
A(Pa, Pb, Pc), donde Pa es el mínimo, Pc
el máximo, y Pb el valor más posible,
siendo sus α -cortes  i) serán el cociente en el punto de separación entre el valor del producto i y el del total de la producción.
A modo de ejemplo, el coeficiente de
reparto de costes asignados al agua
depurada es
i) serán el cociente en el punto de separación entre el valor del producto i y el del total de la producción.
A modo de ejemplo, el coeficiente de
reparto de costes asignados al agua
depurada es 

 , y la
función de eficiencia de dicho proceso j será,
, y la
función de eficiencia de dicho proceso j será, 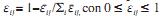 1,
para el conjunto de la EDAR, si
a cada sección se le asigna una
importancia ωj tal que ∑jωj = 1,
la función de ineficiencia será
1,
para el conjunto de la EDAR, si
a cada sección se le asigna una
importancia ωj tal que ∑jωj = 1,
la función de ineficiencia será 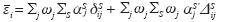
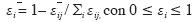

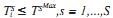 . Por su parte,
el porcentaje de reducción total de la
depuradora i para el parámetro s (PSi)
deberá ser superior al valor mínimo
(PSmin) y no se aceptan violaciones de
las mismas,
. Por su parte,
el porcentaje de reducción total de la
depuradora i para el parámetro s (PSi)
deberá ser superior al valor mínimo
(PSmin) y no se aceptan violaciones de
las mismas, 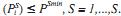
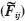
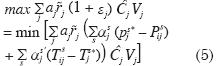
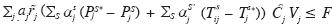 . En este tipo de
objetivos (restricciones), resulta muy
complejo definir un valor máximo que
no se pueda sobrepasar por lo que
resulta muy aconsejable considerar
una restricción con un cierto grado
de imprecisión (borrosa).
. En este tipo de
objetivos (restricciones), resulta muy
complejo definir un valor máximo que
no se pueda sobrepasar por lo que
resulta muy aconsejable considerar
una restricción con un cierto grado
de imprecisión (borrosa).
 Sj (en la medida
que mejore la información sobre
dicho consumo el número borroso
considerado irá perdiendo vaguedad hasta convertirse en un número
crisp) con un precio ES, siendo el
nivel E la meta que la empresa se
plantea no sobrepasar:
Sj (en la medida
que mejore la información sobre
dicho consumo el número borroso
considerado irá perdiendo vaguedad hasta convertirse en un número
crisp) con un precio ES, siendo el
nivel E la meta que la empresa se
plantea no sobrepasar: 

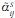 a
las unidades de reactivo S utilizadas por la EDAR i para mejorar
la concentración en una unidad
porcentual en el proceso j, que
se asumirán borrosas por ciertas
carencias de información a la implantación del presente modelo,
siendo su precio RS y R el coste que
no deberá sobrepasar:
a
las unidades de reactivo S utilizadas por la EDAR i para mejorar
la concentración en una unidad
porcentual en el proceso j, que
se asumirán borrosas por ciertas
carencias de información a la implantación del presente modelo,
siendo su precio RS y R el coste que
no deberá sobrepasar: 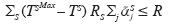
 Sj)
de la EDAR, fijándose una meta:
Sj)
de la EDAR, fijándose una meta: 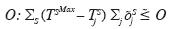
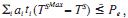 siendo ti el número de días en que no
se alcanzan los mínimos requeridos.
En el entorno de la decisión fuzzy, el
objetivo es maximizar cada una de
las funciones de pertenencia asociadas a cada uno de los objetivos. Se
denotará por tF, tE, tP, tR, tO y tPe, los límites de tolerancia correspondientes
a los niveles de aspiración F, E, P, R,
O y Pe; por KSj, HSj, ASj, OSj , los valores
centrales de los números borrosos
siendo ti el número de días en que no
se alcanzan los mínimos requeridos.
En el entorno de la decisión fuzzy, el
objetivo es maximizar cada una de
las funciones de pertenencia asociadas a cada uno de los objetivos. Se
denotará por tF, tE, tP, tR, tO y tPe, los límites de tolerancia correspondientes
a los niveles de aspiración F, E, P, R,
O y Pe; por KSj, HSj, ASj, OSj , los valores
centrales de los números borrosos
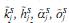 y por Z la función objetivo
donde PTI,..., PTS PPI,..., PPS , PF, PC y PPe
representan los niveles de prioridad,
que presentan la siguiente relación:
PTI »... »... PTS » PPI »...» PPS » PF » PC »
PPe » i = 1 ... S.
y por Z la función objetivo
donde PTI,..., PTS PPI,..., PPS , PF, PC y PPe
representan los niveles de prioridad,
que presentan la siguiente relación:
PTI »... »... PTS » PPI »...» PPS » PF » PC »
PPe » i = 1 ... S.