LA TASA DE INTERÉS: INFORMACIÓN CON ESTRUCTURA
GUILLERMO BUENAVENTURA VERA
Profesor de tiempo completo de la Universidad ICESI; Magíster en Ingeniería Industrial y Sistemas, Universidad del Valle; Magíster en Administración de Empresas; Eafit-Icesi; Especialista en Finanzas, Universidad del Valle; Ingeniero Químico, Universidad del Valle. buenver@icesi.edu.co
Fecha de recepción: 13-11-2002 Fecha de aceptación: 10-3-2003
RESUMEN
Partiendo de la naturaleza de la tasa de interés se describen las diferentes formas de nombrarla y se emplea el concepto de equivalencia del valor del dinero en el tiempo, para desarrollar los modelos de conversión de tasas. El tratamiento deductivo es riguroso, pero se ejemplifica cada caso.
Se hace una presentación estructurada del desarrollo, al punto de establecer un procedimiento nemotécnico para abordar en forma sencilla la secuencia de modelos y fórmulas de conversión.
Finalmente se presenta una forma alterna de nominación de las tasas y su equivalencia con la correspondiente al desarrollo del artículo.
PALABRAS CLAVES
Equivalencia, valor del dinero en el tiempo.
Clasificación: B
ABSTRACT
Interest rate can be expressed in different forms. In this paper, the concept of equivalence in the time money value theory is applied to develop the relationships between the different forms of expressing interest rates, including anticipated interest rates. A visual procedure is included to follow the appropiate set of convertion formulas.
There is not a standard mode to denote each form of interest rate. The treatment in the paper is based on the classical system to denote forms of interest rates, but the equivalence with an alternative system, the commercial forms, is showed additionally.
KEY WORDS
Time Money Value, Equivalence, Interest rate.
1. INTRODUCCIÓN
Poder comparar entre sí tasas de diferentes nominaciones, tener la posibilidad de entender la información pública sobre tasas de interés, estar en capacidad plena de tomar decisiones sobre alternativas de financiación y aun de inversión, son posibilidades que se tienen a través de la cabal interpretación y la habilidad de manejo de las tasas de interés.
En esta presentación se busca la claridad conceptual del tema fundamentada en los procedimientos de conversión de tasas de interés. El artículo basa su tratamiento matemático en el concepto de equivalencia del valor del dinero en el tiempo, el cual establece que un monto de dinero no conserva su valor a lo largo del tiempo, pero que, involucrando apropiadamente una tasa de interés, se hace posible calcular los montos equivalentes a él en todo momento. Basado en este desarrollo se establecen las relaciones matemáticas entre las diferentes denominaciones de la tasa de interés.
Adicionalmente se desarrolla la ruta de equivalencia de tasas como un método nemotécnico de aplicación. Los procedimientos establecidos enfocan el manejo de modelos mediante la calculadora científica, lo que representa la condición más demandante pero más sólida de comprensión, condición también necesaria para la utilización amplia y certera de la calculadora financiera. Sin embargo, el manejo de una calculadora financiera se ve mucho mejor asistido cuando se conecta conceptualmente con el enfoque que se presenta en el documento, ya que es éste precisamente el que subyace en sus algoritmos.
2. MANEJO DE LAS TASAS DE INTERÉS
2.1 Concepto de tasa de interés
La tasa de interés representa el importe del alquiler del dinero. Dado que los montos de intereses son dinero lo mismo que el capital, este importe se presenta normalmente como un porcentaje que se aplica al capital por unidad de tiempo; a este valor se le denomina tasa de interés.
Para poder aplicar las fórmulas de equivalencia de cifras de dinero en el tiempo, es necesario que la base del tiempo para la tasa de interés aplicada coincida con el período o longitud del intervalo de la línea del tiempo entre momentos consecutivos. A esta presentación de la información del interés se le llama tasa periódica.
El período puede ser finito (día, mes, bimestre, trimestre, semestre, año, etc.) o infinitesimal (cuando tiende a cero), en cuyo caso el tratamiento toma el nombre de interés continuo, y es asistido por una serie de formulaciones que no se tratarán en este documento por considerarlo un tema muy especializado y de poca utilización en nuestro medio.
Además de contar con la información del interés en tasas periódicas se pueden manejar otras formas, como la tasa nominal y la tasa efectiva, las cuales se discuten enseguida.
2.2 Naturaleza de las tasas de interés
La declaración de una tasa de interés lleva implícitos dos elementos:
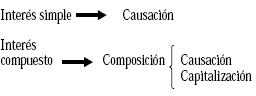
Causación: Informa el momento en el cual el interés se causa o tiene lugar según se haya estipulado en el contrato o por el negocio en cuestión. Aquí el monto de interés se calcula y se da por cierto, pero no necesariamente se cancela sino que se puede acumular aditivamente (interés simple, si se acumula sin capitalizarse) o se puede capitalizar (interés compuesto).
Capitalización: Informa el momento en el cual el interés calculado o acumulado aditivamente se lleva a capital, o sea, se capitaliza.
Rigurosamente no tiene que existir coincidencia entre los períodos de causación y de capitalización (puede pensarse, por ejemplo, en una tasa de interés del 2% mensual capitalizable trimestralmente); sin embargo, y tal vez por lo imprácticos que se tornarían los cálculos en ese ambiente, se tiene prácticamente en la totalidad de las situaciones una coincidencia de los dos períodos, en cuyo caso se le denomina período de composición:
Componer = Causar y Capitalizar
Nótese que en el caso de interés simple no hay capitalización y por lo tanto no hay composición, sólo existe causación. El interés compuesto, por el contrario, se construye sobre el concepto de composición:

Aún hay más consideraciones; desde el ángulo de la causación, el interés puede exigirse al vencimiento o anticipadamente, según se estipule en el contrato (así como el canon de arrendamiento se acostumbra cobrar anticipadamente o el salario se acostumbra pagar al vencimiento del período), con lo que se puede resumir la naturaleza del interés en el siguiente esquema:
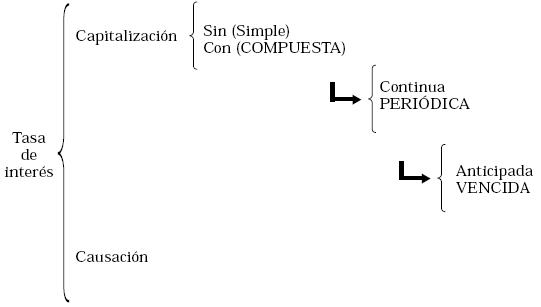
En la práctica, los modos que se presentan con letras mayúsculas en el esquema anterior son clásicos y se entienden "por defecto"; es decir, si una tasa no se declara simple se entiende COMPUESTA; si no se declara continua se entiende PERIÓDICA; si no se declara anticipada se entiende VENCIDA.
2.3 Denominaciones de la tasa de interés
Según la manera como una tasa de interés proponga la información se le denomina de una de estas tres maneras:
Periódica: La tasa corresponde al período de composición (% por día, mes, bimestre, trimestre, semestre, año, etc.). Algunos sectores la conocen como tasa efectiva periódica (efectiva diaria, efectiva mensual, efectiva trimestral, etc.), pero aquí se denominará simplemente tasa periódica.
Nominal: Es la expresión anualizada de la tasa periódica, contabilizada por acumulación simple de ella.
Efectiva: Es la expresión equivalente de una tasa periódica en la que el período se hace igual a un año y la causación siempre se da al vencimiento. Algunos sectores emplean el nombre de tasa efectiva para aplicarla a un período distinto del año (efectiva diaria, efectiva mensual, efectiva trimestral, etc.), pero aquí no se empleará esta denominación, la cual la llamaremos simplemente tasa periódica. La tasa efectiva se conoce también como tasa efectiva anual, tasa anual efectiva o aun tasa anual.
dicionalmente, como ya se indicó, la tasa debe definir la forma en que se causa el interés:
Anticipada: Cuando el interés se causa en forma anticipada en el período. Cabe anotar que la Tasa Efectiva no puede darse, por definición, en forma anticipada, es decir no existe una tasa efectiva anticipada.
Vencida: Cuando el interés se causa en forma vencida en el período. Cabe anotar que la tasa efectiva es siempre vencida y por lo tanto esta última palabra se omite en su declaración.
2.4 Clases de tasas de interés
De acuerdo con lo tratado en el numeral anterior, se pueden emplear cinco clases de tasa de interés:
En resumen, la notación de estas clases de tasas para efectos de la exposición en este documento es la siguiente:
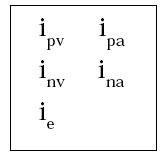
ipv = Tasa de interés periódico vencido (% por período vencido)
ipa = Tasa de interés periódico anticipado (% por período anticipado)
inv = Tasa de interés nominal vencido (% anual, compuesto por período vencido)
ina = Tasa de interés nominal anticipado (% anual, compuesto por período anticipado)
ie = Tasa de interés efectivo (% anual efectivo)
2.5 Declaración de las tasas de interés
Cuando se lee una tasa de interés, normalmente no se encuentra expresada con palabras la modalidad de la cual se trata; ésta se obtiene de la información que acompaña a las cifras de porcentaje, usualmente en siglas.
Ejemplo: 30% a.m.v. representa una tasa de interés del 30% anual compuesto mensualmente y causada al vencimiento de cada período.
La información se estructura en Campos y en Siglas siguiendo al signo de porcentaje (%):
2.5.1 Campos
Tasas nominales
El primer campo siempre tendrá una a o la palabra anual, estableciendo que es una tasa anualizada.
El segundo campo lleva la sigla o la palabra correspondiente al período de composición (por ejemplo m o mensual, significando que el período de composición corresponde al mes).
El tercer campo contiene la información correspondiente al momento de causación del interés; llevará una a (o la palabra anticipado) si el interés es anticipado, o una v (o la palabra vencido), o simplemente se deja vacío (información "por defecto") si el interés es vencido.
Tasas periódicas
No llevan el primer campo de las tasas nominales, o sea, no tienen la sigla a o la palabra anual siguiendo al signo de porcentaje (%), porque no son tasas anualizadas. Los dos campos subsiguientes tienen la misma connotación de los campos segundo y tercero de las tasas nominales.
Tasa efectiva
Se reconoce que una tasa es efectiva cuando sólo tiene una de estas siglas: e.a., a.e., a., e.
Ejemplo: Son declaraciones de tasas efectivas anuales:
23% a.e.
20% a.
30% e.a.
28% e.
2.5.2 Siglas
Tasa efectiva
Una tasa se denota efectiva si después del signo de porcentaje lleva una de estas siglas:
e.a.
a.e.
e. solamente
a. solamente
Tasas nominales y periódicas
Una tasa es nominal o es periódica si se determina con siglas diferentes a las consignadas inmediatamente antes.
Primer campo:
a. = significa que la tasa es anualizada (nominal).
anual = significa que la tasa es anualizada (nominal).
Otra sigla = significa que la tasa es periódica.
Segundo campo (o primer campo, si la tasa es periódica, es decir no lleva la sigla de anualización): Determina el período de composición:
d. = diario
m. = mensual
b. = bimestral
t. = trimestral
s. = semestral
a. = anual
día = diario
mes = mensual
bimestre = bimestral
trimestre = trimestral
semestre = semestral
anual = anual
Tercer campo (o segundo campo, si la tasa es periódica, es decir no lleva sigla de anualización). Determina el modo de causación:
a. = anticipadamente
v. = al vencimiento
Si se omite = al vencimiento
Ejemplo:
22% e.a. significa 22% efectiva anual
23% a.m.v. significa 23% anual mes vencido
24% a.b.a. significa 24% anual bimestre anticipado
25% a.s. significa 25% anual semestre vencido
6% t.v. significa 6% trimestral vencido
2% m.a. significa 2% mensual anticipado
2.6 Equivalencia de las tasas de interés
2.6.1 Tasa periódica y tasa nominal
Como una herencia de tratamiento en interés simple, y coincidiendo con él, la tasa nominal en el contexto de interés compuesto representa la anualización de la tasa periódica por acumulación simple de esta en cada período. Por lo tanto, la tasa nominal se obtiene multiplicando la tasa periódica por el respectivo número de períodos contenidos en el año; si la tasa periódica es anticipada, la tasa nominal también lo será, y viceversa; y si la tasa periódica es vencida, la tasa nominal también lo será, y viceversa:
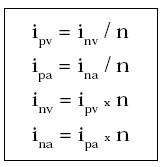
ipv: Tasa de interés periódica vencida (% por día, mes, etc.)
inv: Tasa de interés nominal vencida (% anual)
ipa: Tasa de interés periódica anticipada (% por día, mes, etc.)
ina: Tasa de interés nominal anticipada (% anual)
n: Número de períodos por año (360 días, 12 meses, etc.)
Ejemplo: Encontrar la tasa periódica correspondiente a una tasa nominal del 24% a.m.v.:
inv = 24% a.m.v. n = 12 meses por año
ipv = 24% / 12 = 2% m.v.
Ejemplo: Encontrar la tasa nominal correspondiente a una tasa periódica del 10% s.a.:
ipa = 10% s.a.
n = 2 semestres por año
ina = 10% x 2 = 20% a.s.a.
2.6.2 Tasa vencida y tasa anticipada
En la modalidad de interés anticipado, el monto de intereses se paga o se capitaliza al comienzo del período. Para encontrar la equivalencia con el interés vencido se emplea la noción de equivalencia entre un flujo presente y un flujo futuro para un período, como sigue:
P = X - ipa X
P = X (1-ipa)
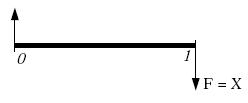
La tasa de interés aparece como un descuento al monto del flujo presente, y por lo tanto no tiene por qué aparecer al final.
Aplicando el concepto de equivalencia se tiene:
F = P (1+ipv)
Reemplazando por las expresiones de F y de P:
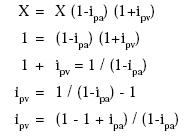
O sea,
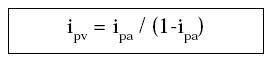
ipv: Tasa de interés periódica vencida (% por día, mes, etc.)
ipa: Tasa de interés periódica anticipada (% por día, mes, etc.)
De la misma manera es posible despejar el valor de ipa:
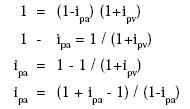
O sea,
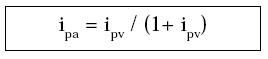
ipv: Tasa de interés periódica vencida (% por día, mes, etc.)
ipa: Tasa de interés periódica anticipada (% por día, mes, etc.)
Ejemplo: Encontrar la tasa periódica vencida equivalente a una tasa del 4% t.a.:
ipa = 4% = 0,04
ipv = 4% / (1 - 0,04) = 4,17% t.v.
Ejemplo: Encontrar la tasa periódica anticipada equivalente a una tasa del 9% s.v.:
ipv = 9% = 0,09
ipa = 9% / (1 + 0,09) = 8,26% s.a.
Cabe anotar que la equivalencia entre tasas anticipada y vencida sólo se da para tasas periódicas. De hecho la tasa nominal sólo sirve para encontrar la respectiva tasa periódica y no puede ser operada directamente con el concepto de equivalencia.
2.6.3 Tasa efectiva y tasa periódica
La tasa efectiva representa una tasa periódica vencida en la cual el período es exactamente un año. Para desarrollar la equivalencia entre la tasa efectiva y la tasa periódica se supone que un año consta de n períodos:
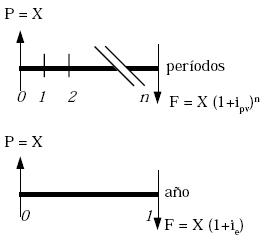
Con la misma inversión P = X, al cabo de un año se debe tener la misma cantidad de dinero F en los dos planes presentados en el dibujo de flechas:
X (1+ipv)n = X (1+ie)
1 + ie = (1 + ipv)n
Despejando ie se tiene:
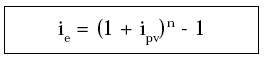
ie: Tasa efectiva de interés (% anual)
ipv: Tasa de interés periódica vencida (% por día, mes, etc.)
Despejando ipv se tiene:
ie:Tasa efectiva de interés (% anual)
ipv: Tasa de interés periódica vencida (% por día, mes, etc.)
Ejemplo: ¿Cuál es la tasa efectiva anual correspondiente a una tasa del 2% mensual?
ipv = 2% mensual = 0,02
n = 12 meses / año
ie = (1 + 0,02)12 - 1 = 0,26824 = 26,82% e.a.
Ejemplo: ¿Cuál es la tasa trimestral correspondiente a una tasa del 24% e.a.?
ie = 24 % e.a. = 0,24
n = 4 trimestres / año
ipv = (1 + 0,24)1/4 - 1 = 0,05525 = 5,53% t.v.
3. LA RUTA DE EQUIVALENCIA DE TASAS
Aunque pueden derivarse más ecuaciones de relación, las formulaciones anteriores de equivalencia de tasas se consideran fundamentales y dan lugar a la Ruta de Equivalencia de Tasas®, la cual constituye una herramienta nemotécnica para realizar conversión de cualquier clase de tasa de interés a cualquiera otra de una manera sencilla:
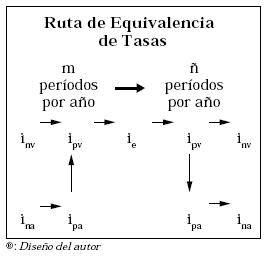
Ejemplo: Encontrar la tasa nominal mes vencido equivalente a una tasa del 30% a.s.a.:
ina = 30% a.s.a.
m = 2 semestres / año
ñ = 12 meses / año
ipn = ?
Con m = 2 se pasa de una tasa nominal a una tasa efectiva, atendiendo a la ruta de equivalencia de tasas y de acuerdo con las fórmulas desarrolladas:
ipa = 30% / 2 = 15% s.a.
ipv = 15% / (1-0,15) = 17,65% s.v.
ie = (1+0,1765)2 - 1 = 38,41% e.a.
Ahora, con ñ = 12 se pasa de la tasa efectiva a la correspondiente tasa nominal vencida:
ipv = (1+0,3841)1/12 - 1 = 2,75% m.v.
inv = 2,75 x 12 = 32,95% a.m.v.
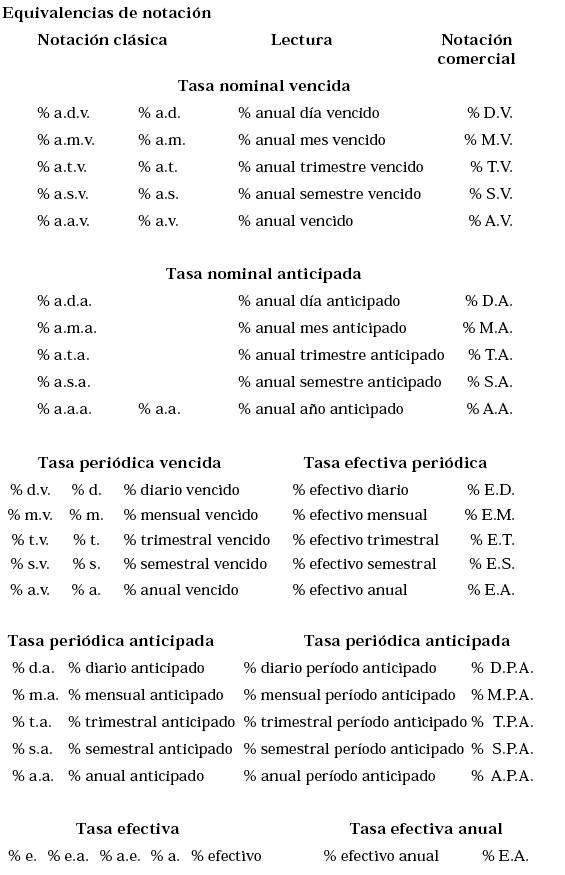
4. ANEXO: TASAS DE INTERÉS: NOTACIÓN COMERCIAL
Presentación
Como se pudo observar, la declaración del modo de una tasa de interés se tiene mediante la lectura de las siglas que suceden al signo de porcentaje (%). La notación presentada hasta ahora no es la única. Una notación muy utilizada en publicaciones de prensa y en anuncios comerciales es la que se expone a continuación:
Nominal (anualizada)
Efectiva (periódica).
En lugar de los tres tipos de tasa tradicionales:
Nominal (anualizada).
Efectiva (anual).
Periódica.
BIBLIOGRAFÍA
Álvarez A. Matemáticas Financieras. Segunda edición, Colombia: McGraw Hill. 1999.
Brealey R., Myers S., Marcus A. Fundamentos de Finanzas Corporativas. Madrid: McGraw Hill. 1996.
Buenaventura G. Matemáticas Financieras. Segunda edición; Cali: Universidad ICESI. 2001.
García J. Matemáticas Financieras con ecuaciones de diferencia finita. Cuarta edición, Bogotá: Pearson. 2000.
Gitman L. Principles of Managerial Finance. Ninth Edition, Boston: Addison Wesley Longman. 2000.
Linero G. Matemáticas Financieras Aplicadas. Cali: Artes Gráficas Univalle. 1999.
Villalobos J. L. Matemáticas Financieras. Segunda edición; México: Prentice Hall. 2001.